Презентация на тему: Преобразование графиков функций

Преобразование графиков функций

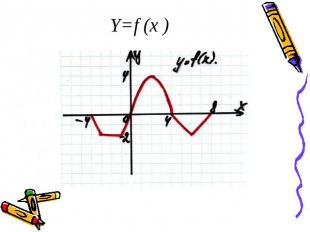
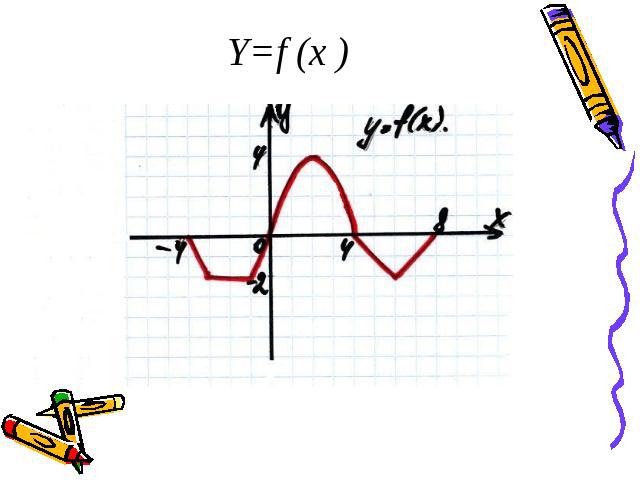
Y=f (x )

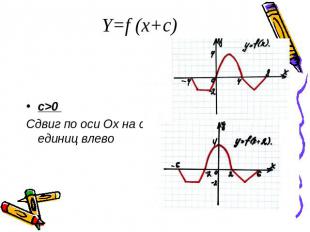
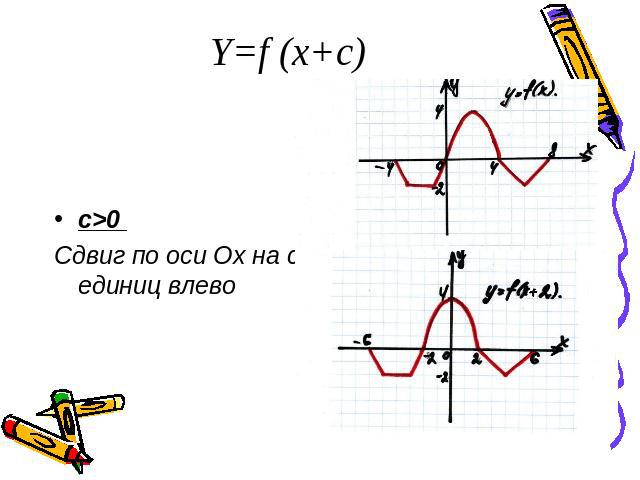
Y=f (x+c)c>0 Сдвиг по оси Ох на с единиц влево

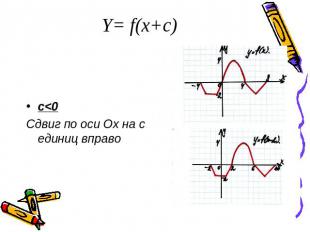
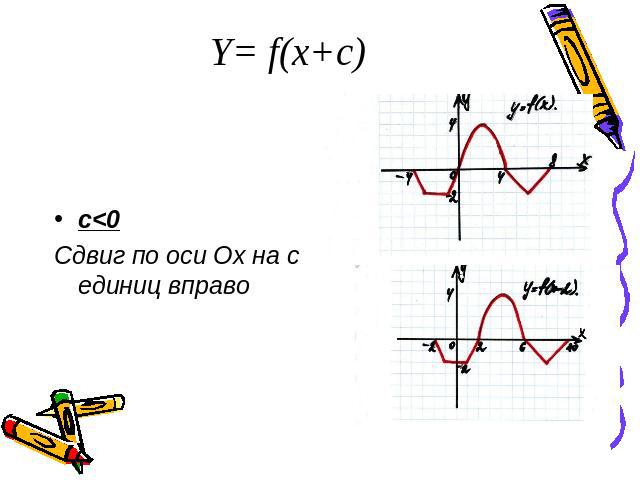
Y= f(x+c)c<0Сдвиг по оси Ох на с единиц вправо

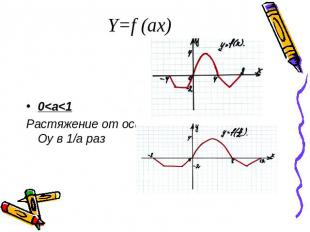
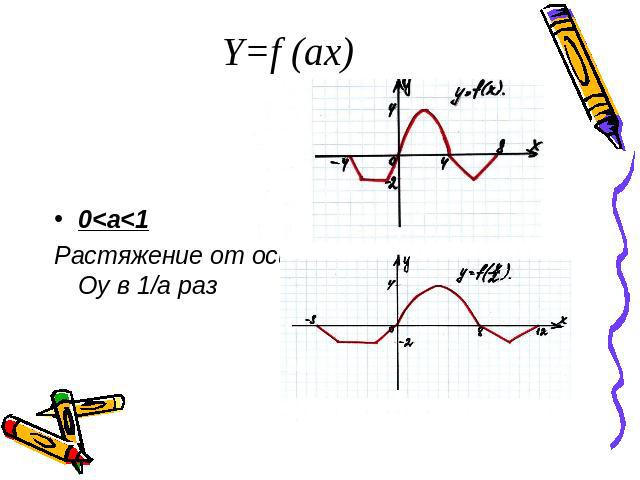
Y=f (ax)0<a<1Растяжение от оси Оу в 1/а раз

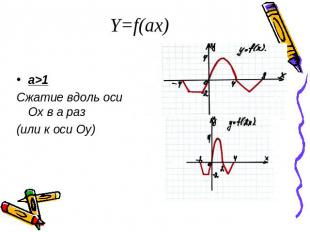
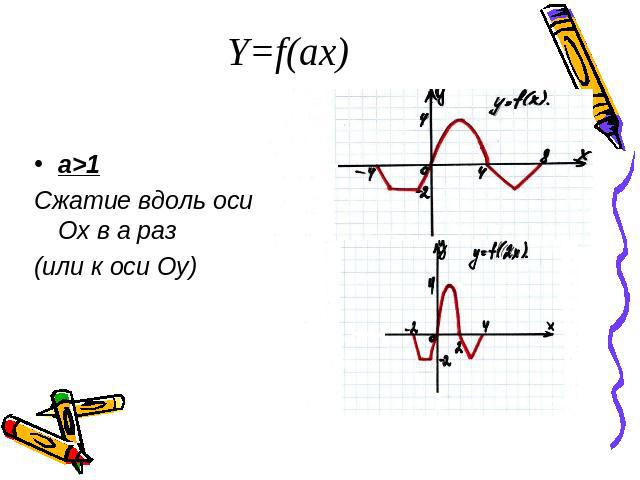
Y=f(ax)a>1Сжатие вдоль оси Ох в а раз(или к оси Оу)

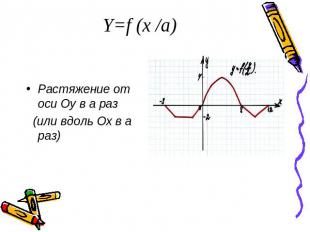
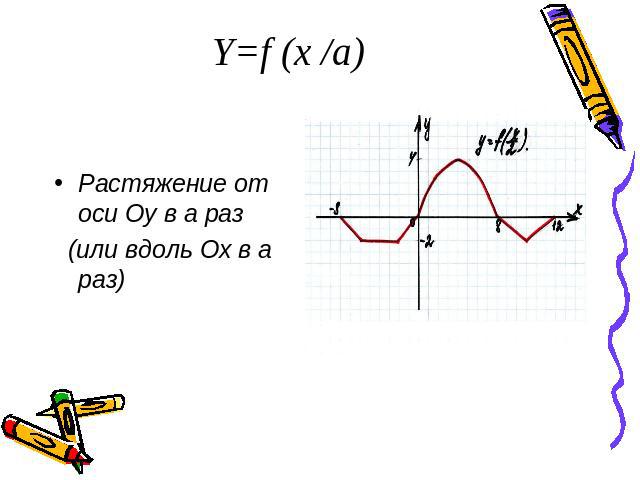
Y=f (x /a)Растяжение от оси Оу в а раз (или вдоль Ох в а раз)

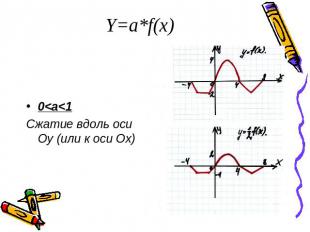
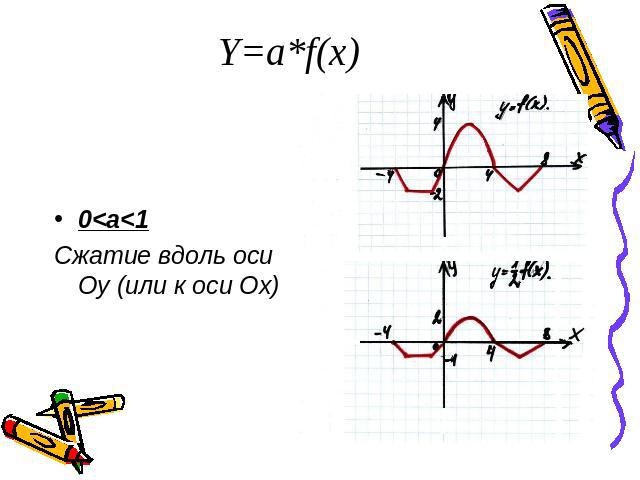
Y=a*f(x)0<a<1Сжатие вдоль оси Оу (или к оси Ох)

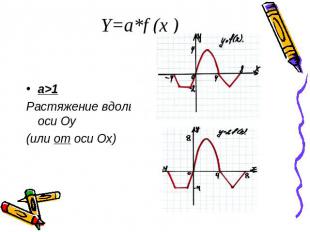
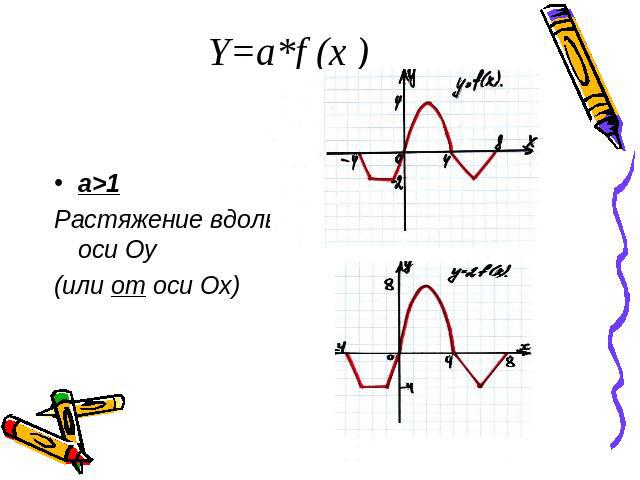
Y=a*f (x )a>1Растяжение вдоль оси Оу (или от оси Ох)

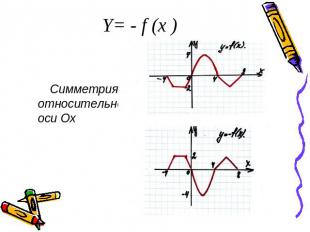
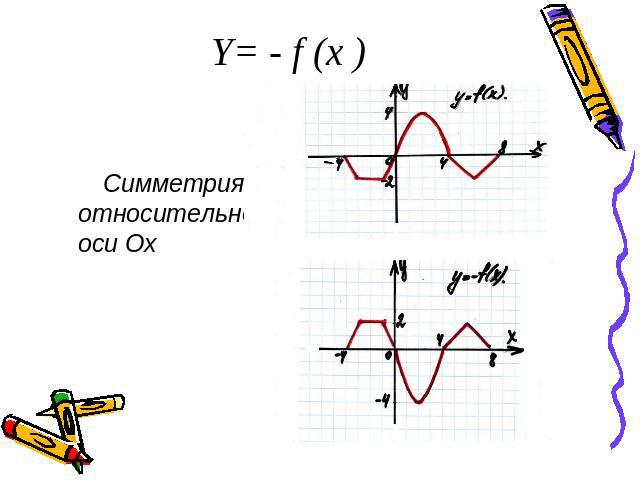
Y= - f (x ) Симметрия относительно оси Ох

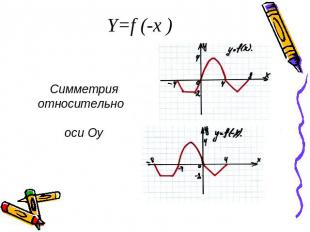
Y=f (-x ) Симметрия относительно оси Оу

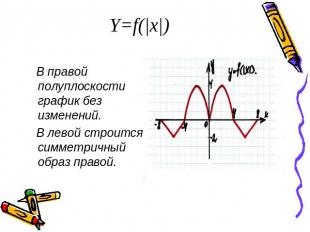
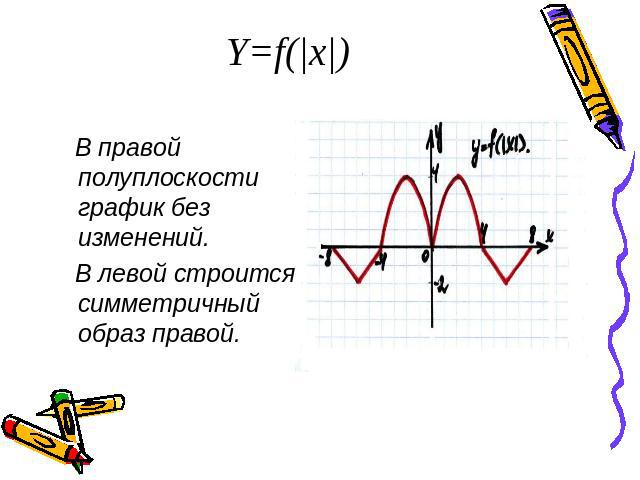
Y=f(|x|) В правой полуплоскости график без изменений. В левой строится симметричный образ правой.

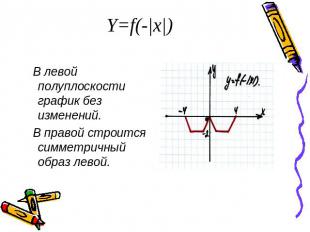
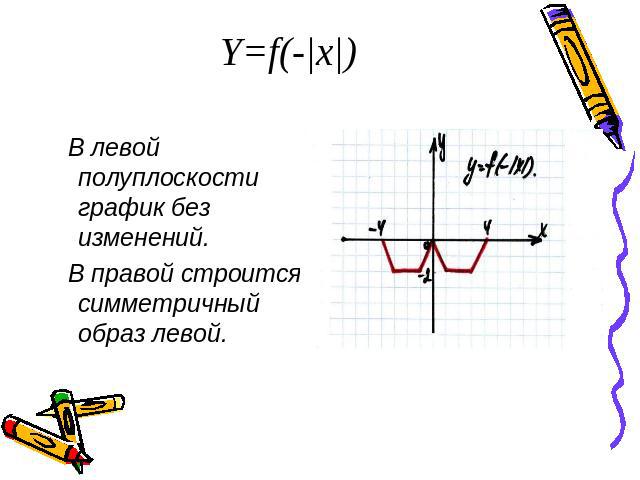
Y=f(-|x|) В левой полуплоскости график без изменений. В правой строится симметричный образ левой.

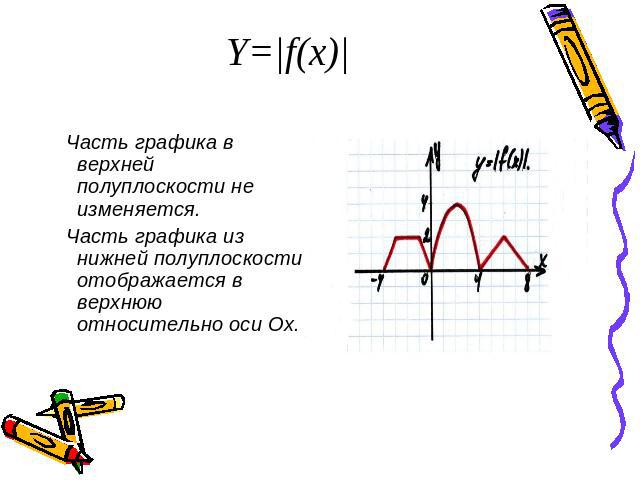
Y=|f(x)| Часть графика в верхней полуплоскости не изменяется. Часть графика из нижней полуплоскости отображается в верхнюю относительно оси Ох.

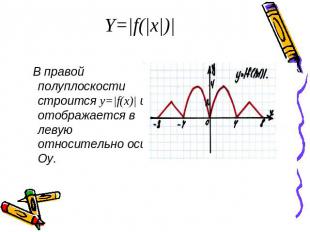
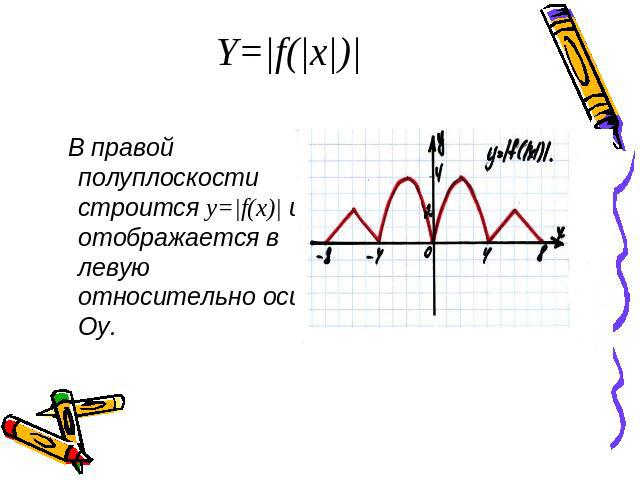
Y=|f(|x|)| В правой полуплоскости строится y=|f(x)| и отображается в левую относительно оси Оу.

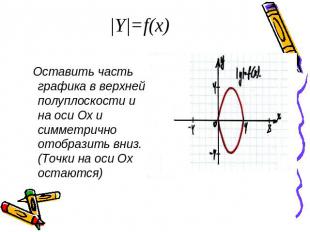
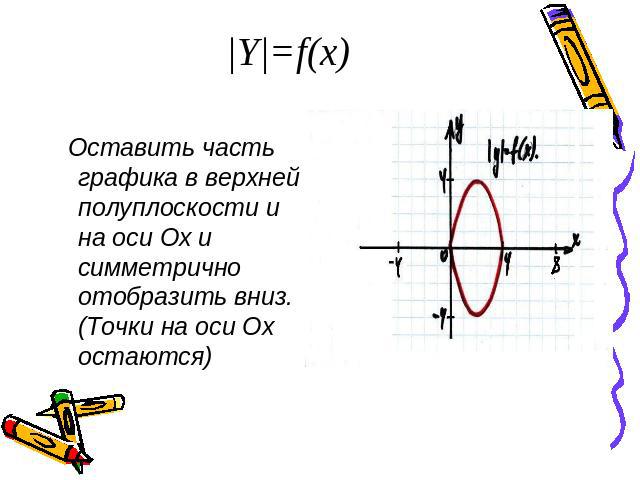
|Y|=f(x) Оставить часть графика в верхней полуплоскости и на оси Ох и симметрично отобразить вниз. (Точки на оси Ох остаются)

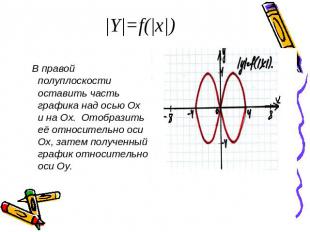
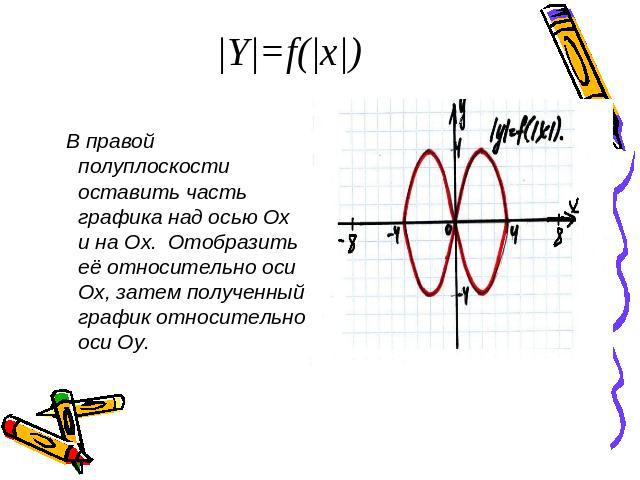
|Y|=f(|x|) В правой полуплоскости оставить часть графика над осью Ох и на Ох. Отобразить её относительно оси Ох, затем полученный график относительно оси Оу.

Конец. Забуга А. 10Б