Презентация на тему: Симметрия функций и преобразование их графиков

Симметрия функций и преобразование их графиков

Повторить определение функции; основные понятия, связанные с ней; способы задания функции. Ввести понятие чётной и нечётной функции. Освоить основные способы преобразования графиков. Воспитание интереса к математике.Развитие зрительного восприятия предмета.

1.Повторение Определение функции.Способы задания функции2.Преобразование графиков функцииСимметрия относительно оси у, f(x)→ f(- x)Симметрия относительно оси х, f(x)→ - f(x) Параллельный перенос вдоль оси х, f(x)→f(x-а)Параллельный перенос вдоль оси у,f(x) → f(x)+bСжатие и растяжение вдоль оси х, f(x) → f(αx), α>0Сжатие и растяжение вдоль оси у, f(x) → kf(x),k>0Построение графика функции у = | f (x) |Построение графика функции у = f( | x | )Построение графика обратной функции

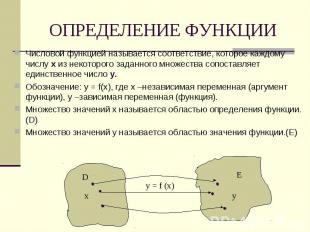
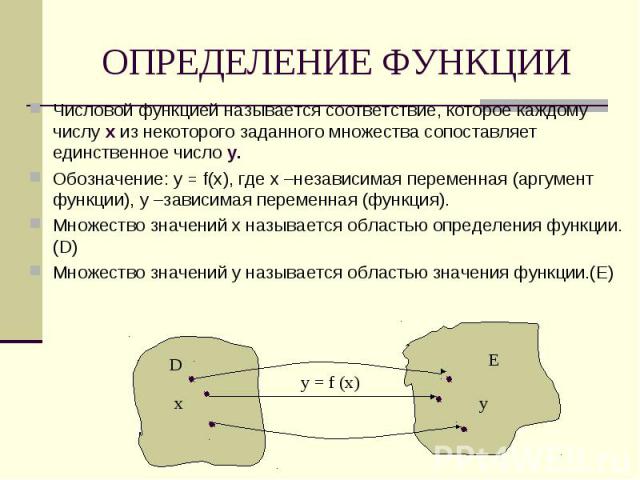
Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число у.Обозначение: у = f(х), где х –независимая переменная (аргумент функции), у –зависимая переменная (функция).Множество значений х называется областью определения функции.(D)Множество значений у называется областью значения функции.(Е)

у = √х – 2 + 3При х = 6, у(6) = √6 – 2 + 3 = 5Найдём область определения. х - 2 ≥ 0, х ≥2⇒D(у) = [2; +∞); Так как по определениюарифметического корня 0 ≤ √х – 2 ≤ +∞, 0 + 3≤ √х – 2 + 3 ≤ +∞+ 3, или 3 ≤ у ≤ +∞, Е(х) = [3; +∞)

Найти область определения и область значенияфункции f (x) = 3 + 1 . х-2Функция определена при х - 2 ≠ 0, то есть х ≠ 2⇒D(у) = (-∞;2) U (2; +∞); Так как при всех допустимых значениях х дробь 1/(х-2) не обращается в нуль, то функция f (x) принимает все значения, кроме 3. ПоэтомуЕ(f) = (-∞;3) U (3; +∞);

Найти область определения дробно-рациональнойфункции f (x) = 1 + 3 х + 4 . х-2 (х - 1)(х + 3)Знаменатели дробей обращаются в нуль при х = 2, х = 1, х = -3. Поэтому область определения D(f) = (-∞;-3) U (-3; 1) U (1; 2) U (2; +∞);

Зависимость 2 х – 3 х2 + 1Уже не является функцией. При х = 1, пользуясь верхней формулой, найдём у = 2*1 – 3 = -1, апользуясь нижней формулой, получим у = 12 + 1 = 2. Таким образом, одному значению х =1 соответствуют два значения у (у=-1 и у=2). Поэтому эта зависимость (по определению) неявляется функцией

Аналитический способ: функция задаётся с помощью формулы. Примеры: у = х2, у = ax + bТабличный способ: функция задаётся с помощью таблицы. Описательный способ: функция задаётся словесным описанием.Графический способ: функция задаётся с помощью графика.

ОПРЕДЕЛЕНИЕ ГРАФИКА ФУНКЦИИ Графиком функции называется множество точек плоскости с координатами (х; f(х))

Дана функция у = 2 х – 3 |х| + 4. Принадлежит лиграфику этой функции точка с координатами а) (-2; -6); б) (-3; - 10)Решение.а) при х = -2, у = 2· (-2) -3·|-2| + 4 = - 4 - 3·3 + 4 =-6 Так как у(-2) = -6, то точка А(-2; -6) принадлежитграфику функции.б) при х = -3, у = 2· (-3) -3·|-3| + 4 = - 6 - 3·3 + 4 =-11 Так как у(-3) = -11, то точка В(-3; -10) не принадлежитграфику функции

Дана функция f(х) = - х2 + 6х – 8. Найдём точки пересечения графика функции с осями координат.Решение.1) Точка пересечения с осью ординат, при х=0, у(0) = - 02 + 6·0 – 8 = - 8. Получаем координаты этой точки А(0; -8)2) Точка пересечения с осью абсцисс, при у =0, 0 = - х2 + 6х – 8, х2 - 6х + 8=0, D = 36 – 32 =4, x1= (6-2)/2=2,x1= (6+2)/2=4. Поэтому график функции пересекает ось абсцисс в двух точках: В(2; 0) и С(4;0)

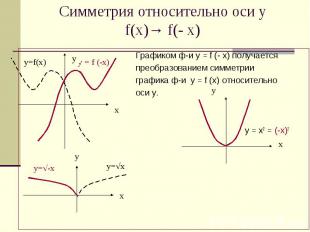
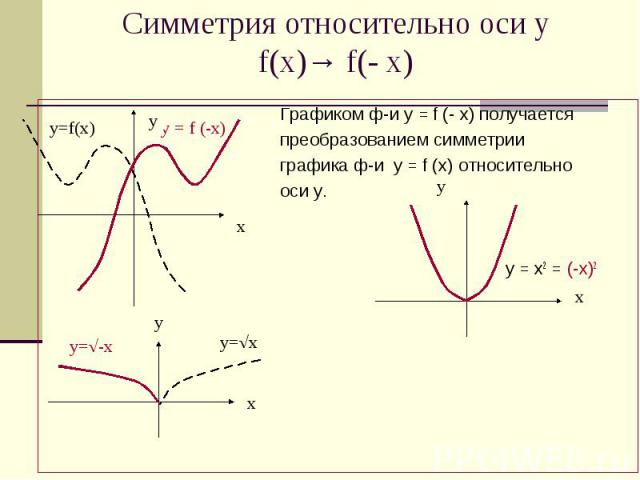
Симметрия относительно оси у f(x)→ f(- x) Графиком ф-и у = f (- х) получается преобразованием симметрии графика ф-и у = f (х) относительно оси у. у = х2 = (-х)2

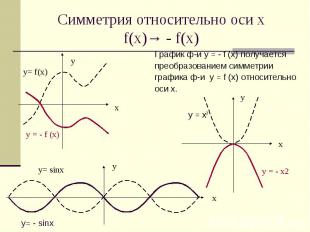
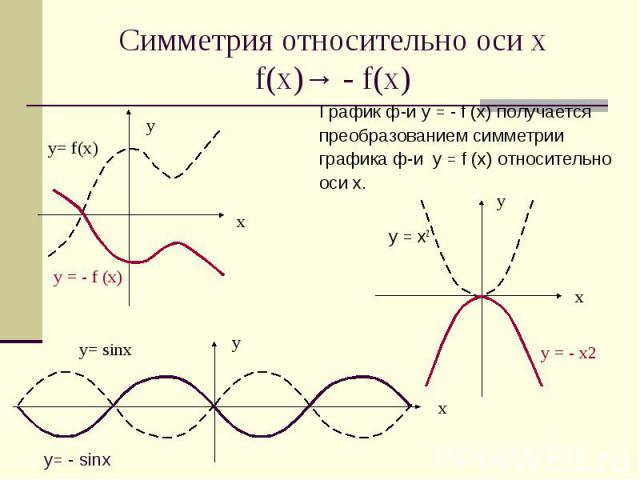
Симметрия относительно оси х f(x)→ - f(x) График ф-и у = - f (х) получается преобразованием симметрии графика ф-и у = f (х) относительно оси х. у = х2 у= - sinx

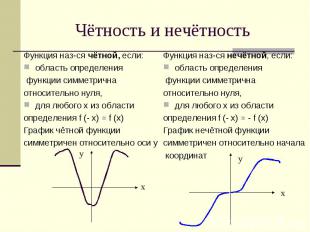
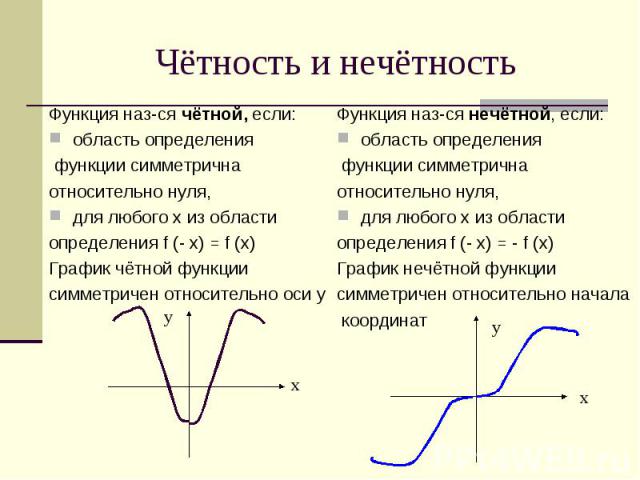
Чётность и нечётность Функция наз-ся чётной, если:область определения функции симметрична относительно нуля,для любого х из области определения f (- х) = f (х) График чётной функции симметричен относительно оси у Функция наз-ся нечётной, если:область определения функции симметрична относительно нуля,для любого х из области определения f (- х) = - f (х) График нечётной функции симметричен относительно начала координат

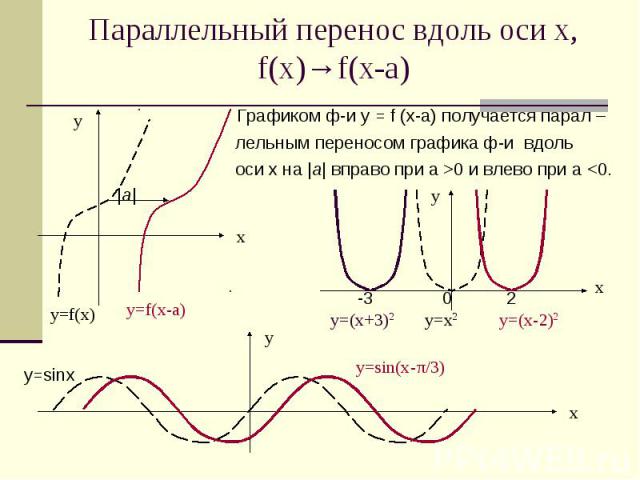
Параллельный перенос вдоль оси х, f(x)→f(x-а) Графиком ф-и у = f (х-a) получается парал – лельным переносом графика ф-и вдоль оси х на |a| вправо при а >0 и влево при а <0. |а| -3 0 2 у=sinx

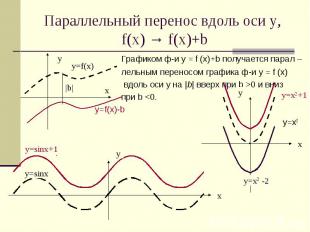
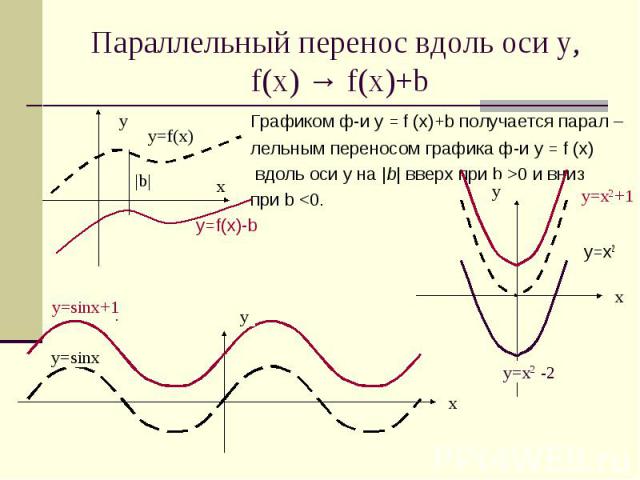
Параллельный перенос вдоль оси у, f(x) → f(x)+b Графиком ф-и у = f (х)+b получается парал – лельным переносом графика ф-и у = f (х) вдоль оси y на |b| вверх при b >0 и вниз при b <0. у=f(x)-b у=х2

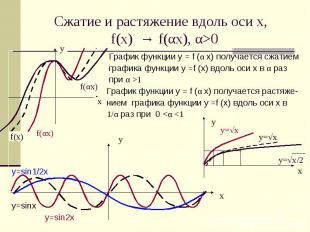
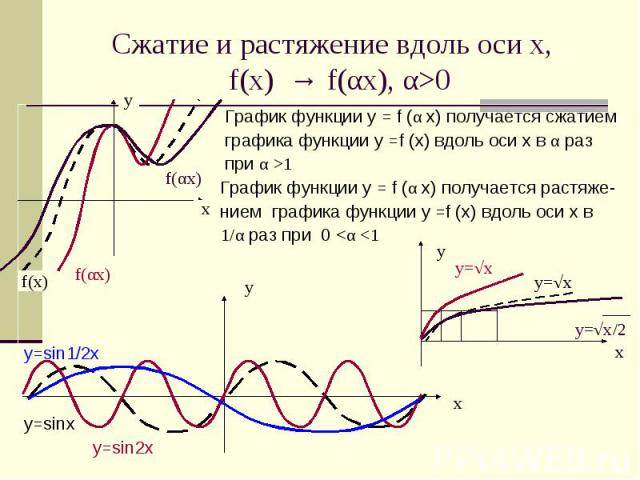
Сжатие и растяжение вдоль оси х, f(x) → f(αx), α>0 График функции у = f (α x) получается сжатием графика функции у =f (x) вдоль оси х в α раз при α >1 График функции у = f (α x) получается растяже- нием графика функции у =f (x) вдоль оси х в 1/α раз при 0 <α <1 у=√х у=√х/2у=sin1/2xу=sinx у=sin2x

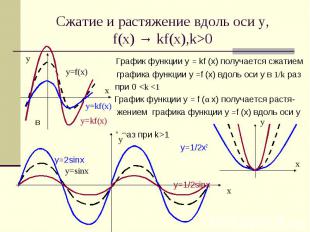
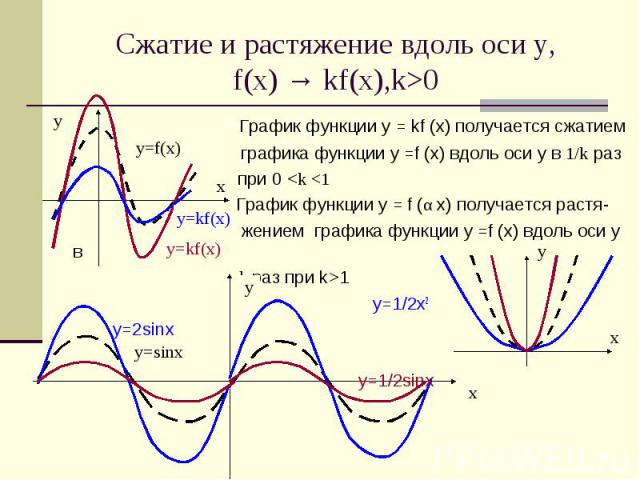
Сжатие и растяжение вдоль оси у,f(x) → kf(x),k>0 График функции у = kf (x) получается сжатием графика функции у =f (x) вдоль оси y в 1/k раз при 0 <k <1 График функции у = f (α x) получается растя- жением графика функции у =f (x) вдоль оси y в k раз при k>1 у=1/2х2 у=2sinx у=1/2sinx

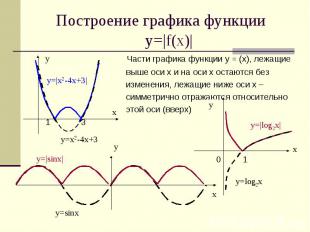
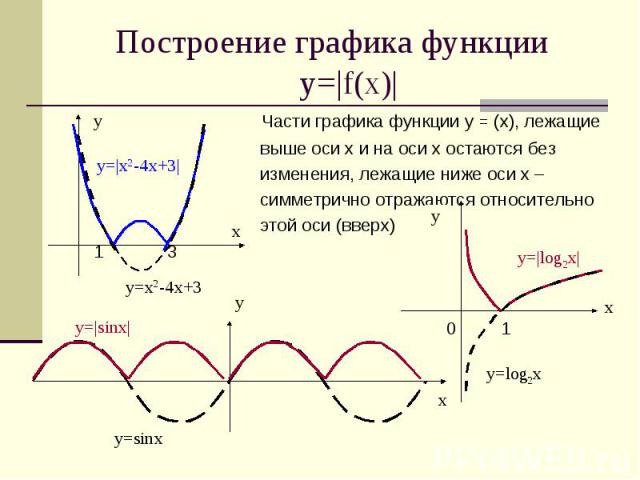
Построение графика функции у=|f(x)| Части графика функции у = (х), лежащие выше оси х и на оси х остаются без изменения, лежащие ниже оси х – симметрично отражаются относительно этой оси (вверх) 1 3 0 1

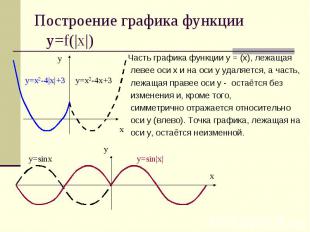
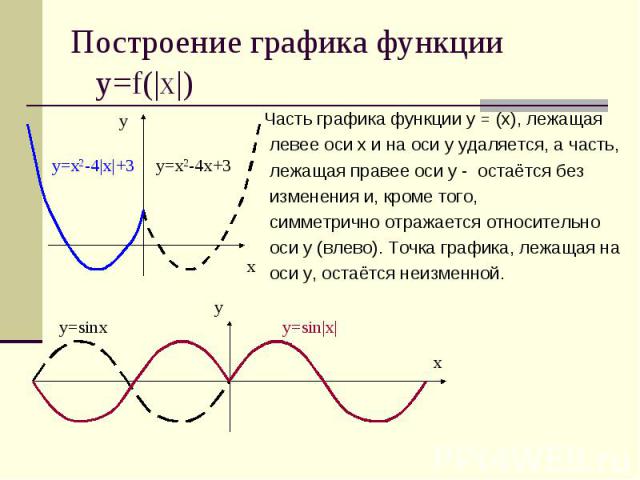
Построение графика функции у=f(|x|) Часть графика функции у = (х), лежащая левее оси х и на оси у удаляется, а часть, лежащая правее оси у - остаётся без изменения и, кроме того, симметрично отражается относительно оси у (влево). Точка графика, лежащая на оси у, остаётся неизменной.

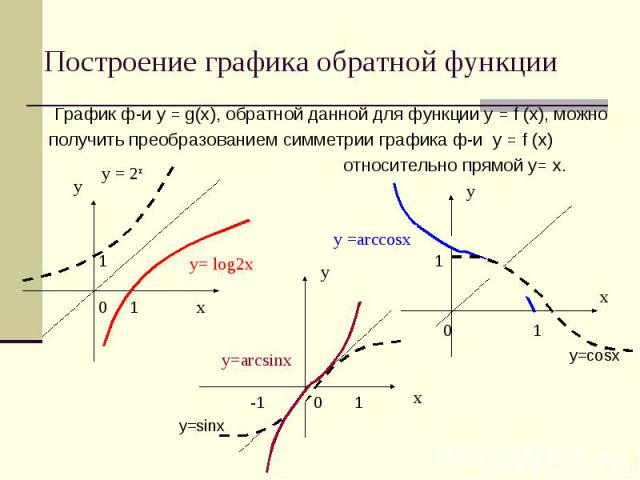
График ф-и у = g(х), обратной данной для функции у = f (х), можнополучить преобразованием симметрии графика ф-и у = f (х) относительно прямой у= х. 1 1 0 1 0 1 y=cosx -1 0 1 y=sinx

Дайте определение чётной, нечётной функций.Расскажите о способах задания функции.Что такое область определения?Что такое область значения?Как найти точки пересечения с осями координат?Какие свойства симметрии вы изучили?Как проявляются свойства симметрии на графиках?Задание на дом гл.7, занятие 4, стр. 133 – 136. Вопросы и упражнения 1- 11.