Презентация на тему: Преобразования графиков функций 10 класс

Преобразования графиков функций.Алгебра и начала анализа, 10 класс.

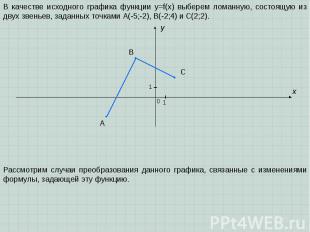
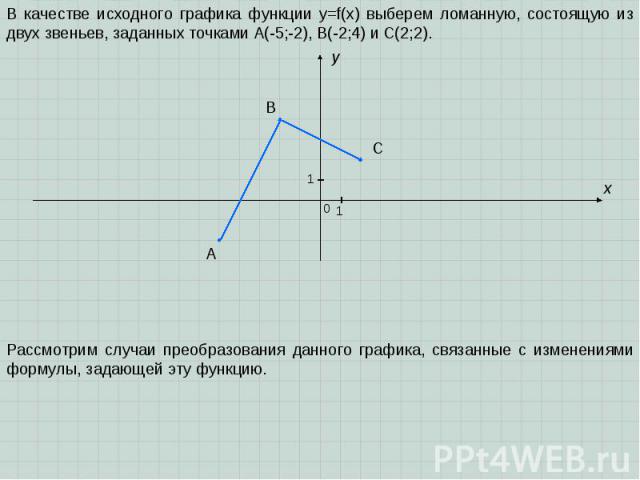
A B C x y 0 1 1 В качестве исходного графика функции y=f(x) выберем ломанную, состоящую из двух звеньев, заданных точками A(-5;-2), B(-2;4) и C(2;2). Рассмотрим случаи преобразования данного графика, связанные с изменениями формулы, задающей эту функцию.

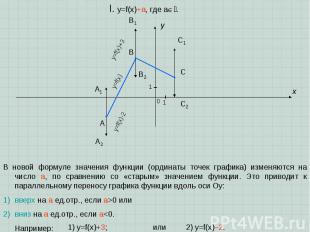
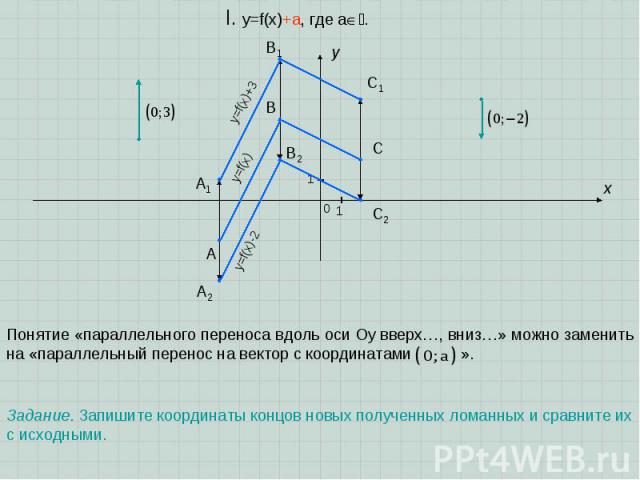
A B C x y I. y=f(x)+a, где a. 1 1 0 В новой формуле значения функции (ординаты точек графика) изменяются на число a, по сравнению со «старым» значением функции. Это приводит к параллельному переносу графика функции вдоль оси Oy: вверх на a ед.отр., если a>0 или вниз на a ед.отр., если a

A B C x y I. y=f(x)+a, где a. 1 1 0 Понятие «параллельного переноса вдоль оси Oy вверх…, вниз…» можно заменить на «параллельный перенос на вектор с координатами ». A1 B1 C1 y=f(x) y=f(x)+3 A2 B2 C2 Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными. y=f(x)-2

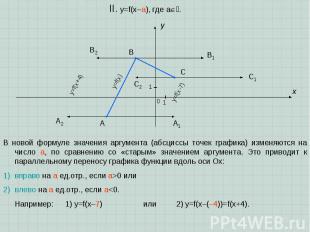
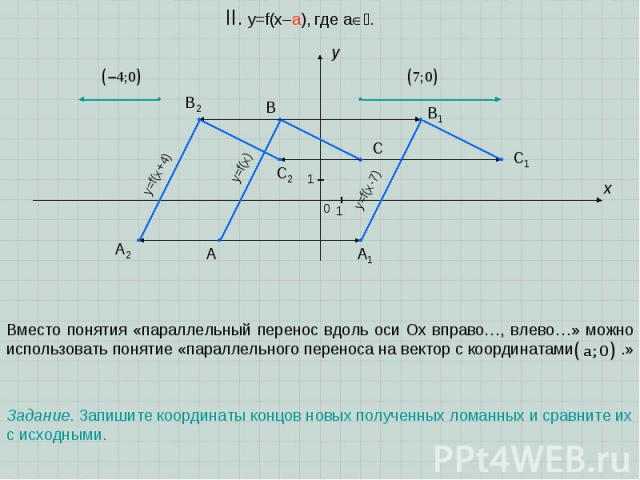
A B C x y 0 1 1 II. y=f(x–a), где a. В новой формуле значения аргумента (абсциссы точек графика) изменяются на число a, по сравнению со «старым» значением аргумента. Это приводит к параллельному переносу графика функции вдоль оси Ox: вправо на a ед.отр., если a>0 или влево на a ед.отр., если a

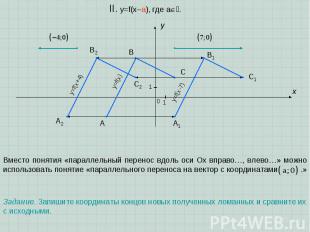
A B C x y 0 1 1 II. y=f(x–a), где a. Вместо понятия «параллельный перенос вдоль оси Oх вправо…, влево…» можно использовать понятие «параллельного переноса на вектор с координатами .» y=f(x) y=f(x-7) A1 B1 C1 A2 B2 C2 y=f(x+4) Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.

A B C x y III. y=–f(x). 0 1 1 A1 B1 C1 В данной формуле значения функции (ординаты точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси Ох. Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными. y=f(x) y=–f(x)

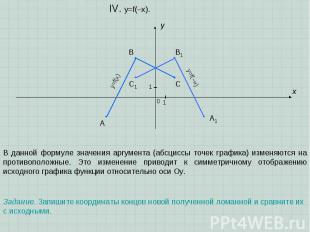
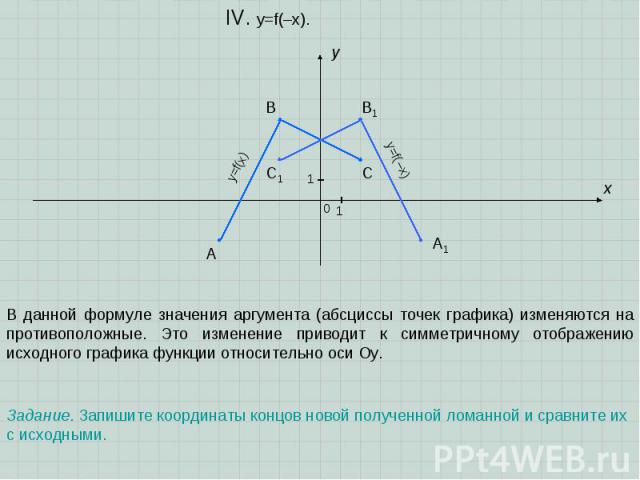
A B C x y 0 1 1 IV. y=f(–x). В данной формуле значения аргумента (абсциссы точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси Оу. A1 B1 C1 Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными. y=f(x) y=f(–x)

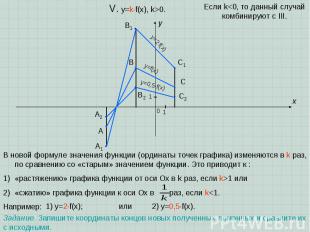
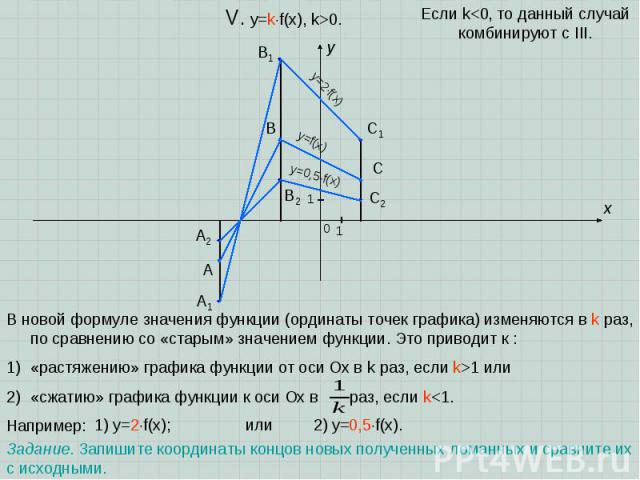
A B C x y 0 1 1 V. y=kf(x), k>0. В новой формуле значения функции (ординаты точек графика) изменяются в k раз, по сравнению со «старым» значением функции. Это приводит к : «растяжению» графика функции от оси Oх в k раз, если k>1 или «сжатию» графика функции к оси Ох в раз, если k

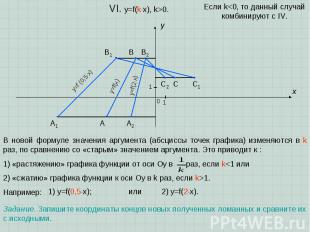
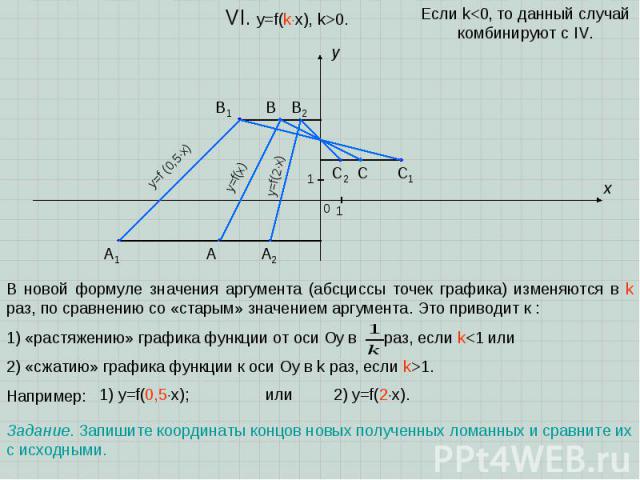
A B C x y 0 1 1 VI. y=f(kx), k>0. В новой формуле значения аргумента (абсциссы точек графика) изменяются в k раз, по сравнению со «старым» значением аргумента. Это приводит к : 1) «растяжению» графика функции от оси Oу в раз, если k1. Например: Если k

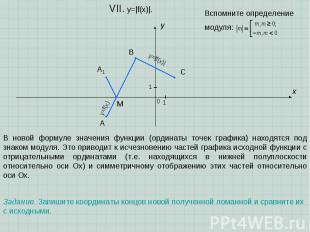
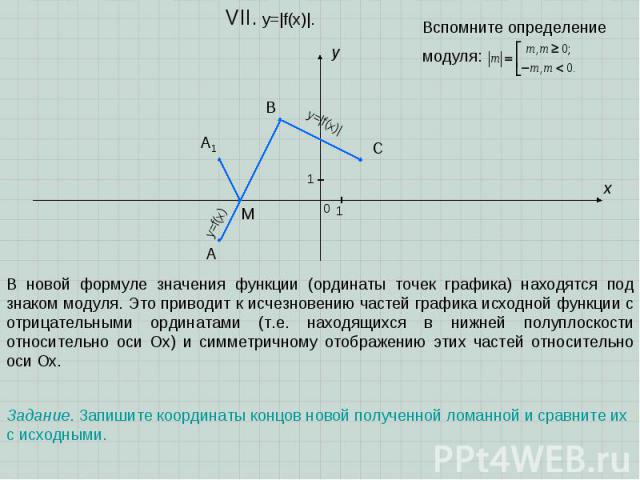
A B C x y 0 1 1 VII. y=|f(x)|. Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными. В новой формуле значения функции (ординаты точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными ординатами (т.е. находящихся в нижней полуплоскости относительно оси Ох) и симметричному отображению этих частей относительно оси Ох. A1 M Вспомните определение модуля: y=f(x) y=|f(x)|

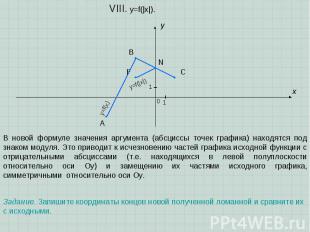
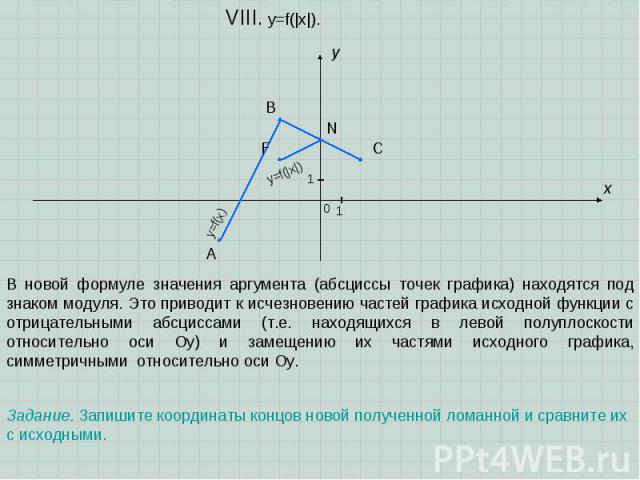
A B C x y 0 1 1 VIII. y=f(|x|). Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными. В новой формуле значения аргумента (абсциссы точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными абсциссами (т.е. находящихся в левой полуплоскости относительно оси Оу) и замещению их частями исходного графика, симметричными относительно оси Оу. N F y=f(x) y=f(|x|)

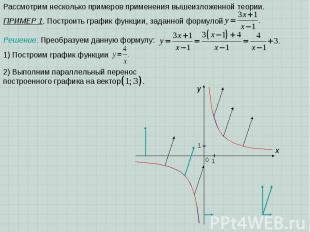
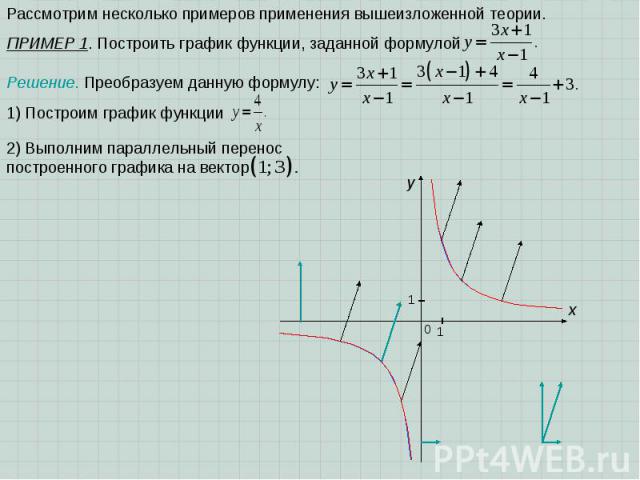
x 0 1 1 y Рассмотрим несколько примеров применения вышеизложенной теории. ПРИМЕР 1. Построить график функции, заданной формулой Решение. Преобразуем данную формулу: 1) Построим график функции 2) Выполним параллельный перенос построенного графика на вектор

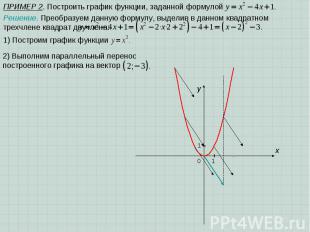
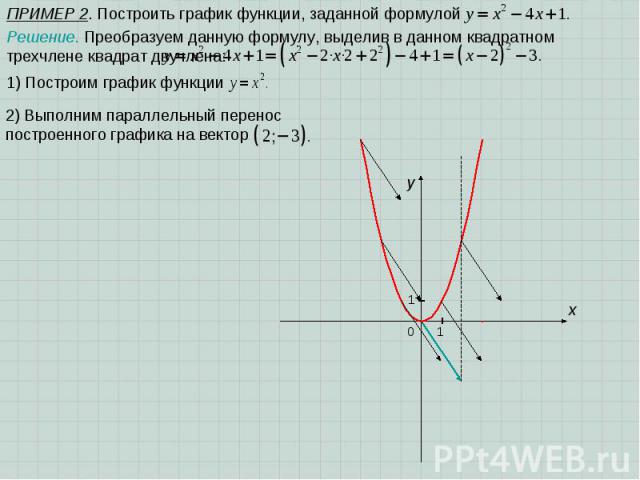
ПРИМЕР 2. Построить график функции, заданной формулой Решение. Преобразуем данную формулу, выделив в данном квадратном трехчлене квадрат двучлена: 1) Построим график функции x 1 y 0 1 2) Выполним параллельный перенос построенного графика на вектор

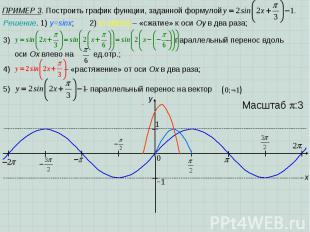
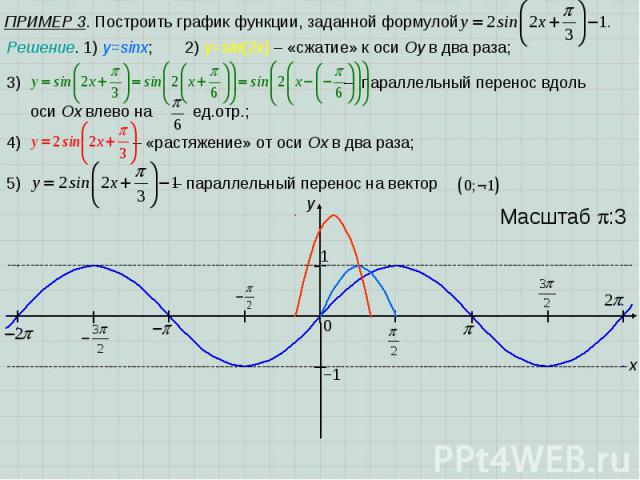
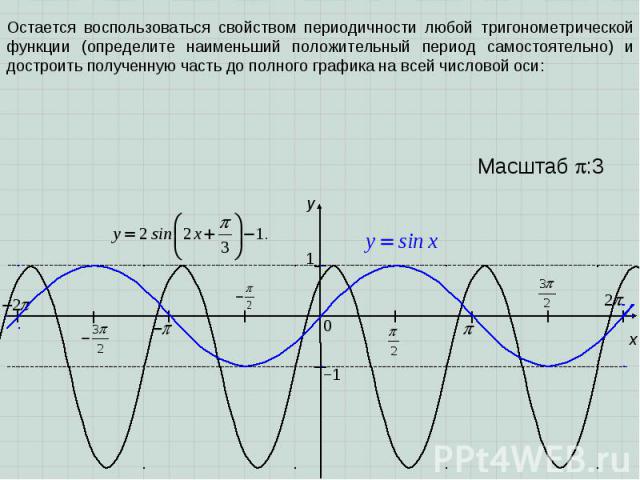
ПРИМЕР 3. Построить график функции, заданной формулой x y 1 0 Масштаб :3 −1 Решение. 1) y=sinx; 2) y=sin(2x) – «сжатие» к оси Оу в два раза; – параллельный перенос вдоль оси Ох влево на ед.отр.; 4) – «растяжение» от оси Ох в два раза; 5) – параллельный перенос на вектор .

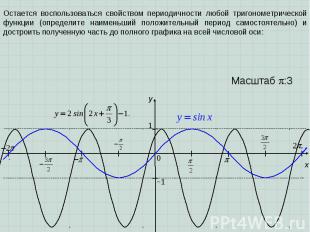
x y 1 0 Масштаб :3 −1 Остается воспользоваться свойством периодичности любой тригонометрической функции (определите наименьший положительный период самостоятельно) и достроить полученную часть до полного графика на всей числовой оси: