Презентация на тему: Геометрические преобразования графиков функций

Геометрические преобразования графиков функций. Алгебра 9 класс Гимназия № 19 г. Минск. Учитель математики В.И. Синявский.

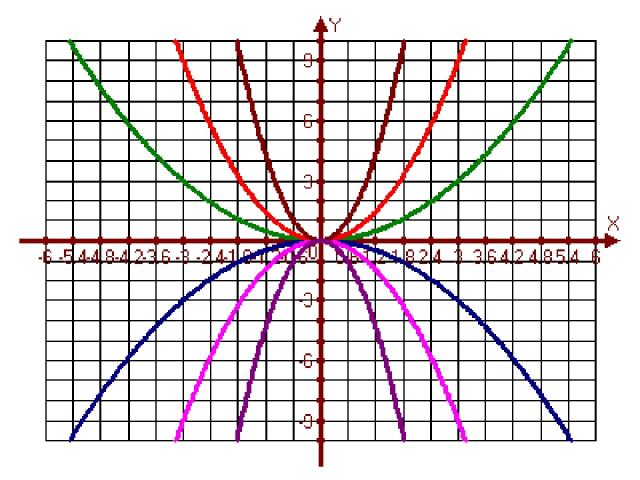
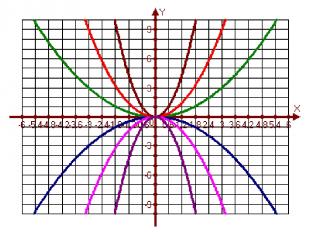
1. Как по графику функции y = f(x) можно построить график функции y = - f(x) ? График функции y = - f(x) получается из графика функции y = f(x) с помощью симметрии относительно оси Ох Приведём примеры графиков

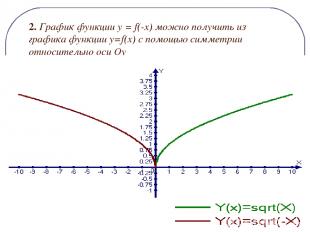
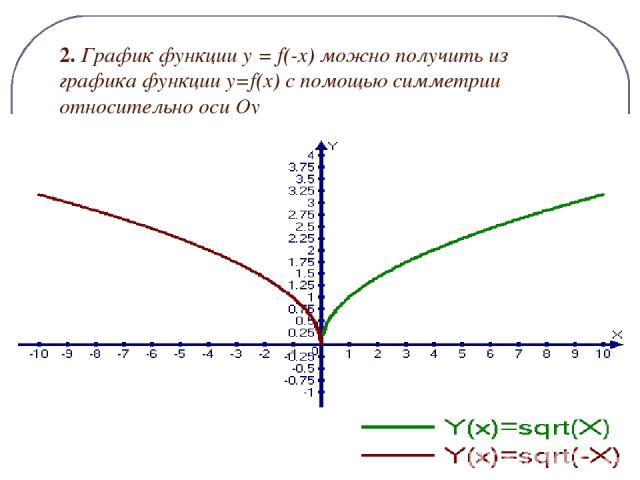
2. График функции y = f(-x) можно получить из графика функции y=f(x) c помощью симметрии относительно оси Оу

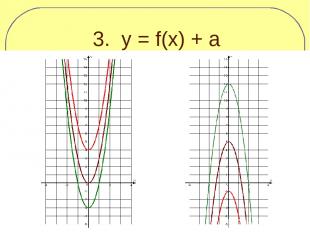
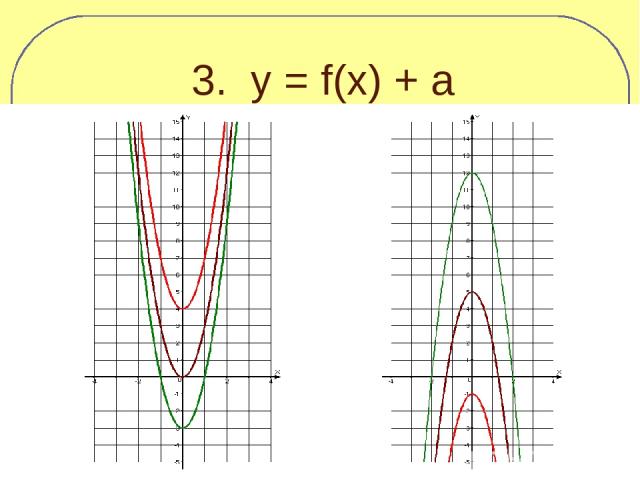
3. y = f(x) + a

y = f(x) + a График функции y = f(x) + a можно получить из графика функции y = f(x) параллельным переносом вдоль оси Оу на расстояние а вверх, если а>0, и на расстояние |a| вниз, если а

4. y = k· f(x), k>0 Пусть точка М принадлежит графику функции y = f(x), а точка М‘ – графику функции y = k· f(x). Обе функции имеют одну и ту же область определения. Рассмотрим следующие случаи:

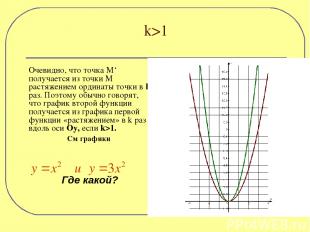
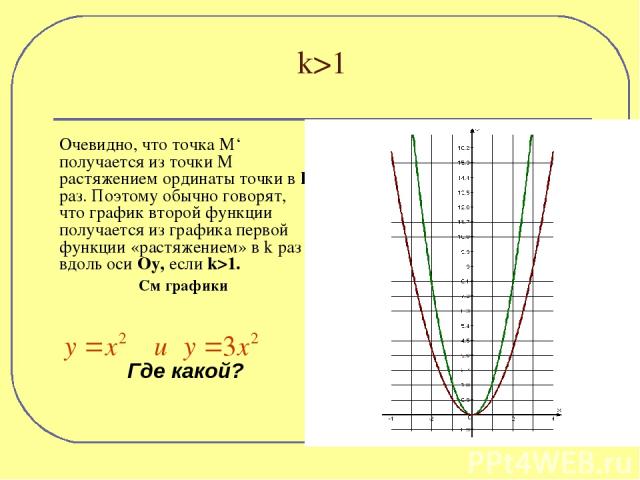
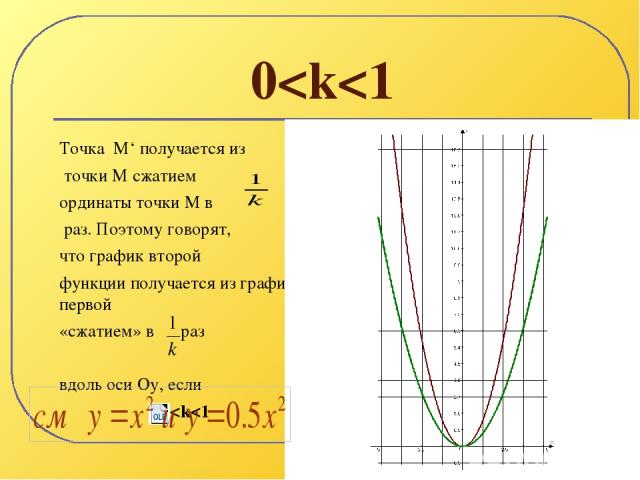
Очевидно, что точка М‘ получается из точки М растяжением ординаты точки в k раз. Поэтому обычно говорят, что график второй функции получается из графика первой функции «растяжением» в k раз вдоль оси Оу, если k>1. См графики Где какой? k>1

2) k=1 При k=1 графики обеих функций, естественно, совпадают. У кого есть сомнения?

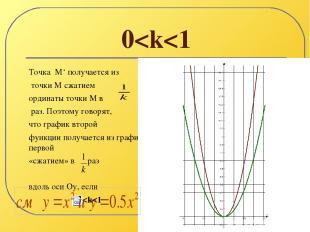
0

5. Как построить график y=f(kx)?

k>1. Точка А‘ получается из точки А сжатием абсциссы точки А в k раз. Поэтому обычно говорят что график второй функции получается из графика первой функции сжатием в k раз вдоль оси Ох, если k>1. k=1. Графики функций совпадают. 0

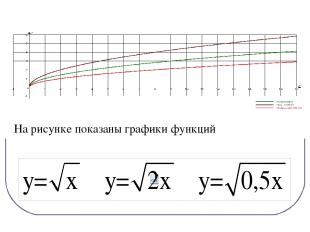
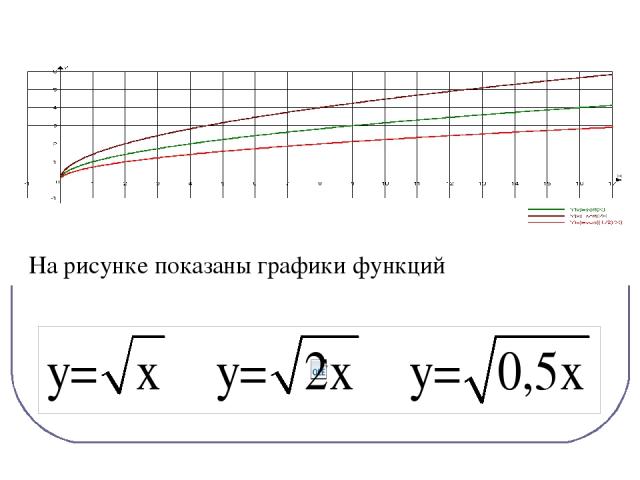
На рисунке показаны графики функций

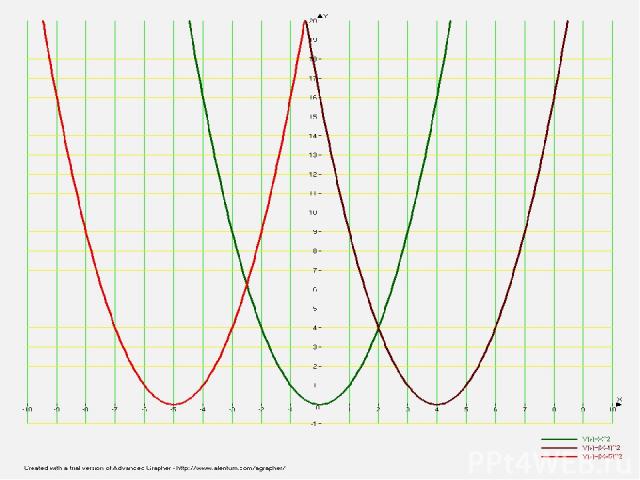
6. y=f(х – а) График функции y=f(x – a) получается из графика функции y=f(x ) параллельным переносом вдоль оси Ох на расстояние a вправо, если a>0, и на расстояние |a| влево, если a

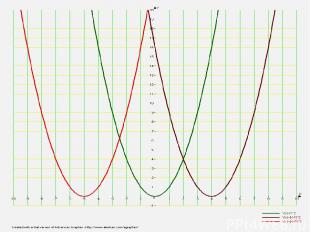
7. y = |f(x)| По определению модуля имеем: Это значит, что график функции y=|f(x)| можно получить следующим образом:

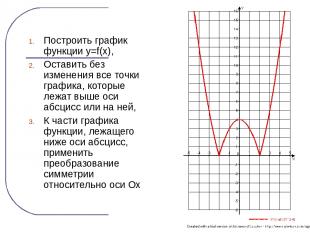
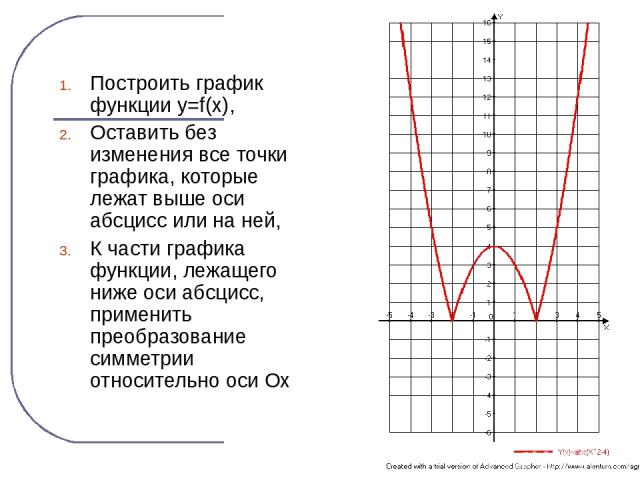
Построить график функции y=f(x), Оставить без изменения все точки графика, которые лежат выше оси абсцисс или на ней, К части графика функции, лежащего ниже оси абсцисс, применить преобразование симметрии относительно оси Ох

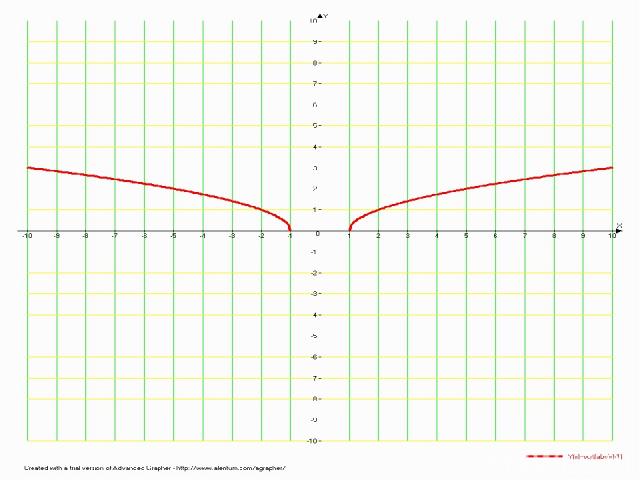
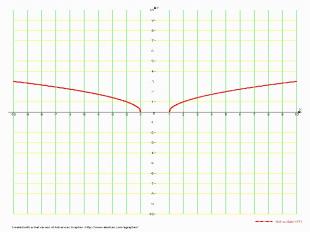
8. y=f(|x|) Функция y=f(|x|) чётная и поэтому её график симметричен относительно оси Оу. Значит, для построения графика заданной функции нужно построить график функции y=f(x) при х ≥ 0, а при х

КОНЕЦ