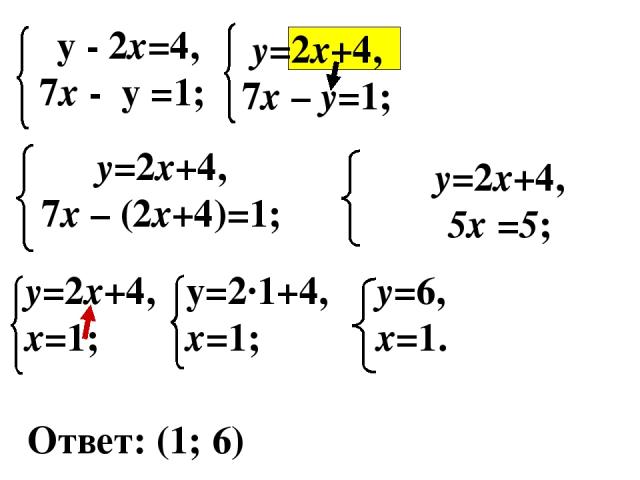Презентация на тему: Системы линейных уравнений

Опр.: Уравнение вида называется линейным уравнением с двумя переменными

{ Опр.: Запись вида называют системой линейных уравнений.

Способы решения систем линейных уравнений. 1. Графический а) В КАЖДОМ уравнении выразить y через x, то есть привести к виду y = kx + b б) На СК построить графики данных функций

в) Находим КООРДИНАТЫ точки ПЕРЕСЕЧЕНИЯ графиков функций (показать на СК пунктиром) Пример: { { { {

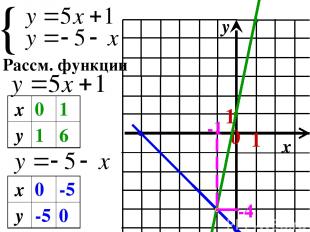
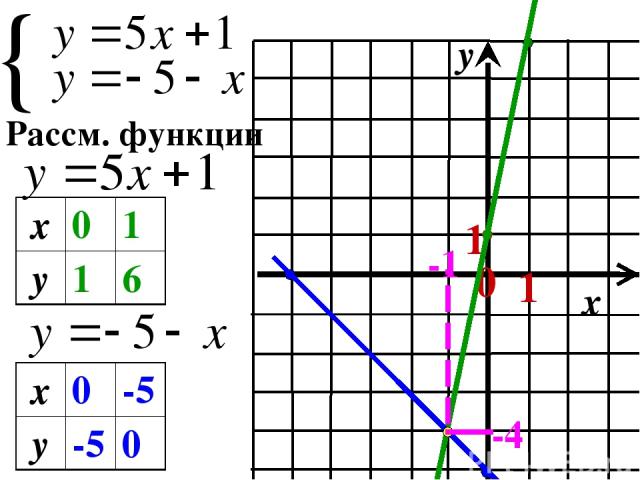
{ Рассм. функции 0 1 1 -1 -4 x 0 1 y 1 6 x 0 -5 y -5 0

Ответ: (-1; -4) 2. Аналитический (с помощью алгебраических преобразований) а) Метод подстановки . Алгоритм: 1)Из какого-либо уравнения ВЫРАЗИТЬ ОДНУ переменную ЧЕРЕЗ другую. 2) Подставить ПОЛУЧЕННОЕ выражение для переменной в другое уравнение и решить его

3)Сделать ПОДСТАНОВКУ найденного значения переменной и вычислить значение второй переменной 4) Записать ответ. Пример:

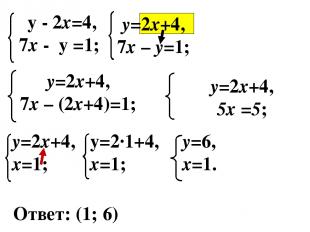
Ответ: (1; 6)

б) Метод сложения. Алгоритм: 1)Преобразовать уравнения ТАК, чтобы соответствующие коэффициенты были противоположными числами 2) Соответственно СЛОЖИТЬ ЧАСТИ уравнений 3) К полученному уравнению ДОБАВИТЬ одно из уравнений системы, которое попроще

4) Решив уравнение с одной переменной, подставляем найденное значение во второе уравнение для определения второй переменной 5) Записать ответ. Пример:

|·(-3) Ответ: (3; - 10)