Презентация на тему: Системы линейных уравнений

Системы линейных уравнений Лекция 3

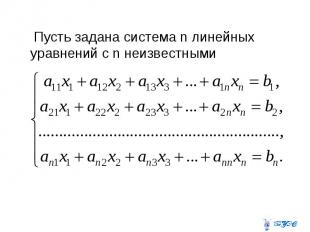
Пусть задана система n линейных уравнений с n неизвестными

Совокупность значений неизвестных где i =1, 2, …, n, при подстановке которых уравнения системы обращаются в равенства, назовем решением системы.

Система, имеющая хоть одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной. Система, имеющая единственное решение, называется определенной. Система, имеющая более одного решения, называется неопределенной.

Правило Крамера решения систем линейных уравнений

Рассмотрим систему линейных уравнений Система трех уравнений может быть решена по правилу Крамера,

Составим определитель из коэффициентов при неизвестных Назовем его определителем системы. Если Δ≠0, то система совместна

Далее составим три вспомогательных определителя: , ,

Решение системы (10) находим по формулам: , , которые называют формулами Крамера

Замечание. Правило Крамера при n>3 не имеет практического применения из-за громоздкости вычислений.

Пример Решить систему уравнений

Решение систем линейных уравнений средствами матричного исчисления

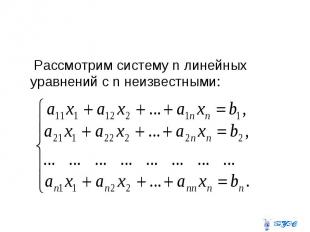
Рассмотрим систему n линейных уравнений с n неизвестными:

Составим из коэффициентов при неизвестных матрицу и назовем ее матрицей системы.

Матрицу называют матрицей-столбцом из свободных членов, а матрицу - матрицей-столбцом из неизвестных.

Запишем систему уравнений в виде матричного уравнения . Умножая обе части этого уравнения слева на , получим: .

Таким образом, если матрица А системы невырожденная, т.е. существует , то решение системы линейных уравнений можно найти по формуле .

Замечание Метод матричного исчисления обычно применяют для решения систем трех уравнений с тремя неизвестными. Решать этим методом системы с большим числом уравнений и неизвестных неудобно, так как он приводит к громоздким выкладкам.

Пример Средствами матричного исчисления решить систему линейных уравнений

Ранг матрицы Рангом матрицы называется наивысший из порядков отличных от нуля миноров матрицы. Ранг матрицы A обозначается: или .

Элементарные преобразования матрицы Для вычисления ранга матрицы ее сначала приводят к более простому виду с помощью так называемых элементарных преобразований, к которым относятся:

1.Умножение всех элементов строк на одно и то же число не равное 0. 2. Перестановка строк местами. 3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и тоже число.

4.Отбрасывание одной из двух одинаковых строк. 5.Отбрасывание нулевой строки

Теорема: Элементарные преобразования не меняют ранг матрицы. Матрицы, полученные с помощью элементарных преобразований, называют эквивалентными (~).

Пример С помощью элементарных преобразований вычислить ранг матрицы

Понятие о линейной зависимости Рассмотрим матрицу Обозначим ее строки Очевидно . Это равенство понимается в смысле поэлементного сложения.

Строки матрицы А линейно зависимы, если можно подобрать такие не равные нулю одновременно числа , что . Если таких чисел подобрать нельзя, то строки матрицы линейно независимы.

Если одна из строк матрицы линейно выражается через другие строки, то строки этой матрицы между собой линейно зависимы.

Пример Строки такой матрицы линейно независимы (лнз), так как их невозможно выразить одну через другую:

Теорема о ранге матрицы Ранг матрицы равен максимальному числу линейно – независимых строк матрицы.

Теорема. Если ранг матрицы равен r, то в этой матрице можно найти r линейно независимых строк ( столбцов), через которые линейно выражаются остальные строки ( столбцы) матрицы.

Теорема. Для того чтобы определитель был равен нулю, необходимо и достаточно, чтобы его строки ( столбцы) были линейно зависимы.