Презентация на тему: Геометрические приложения двойного интеграла

Геометрические приложения двойного интеграла Лекция 8

Примеры Пример 1. Вычислить где D – трапеция с вершинами А(1;1), В(5;1), С(10;2), D(2;2).

Решение Имеем =

Примеры Пример 2. Вычислить где D – треугольник с вершинами О(0;0), А(1;1) и В(0;1).

Решение Получаем = =

Примеры Пример 3. Изменить порядок интегрирования в двукратном интеграле

Двойной интеграл в полярных координатах Элемент площади в полярных координатах вычисляют так: =

Замена переменных = Выражение = называется двумерным элементом площади в полярных координатах.

Замена переменных Для того чтобы в двойном интеграле перейти к полярным координатам, достаточно координаты x и y положить равными и соответственно, а вместо элемента площади подставить его выражение в полярных координатах.

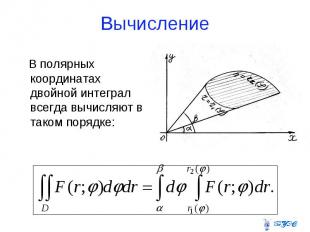
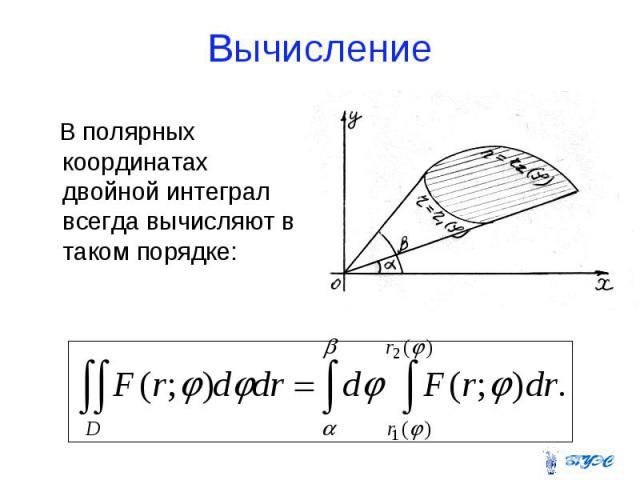
Вычисление В полярных координатах двойной интеграл всегда вычисляют в таком порядке:

Площадь плоской фигуры Площадь плоской фигуры в декартовых координатах вычисляют по формуле:

Площадь в полярных координатах Если фигура ограничена кривыми, заданными в полярных координатах, или ее уравнение содержит двучлен

Вычислить площадь Фигура ограничена кривыми х+у=2 и

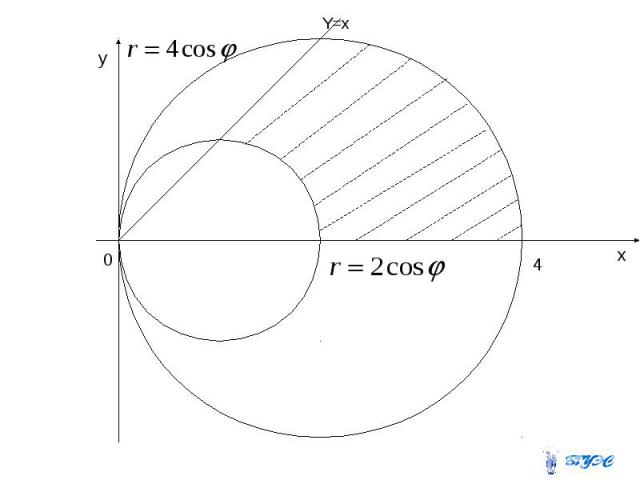
Вычислить площадь фигуры, ограниченной линиями Перейдем к полярным координатам и изобразим фигуру.

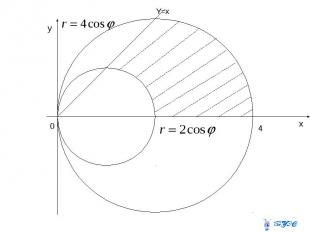
Решение Площадь области D вычислим в полярных координатах

Вычисление объемов тел с помощью двойного интеграла Пусть тело ограничено с боков цилиндрической поверхностью с образующими, параллельными оси Оz, а снизу и сверху соответственно поверхностями

Формула для вычисления объема Тогда объем тела равен разности объемов цилиндроидов и вычисляется по формуле:

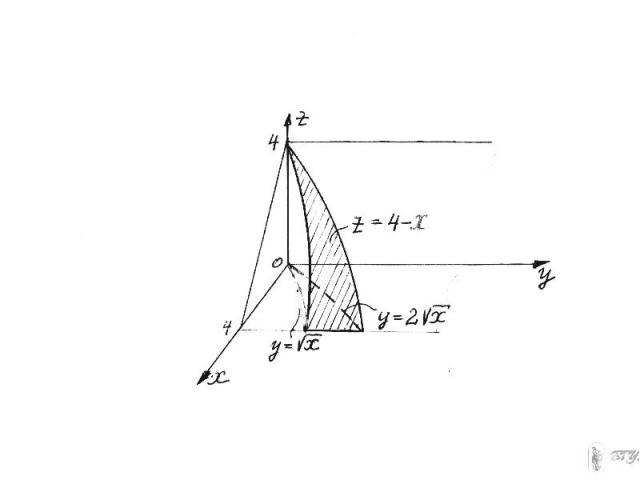
Вычислить объем тела, ограниченного поверхностями x+z=4, z=0, , .

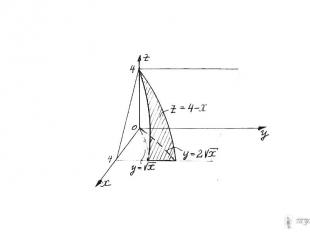
Вычислить объем тела Запишем объем в виде двойного интеграла:

Найти объем тела, ограниченного цилиндром радиуса 1, плоскостью Оxy и конусом Запишем объем Вычислим его в полярных координатах