Презентация на тему: Количество решений систем линейных уравнений с двумя переменными

Математическоеисследование по теме: "Количество решений системлинейных уравнений с двумя переменными" Выполнили:Лисуненко М.,Кашликов Д.,учащиеся 7 В класса,Клименко Е.,учащаяся 11 А классаМОУСОШ №33

Цель: Научиться находить множество решений двух или нескольких линейных уравнений с двумя переменными. Научиться составлять такие системы по заданным условиям.

Говорят, что древнегреческие математики при доказательстве теорем часто ограничивались тем, что рисовали чертёж, сопровождая его всего лишь одним словом: «Смотри!» . Иногда так можно доказать довольно сложные формулы.

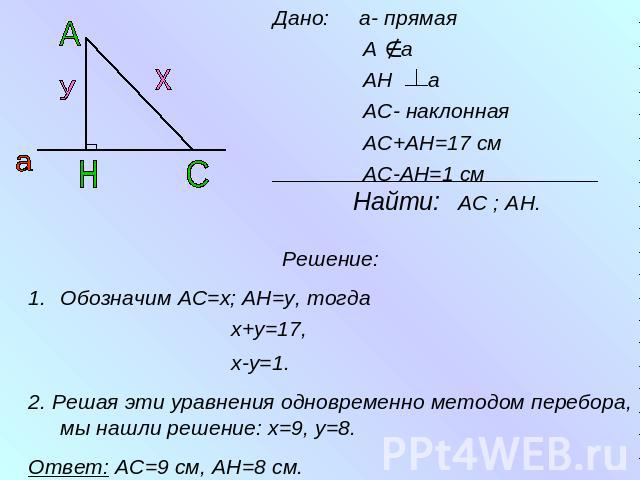
Геометрия 7 класс. №271 Из точки к прямой проведены перпендикуляр и наклонная, сумма длин которых равна 17 см, а разность длин равна 1 см. Найдите расстояние от точки до прямой.

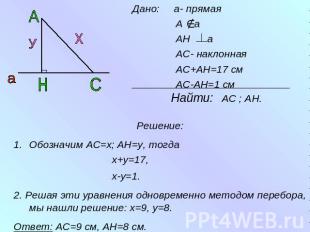
Дано: а- прямая А а АН а АС- наклонная АС+АН=17 см АС-АН=1 см

ах+ву+с=0, а=0, в=0 –линейное уравнение с двумя переменными х и у. Теорема. Графиком любого линейного уравненияах+ву+с=0 является прямая.

Взаимное расположение прямых на плоскости:

Следовательно, системы двух линейных уравнений с двумя переменными могут иметь:Единственное решение.2. Не иметь решений.3. Иметь бесконечно много решений.

Если , то система имеет единственное решение. 2. Если , то система несовместна ( решений нет) 3. Если , система неопределенна (имеет бесконечно много решений)

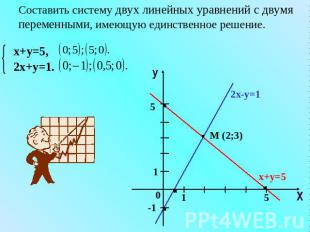
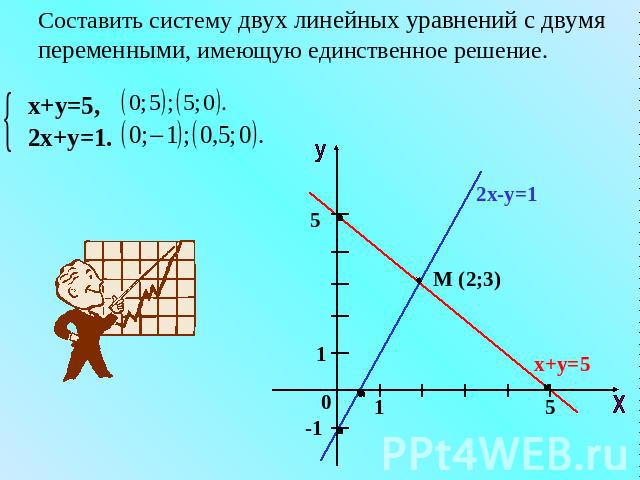
Составить систему двух линейных уравнений с двумя переменными, имеющую единственное решение.

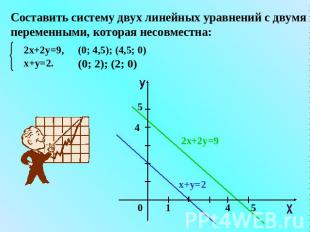
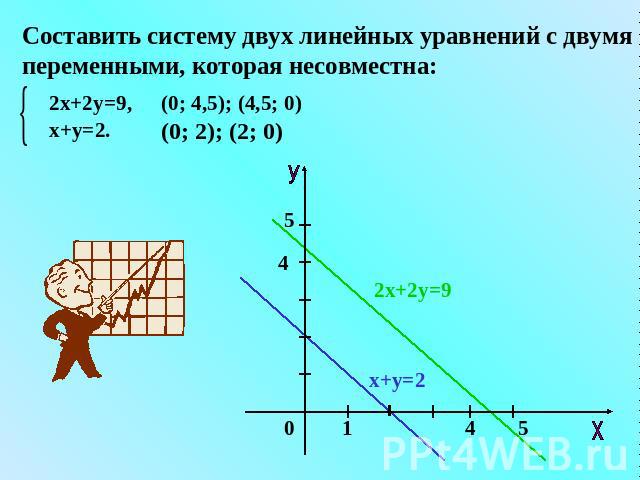
Составить систему двух линейных уравнений с двумя переменными, которая несовместна: 2х+2у=9, х+у=2. (0; 4,5); (4,5; 0) (0; 2); (2; 0)

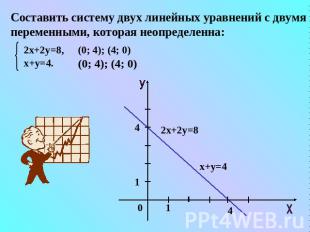
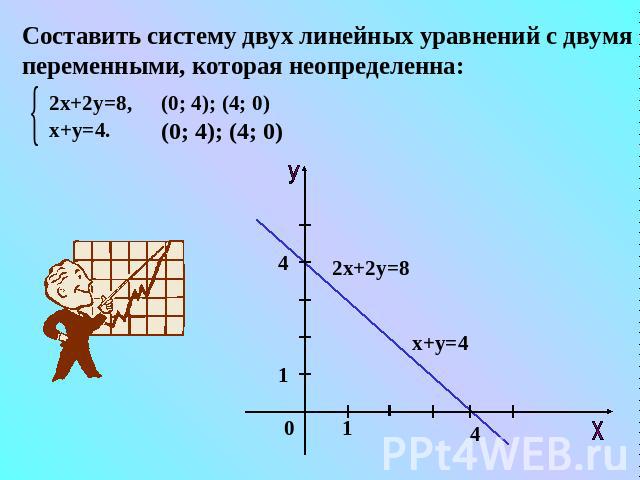
Составить систему двух линейных уравнений с двумя переменными, которая неопределенна: 2х+2у=8, х+у=4. (0; 4); (4; 0) (0; 4); (4; 0)

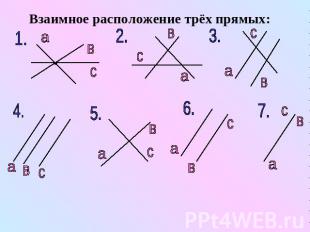
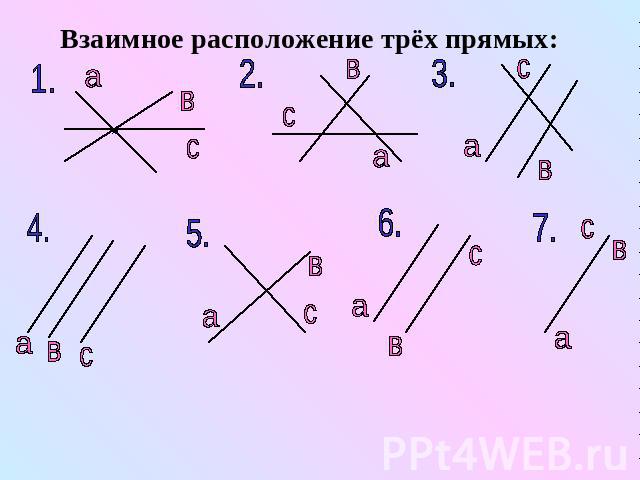
Взаимное расположение трёх прямых:

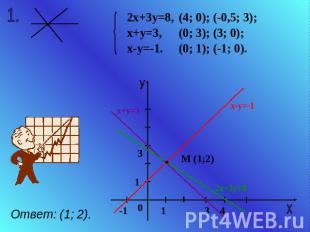
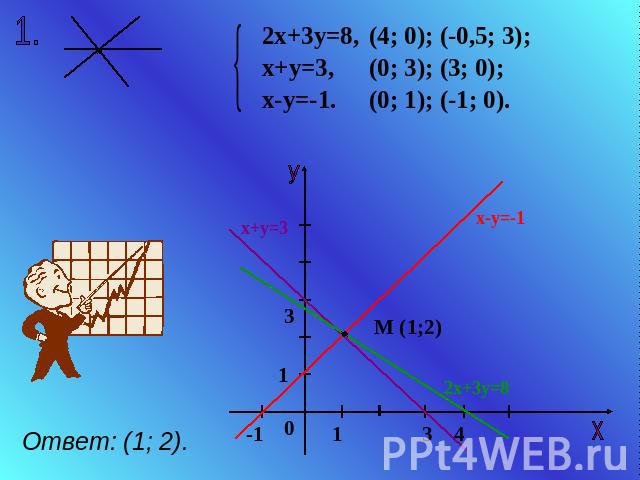
2х+3у=8, х+у=3, х-у=-1. (4; 0); (-0,5; 3); (0; 3); (3; 0); (0; 1); (-1; 0). Ответ: (1; 2).

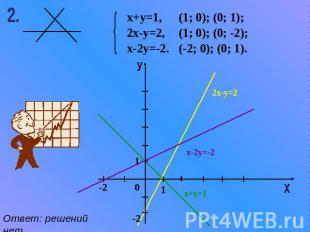
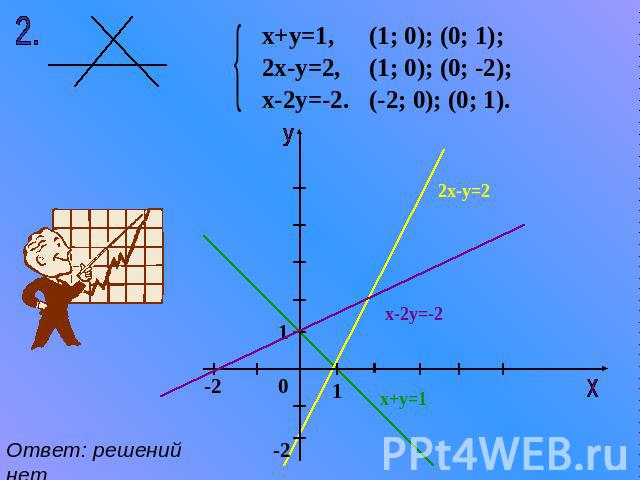
(1; 0); (0; 1); х+у=1, 2х-у=2, х-2у=-2. (1; 0); (0; -2); (-2; 0); (0; 1). Ответ: решений нет

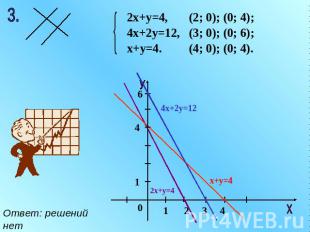
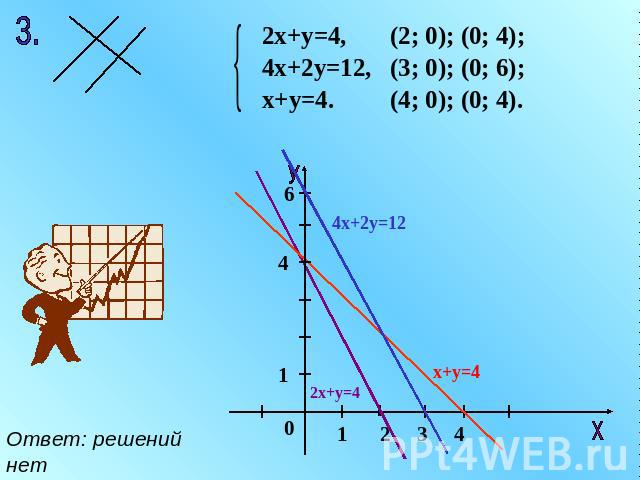
Ответ: решений нет 2х+у=4, 4х+2у=12, х+у=4. (2; 0); (0; 4); (3; 0); (0; 6); (4; 0); (0; 4).

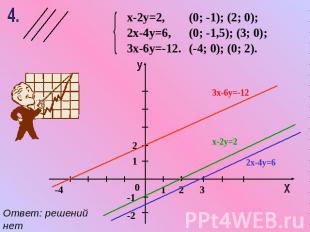
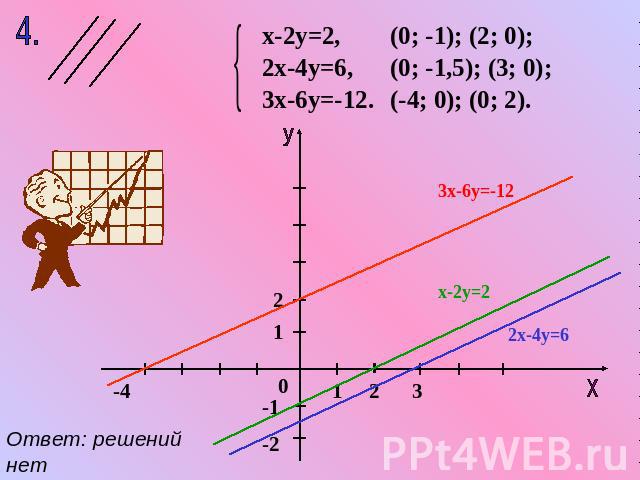
х-2у=2, 2х-4у=6, 3х-6у=-12. (0; -1); (2; 0); (0; -1,5); (3; 0); (-4; 0); (0; 2). Ответ: решений нет

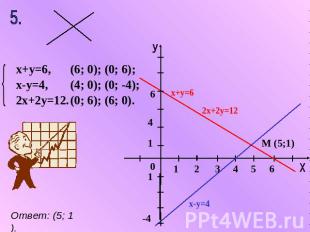
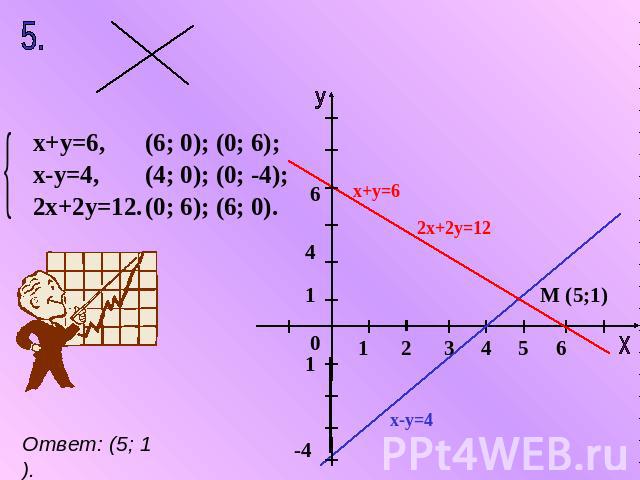
х+у=6, х-у=4, 2х+2у=12. (6; 0); (0; 6); (4; 0); (0; -4); (0; 6); (6; 0). Ответ: (5; 1).

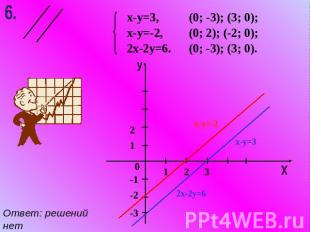
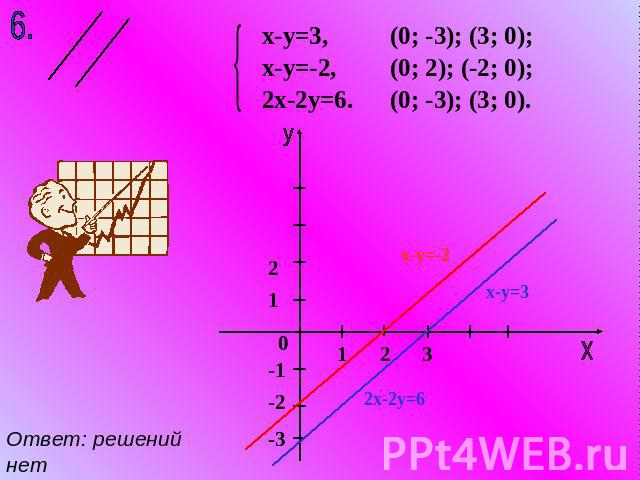
х-у=3, х-у=-2, 2х-2у=6. (0; -3); (3; 0); (0; 2); (-2; 0); (0; -3); (3; 0). Ответ: решений нет

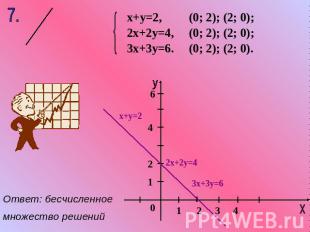
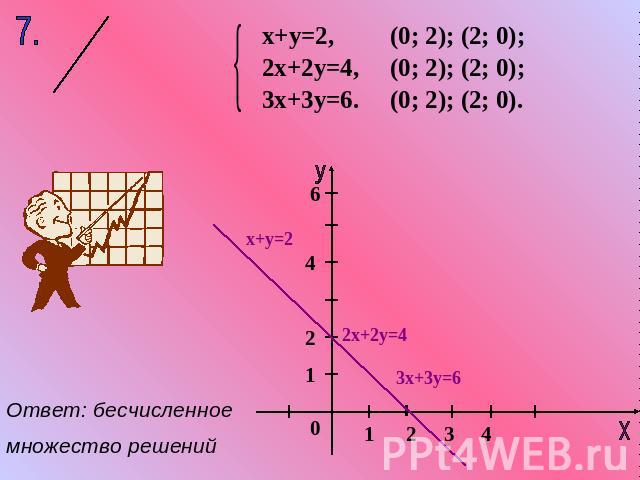
х+у=2, 2х+2у=4, 3х+3у=6. (0; 2); (2; 0); (0; 2); (2; 0); (0; 2); (2; 0). Ответ: бесчисленноемножество решений

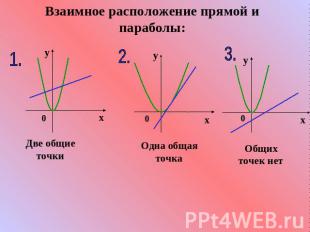
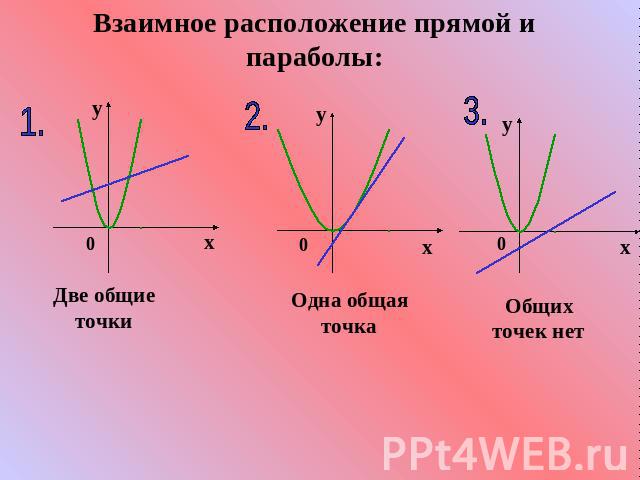
Взаимное расположение прямой и параболы: Две общие точки Одна общая точка Общих точек нет

Следовательно, система вида: может иметь:Два решения.2. Одно решение.3. Не иметь решений.

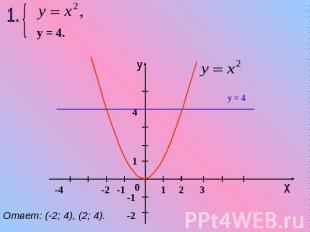
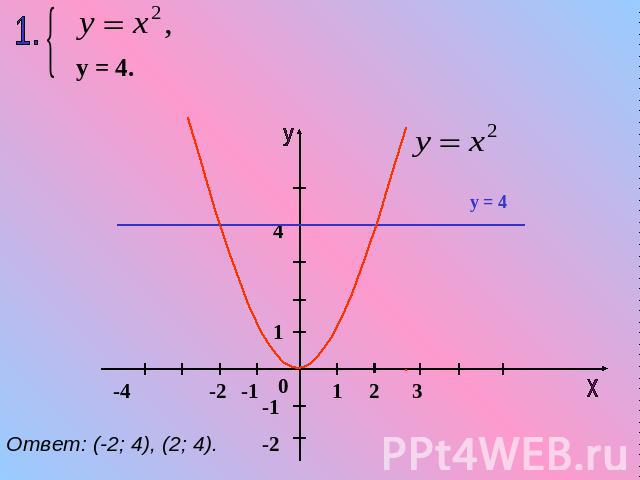
Ответ: (-2; 4), (2; 4).

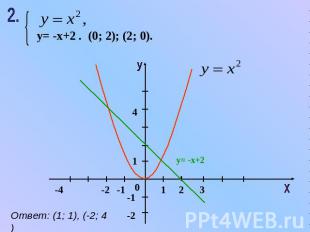
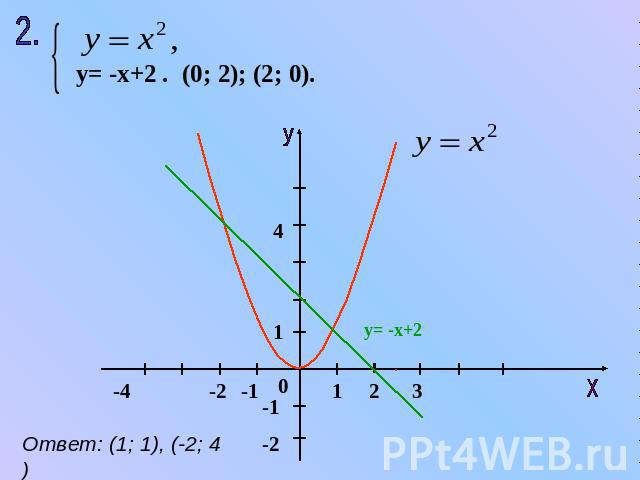
y= -x+2 . (0; 2); (2; 0). Ответ: (1; 1), (-2; 4)

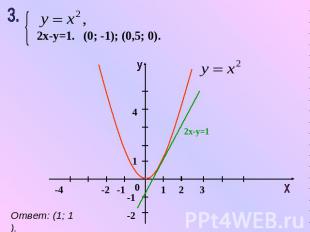
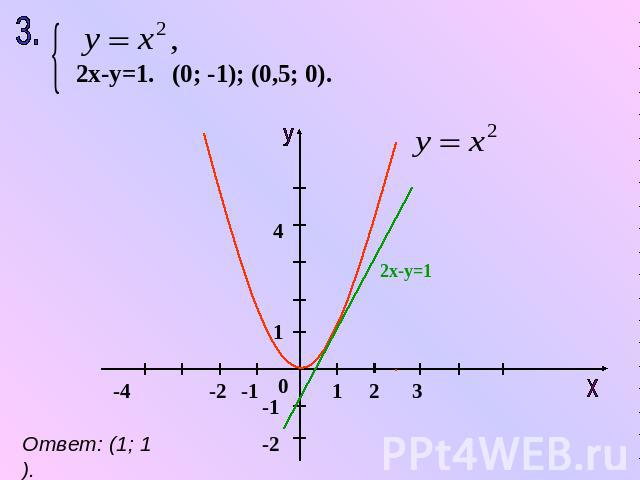
2х-у=1. (0; -1); (0,5; 0). Ответ: (1; 1).

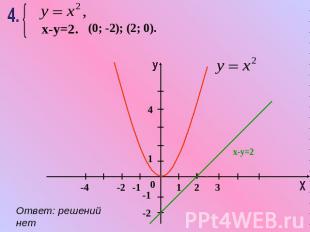
х-у=2. (0; -2); (2; 0).Ответ: решений нет

Спасибо за внимание!