Презентация на тему: История развития понятия функции

Выполнила ученица 10 классаВыщепан Анна.Руководитель: Рожко Ирина Александровна История развития понятия функции

Объект исследования:Функция.Предмет исследования:История развития понятия функции.Гипотеза:Предположим что функция имеет разные определения.Методы исследований:-работа с литературой;-поиск информации во всемирной сети ИнтернетЦель работы:-изучения развития понятия функции с древнейших времен до настоящего времениЗадачи:Рассмотреть свойства элементарных функций.

История развития понятия функции. Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.Высокого уровня математические знания достигли в Древнем Вавилоне. Для облегчения вычислений вавилоняне составили таблицу обратных значений чисел квадратов и кубов и даже таблицы для сумм квадратов и кубов числа.Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет (1540-1603) и Рене Декарт (1596-1650); они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание.

Кроме того, у Декарта и Пьера Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы В 1671 году Ньютон (1643-1727) под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в «флюентой»).

В «Геометрии» Декарта и работах Ферма, Ньютона иЛейбница (1646-1716) понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость – функция от времени (t) и т.п.

Само слово «функция» (от латинского functio - совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. в письме к Гюйгенсу (1629-1695) (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати ввел с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа». В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667-1748) который в 1718 году определил функцию следующимобразом: «функцией переменной величины называют количество, образованное каким угодно способ из этой переменной величины и постоянных».

Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер. «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего 18 века Даламбер Лагранж (1736-1813), Фурье (1768-1830) и другие видные математики

Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье. Из трудов Фурье следовало, что любая кривая независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения и что имеются также прерывные кривые, изображаемые аналитическим выражением В своем «Курсе алгебраического анализа», опубликованном в 1721г., французский математик О. Коши (1789-1857) обосновал выводы Фурье.

Идея соответствия . Н.И. Лобачевский (1792-1856) Еще до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским математиком Б. Больцано (1781-1848)

Таким образом, современное определение функции, свободное от упоминании об аналитическом задании, обычно приписываемое немецкому математику П.Л. Дирихле (1805-1859)

Дальнейшее развитие понятия функции. Необходимость дальнейшего расширения понятия функции стала особенно острой после выхода в свет в 1930 году книги «Основы квантовой механики» Поля Дирака (1902-1984)

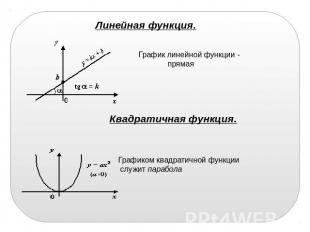
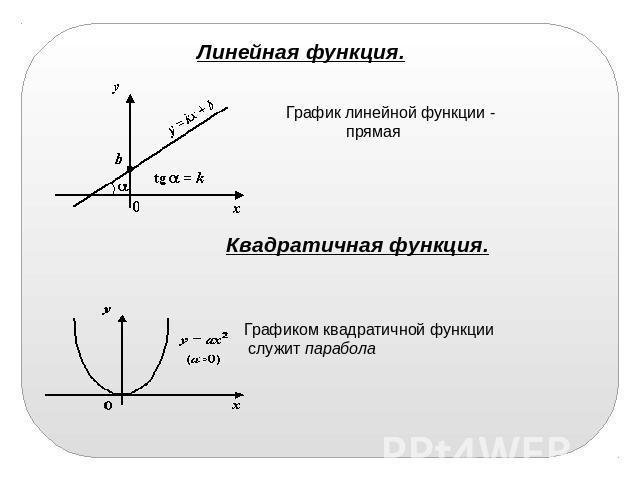
Линейная функция. График линейной функции - прямая Квадратичная функция. Графиком квадратичной функции служит парабола

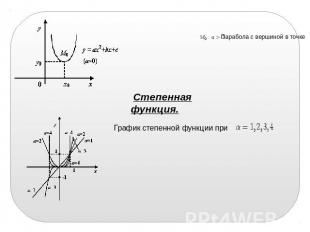
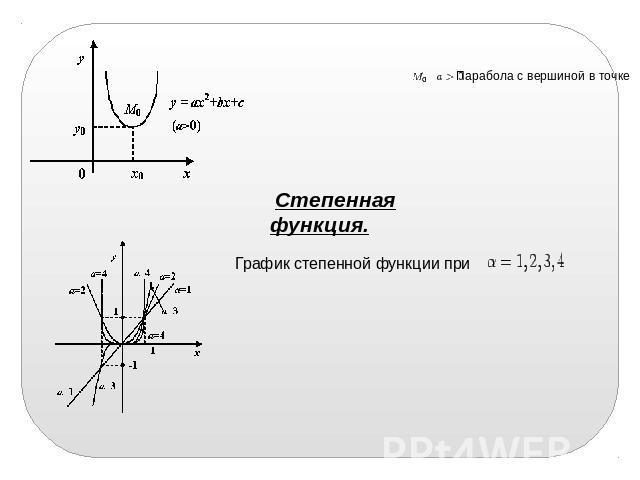
Парабола с вершиной в точке Степенная функция. График степенной функции при

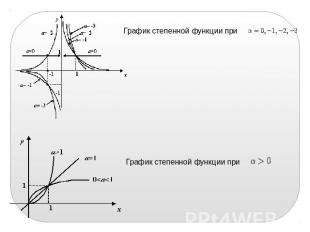
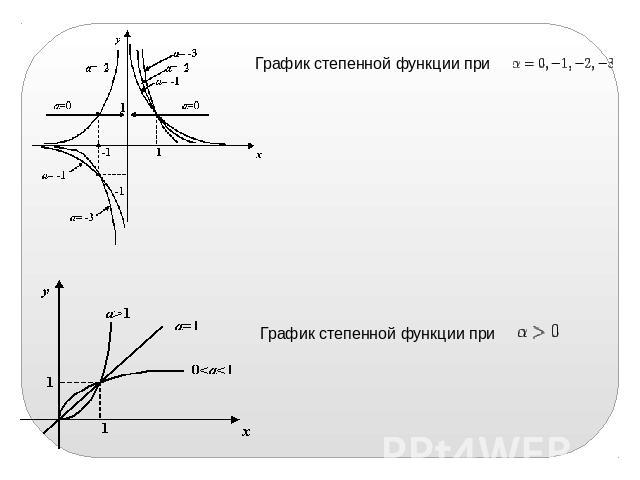
График степенной функции при График степенной функции при

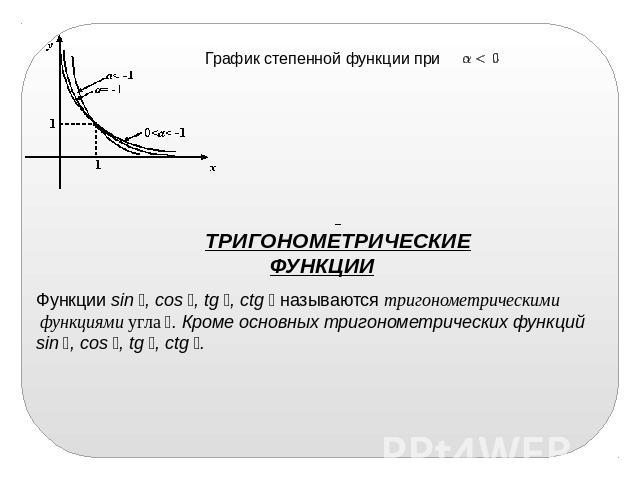
График степенной функции при ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Функции sin , cos , tg , ctg называются тригонометрическими функциями угла . Кроме основных тригонометрических функций sin , cos , tg , ctg .

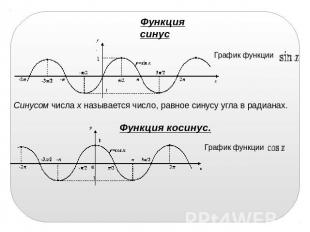
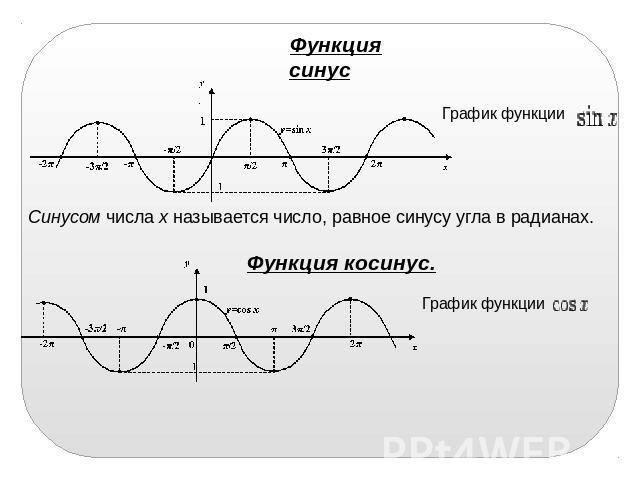
Функция синус График функции Синусом числа х называется число, равное синусу угла в радианах. Функция косинус. График функции

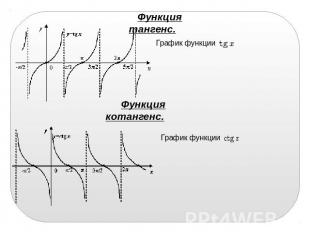
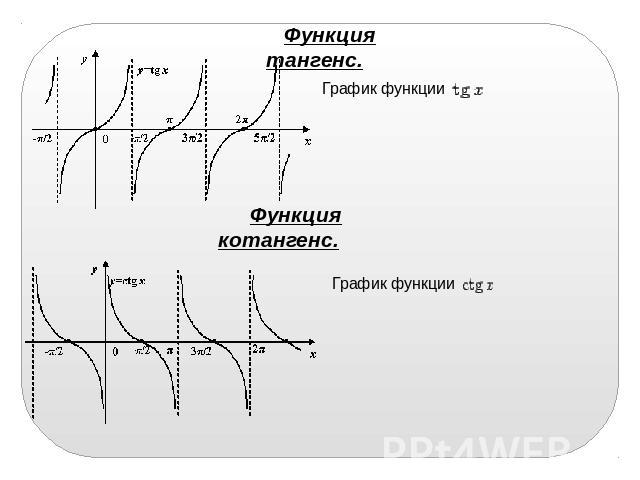
Функция тангенс. График функции Функция котангенс. График функции