Презентация на тему: Исследование зависимости вида y=ax2+bx+c и решение задач на прямолинейное равноускоренное движение

Исследование зависимости видаy=ax2+bx+c и решение задач на прямолинейное равноускоренное движение Искандярова О.Р.

Автор - Искандярова О.Р.Класс – 11 БНаучный руководитель – Тамарлакова Л.И.Консультант по математической части – Белобородова В.А.Тип проекта - интегративный Форма проекта – компьютерная презентация

Если ученику с легкостью даются построения графиков, нахождение производных и решение уравнений с параметрами в математике, то он так же легко сделает это и в физике.

Изучение многих физических процессов часто приводит к решению задач с параметрами. «Параметр» с греч. parametron-отмеривающий. Параметр - это постоянная величина, выраженная буквой, сохраняющая своё постоянное значение в условиях данной задачи.

С параметрами мы встречались, когда вводили понятия: функция прямая пропорциональность: y=kx (x и y-переменные, k-параметр,k ≠ 0);линейная функция: y=kx+b (x и y-переменные, k и b- параметры);линейное уравнение: ax+b=0 ( x-переменная, a и b-параметры);квадратное уравнение: ax2+bx+c=0 (х - переменная, а, b и с-параметры, а ≠ 0).

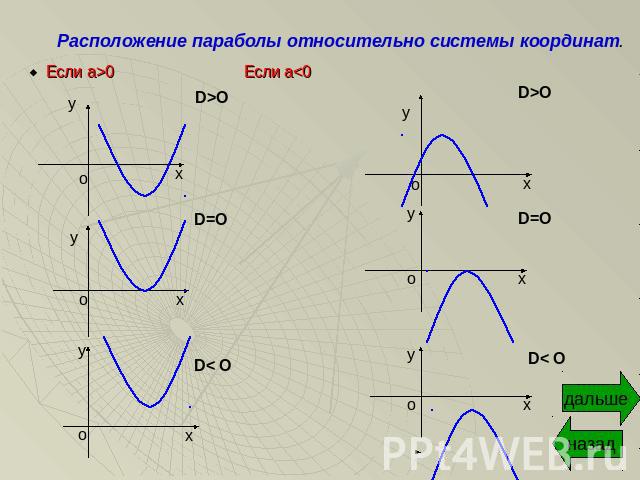
Многочлен ах2+bx+c, где а≠0 и a, b, c- действительные числа, называют квадратным трехчленом.Функция f(x)=ax2+bx+c, (а≠0)- квадратичная, ее график- парабола.Координаты вершины параболы: Х0= - b/2a; y0=f(x0).Если а>0, ветви параболы направлены вверх, если а<0 – вниз.D=b2- 4ac.Если D>0, парабола пересекает ось х в двух точках. Если D=0, парабола касается оси х. Если D<0, парабола не пересекает ось х.

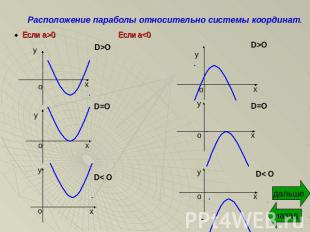
Расположение параболы относительно системы координат.

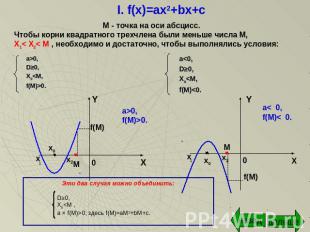
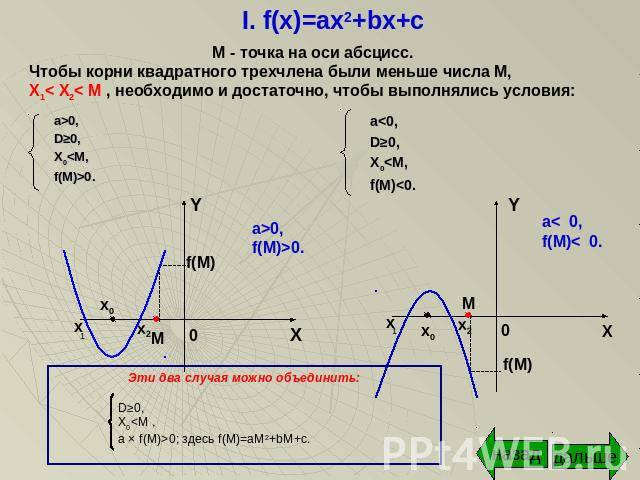
I. f(x)=ax2+bx+c М - точка на оси абсцисс.Чтобы корни квадратного трехчлена были меньше числа М,Х1< X2< М , необходимо и достаточно, чтобы выполнялись условия: Эти два случая можно объединить:D≥0,X0<M ,a × f(M)>0;здесь f(M)=aM2+bM+c.

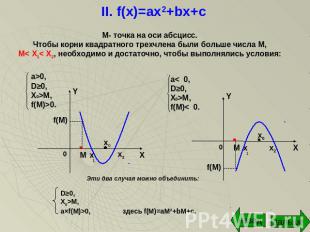
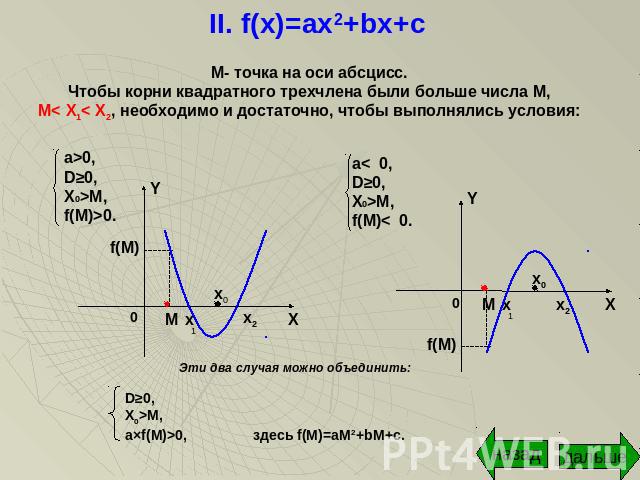
II. f(x)=ax2+bx+c М- точка на оси абсцисс.Чтобы корни квадратного трехчлена были больше числа М,M< X1< X2, необходимо и достаточно, чтобы выполнялись условия: a>0,D≥0,X0>M,f(M)>0. a< 0,D≥0,X0>M,f(M)< 0. Эти два случая можно объединить:D≥0,X0>M,a×f(M)>0, здесь f(M)=aM2+bM+c.

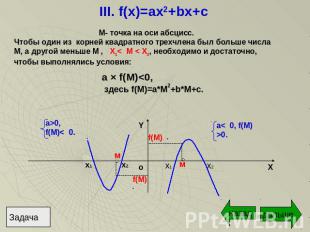
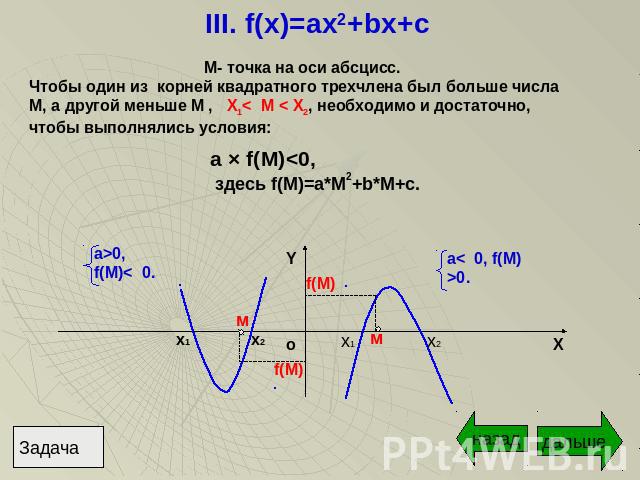
III. f(x)=ax2+bx+c М- точка на оси абсцисс.Чтобы один из корней квадратного трехчлена был больше числа М, а другой меньше M , X1< М < X2, необходимо и достаточно, чтобы выполнялись условия: a × f(M)<0, здесь f(M)=a*M2+b*M+c. a>0,f(M)< 0. a< 0, f(M)>0.

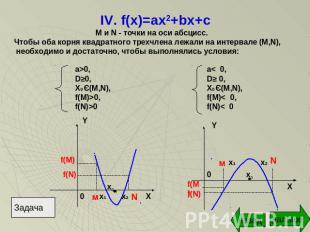
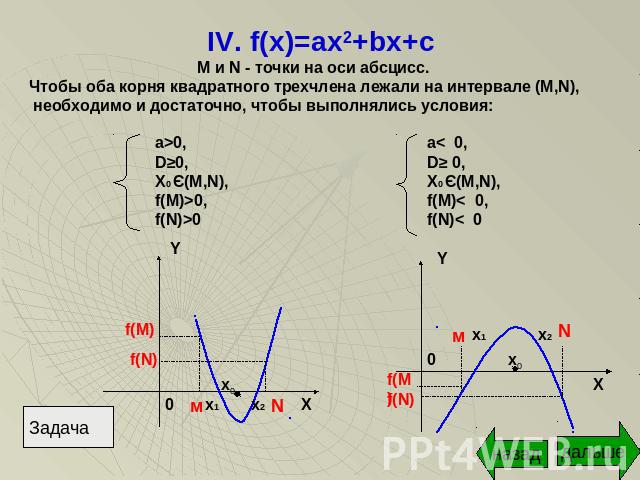
IV. f(x)=ax2+bx+c М и N - точки на оси абсцисс.Чтобы оба корня квадратного трехчлена лежали на интервале (М,N), необходимо и достаточно, чтобы выполнялись условия: a>0,D≥0,X0 Є(M,N),f(M)>0,f(N)>0 a< 0,D≥ 0,X0 Є(M,N),f(M)< 0,f(N)< 0

V. f(x)=ax2+bx+c М и N - точки на оси абсцисс.Чтобы отрезок [М,N] целиком лежал на интервале (x1;х2), необходимо, чтобы выполнялись условия: a*f(M)<0,a*f(N)<0. a>0,f(M)< 0,f(N)< 0. a< 0,f(M)>0,f(N)>0.

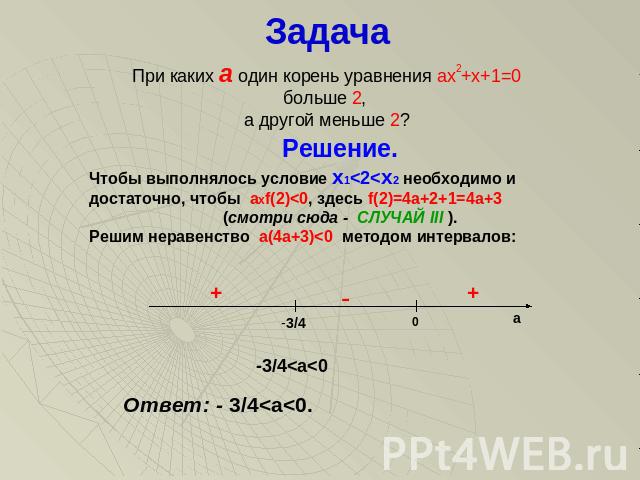
Задача При каких а один корень уравнения ах2+х+1=0 больше 2, а другой меньше 2? Решение.Чтобы выполнялось условие х1<2<х2 необходимо и достаточно, чтобы ахf(2)<0, здесь f(2)=4a+2+1=4a+3 (смотри сюда - СЛУЧАЙ III ).Решим неравенство a(4a+3)<0 методом интервалов: Ответ: - 3/4<a<0.

Задача При каких а оба корня уравнения х2-ах+2=0 лежат на интервале (0;3)? Решение Коэффициент при х2 положителен(a>0). Чтобы х1 и х2 принадлежали интервалу (0;3) необходимо, чтобы выполнялось условие D≥0,X0 Є(M,N),f(M)>0,f(N)>0. здесь D=a2-8, х0=а/2 и f(3)=9-3a+2 (смотри сюда – СЛУЧАЙ IV).Решим получившуюся систему а2-8 ≥ 0,а/2 Є (0;3),9-3а+2 > 0 |а|≥√8,а Є (0;6),а < 11/3 а ≥ 2√2,а Є (0;6),а < 11/3. Ответ: 2√2 ≤ a ≤ 11/3

Задача При каких а один корень уравнения ах2+х+1=0 меньше 0, а второй корень больше 3? РешениеКоэффициент при х2 положителен (a>0). Чтобы х1 был меньше 0, а х2 больше 3, необходимо, чтобы выполнялось условие a*f(0)<0,a*f(3)<0. a*1<0,a*(9a+4)<0 a*1<0,a*(9a+4)<0 a<0,9a2+4a<0 a<0,-4/9<a<0 -4/9<a<0. Ответ: -4/9<a<0.

Прямолинейное равномерное движение

1) x1=-270+12t –движение грузового автомобиляx2=-1.5t – движение пешеходаВопрос: с какими скоростями и в каком направлении они двигались? Когда и где они встретились?

ДаноРешение

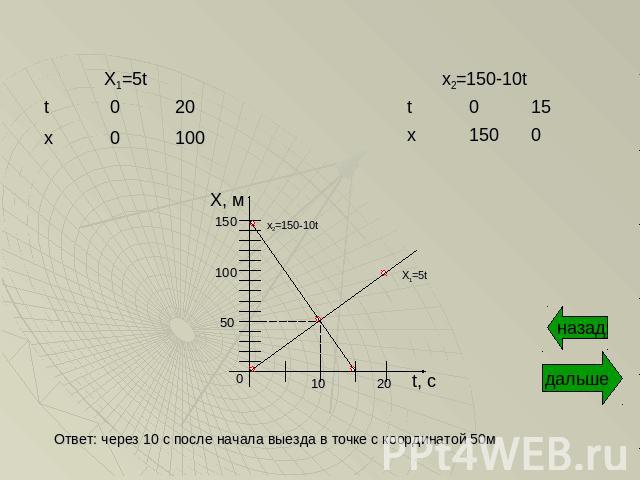
2) x1=5t - движение одного велосипедиста x2=150-10t – движение второго велосипедистаЗадание: построить графики зависимости x(t). Найти время и место встречи.

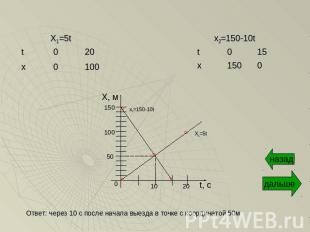
Ответ: через 10 с после начала выезда в точке с координатой 50м

Перемещение при равноускоренном движении

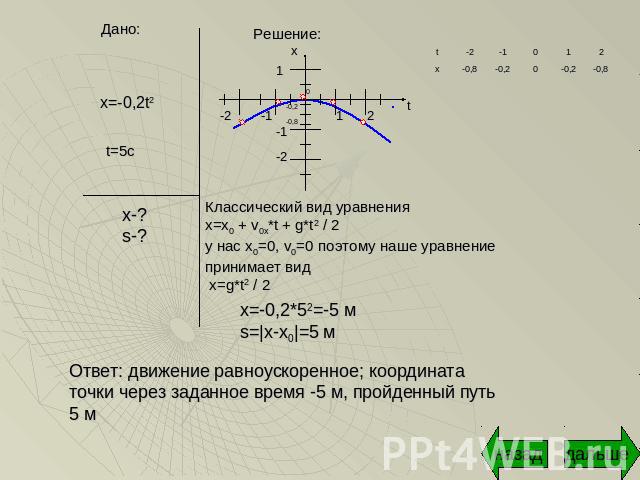
1) Уравнение движения материальной точки имеет вид х=-0,2t2. Какое это движение? Найти координату точки через 5 с и путь, пройденный ею за это время. Построить график зависимости х от t.

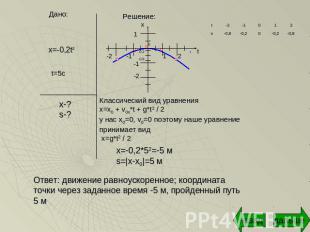
Классический вид уравненияx=x0 + v0x*t + g*t2 / 2у нас х0=0, v0=0 поэтому наше уравнение принимает вид x=g*t2 / 2 х=-0,2*52=-5 мs=|x-х0|=5 м Ответ: движение равноускоренное; координата точки через заданное время -5 м, пройденный путь 5 м

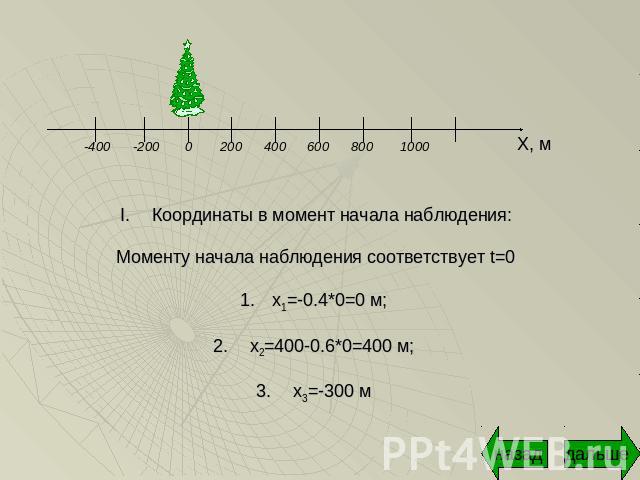
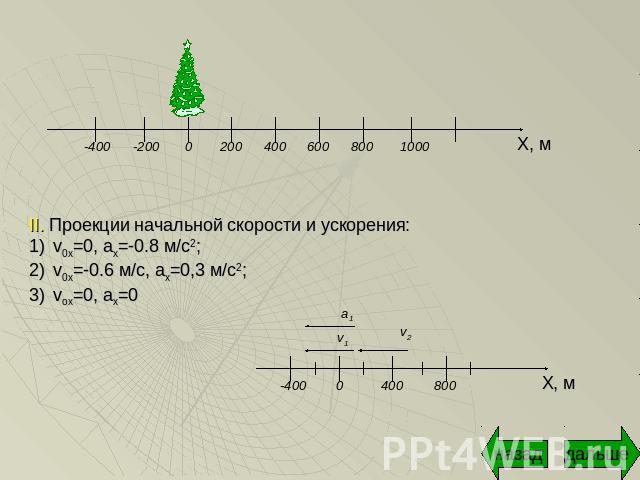
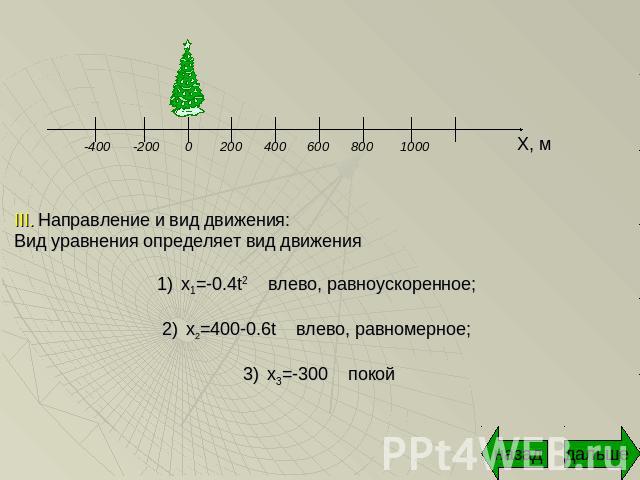
2) Уравнения движения по шоссе велосипедиста, бензовоза и пешехода имеют вид: x1=-0.4t2, x2=400-0.6t и x3=-300 соответственно. Найти для каждого из тел: координату в момент начала наблюдения, проекции начальной скорости и ускорения, а также направление и вид движения.

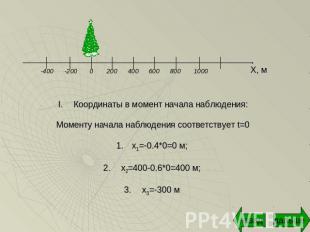
Координаты в момент начала наблюдения:Моменту начала наблюдения соответствует t=0x1=-0.4*0=0 м; x2=400-0.6*0=400 м; x3=-300 м

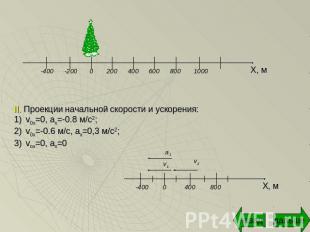
II. Проекции начальной скорости и ускорения:v0x=0, ax=-0.8 м/с2; v0x=-0.6 м/с, ах=0,3 м/с2; vox=0, ax=0

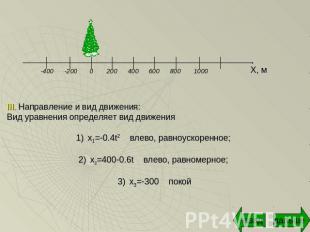
III. Направление и вид движения:Вид уравнения определяет вид движенияx1=-0.4t2 влево, равноускоренное; x2=400-0.6t влево, равномерное; x3=-300 покой

3) Движения двух автомобилей по шоссе заданы уравнениями х1=2t+0.2t2 и х2=80-4t. Описать картину движения. Найти: а) время и место встречи автомобилей; б) расстояние между ними через 5 с от начала отсчета времени; в) координату первого автомобиля в тот момент времени, когда второй находился в начале отсчета.

ДаноРешение По виду самих уравнений определяем, что первый движется ускоренно, а второй равномерно. а) поскольку во время встречи координаты обоих автомобилей будут равны х1=х2 2t+0.2t2=80-4t 0.2t2+6t-80=0 t=10 cтеперь в одно из уравнений можно подставить найденное только что время tx=80-4*10=40 м б) х1=2*5+0.2*52=15 м х2=80-4*5=60 м х2 - х1=60-15=45 м в) х2=0 => 0=80-4*t => t=20 х1=2*20+0,2*202=120 м

Многие школьные предметы перекликаются друг с другом, например, такие как физика и математика. Именно поэтому важно знать как решается то или иное уравнение в математике, что бы не допустить ошибки в физике.