Презентация на тему: Изучение сечений в стереометрии с помощью компьютера

Ямало-Ненецкий автономный округ г. Губкинский средняя школа № 4 Изучение сеченийв стереометриис помощью компьютера

В школьном курсе стереометрии основными задачами на построение являются задачи на построение сечений пространственных фигур, а для этого необходимо научиться изображать эти фигуры.

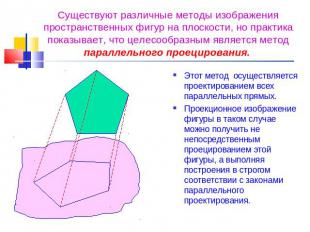
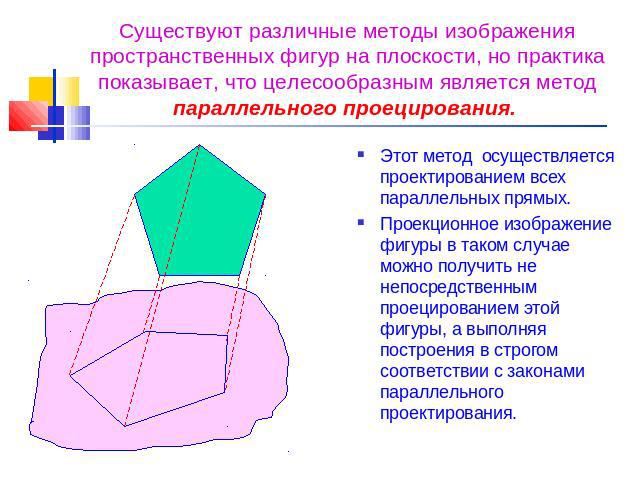
Существуют различные методы изображения пространственных фигур на плоскости, но практика показывает, что целесообразным является метод параллельного проецирования. Этот метод осуществляется проектированием всех параллельных прямых. Проекционное изображение фигуры в таком случае можно получить не непосредственным проецированием этой фигуры, а выполняя построения в строгом соответствии с законами параллельного проектирования.

Эти законы сводятся к сохранению на проекционном чертеже таких свойств фигуры: 1. свойство фигуры быть точкой, прямой, плоскостью; 2. свойство фигуры иметь пересечение; 3. деление отрезка в данном отношении; 4. свойство прямых (плоскостей, прямой и плоскости) быть параллельными; 5. свойство фигуры быть треугольником, параллелограммом, трапецией; 6. отношение длин параллельных отрезков; 7. отношение площадей двух фигур.

В зависимости от цели используются изображения следующих трех видов: иллюстративные полные метрически определенные Но всем этим изображениям предъявляются такие требования: a) изображение должно быть верным, то есть оно должно представлять собой фигуру, подобную произвольной параллельной проекции; b) изображение должно быть по возможности наглядным, то есть должно вызывать верные пространственные представления об изображаемой фигуре; c) изображение должно быть легко выполнимым, то есть правила построения должны быть максимально простыми; d) изображение должно быть удобоизмеримым, то есть по изображению можно, и притом не сложно, восстановить оригинал метрически точно. Только после того можно строить их сечения.

Цели моей работы: исследовать построение сечений в стереометрии и применить компьютер для изображения сечений. При решении стереометрических задач требования к качеству чертежа, его наглядности значительно возрастает. В построение пространственного чертежа входит: - выбор оптимального положения изображаемого тела, - выбор ракурса и проекции, - умение минимизировать количество изображенных линий, - умение строить сечения и проекции на плоскость, - умение перевести условия задачи на графический язык.

Пространственные тела можно разделить на две группы: удобные для пространственного изображения К первой группе относятся следующие многогранники: - параллелепипед (прежде всего прямоугольный), - треугольная пирамида (тетраэдр) - треугольная призма, - четырехугольная пирамида. и неудобные. Ко второй группе относятся: Конечно, такое разделение носит условный характер. И одной из целей данной исследовательской работы является построение сечения в «неудобных» для изображения пространственных тел.

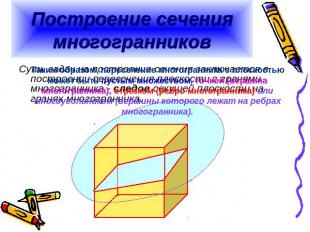
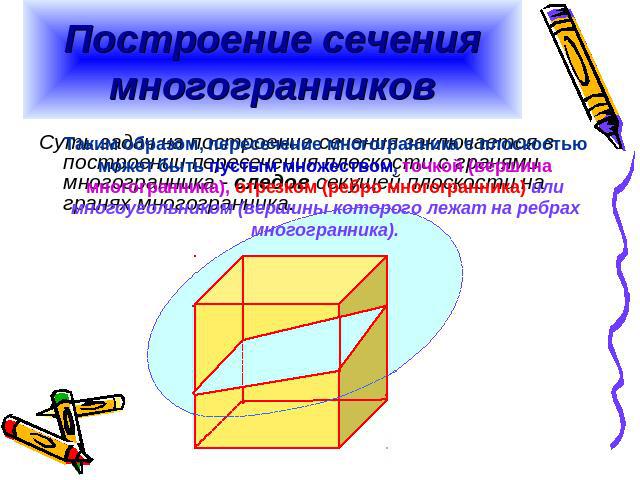
Построение сечения многогранников Таким образом, пересечение многогранника с плоскостью может быть пустым множеством, точкой (вершина многогранника), отрезком (ребро многогранника) или многоугольником (вершины которого лежат на ребрах многогранника).

Построение следов плоскости на гранях можно вести по одному из следующих приемов: а) строить следы прямых , лежащих в плоскости сечения, и по ним находить следы самой плоскости;б) строить третий след трехгранного угла по двум найденным следам на плоскости сечения;в) применить внутреннее проектирование. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.

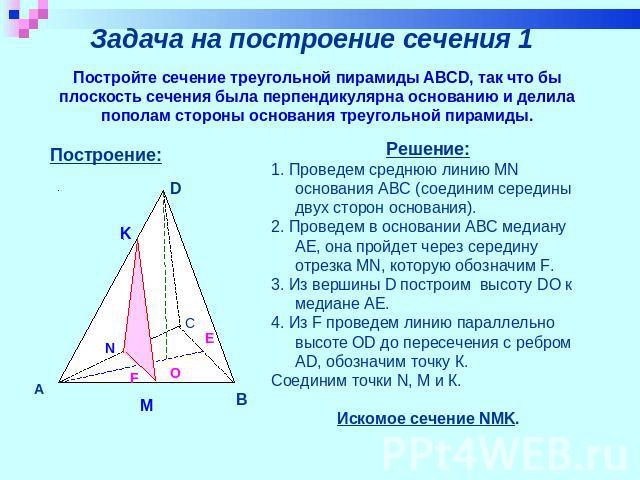
Задача на построение сечения 1 Постройте сечение треугольной пирамиды ABCD, так что бы плоскость сечения была перпендикулярна основанию и делила пополам стороны основания треугольной пирамиды. Решение:1. Проведем среднюю линию MN основания ABC (соединим середины двух сторон основания). 2. Проведем в основании ABC медиану AE, она пройдет через середину отрезка MN, которую обозначим F.3. Из вершины D построим высоту DO к медиане AE.4. Из F проведем линию параллельно высоте OD до пересечения с ребром AD, обозначим точку К. Соединим точки N, М и К. Искомое сечение NMK.

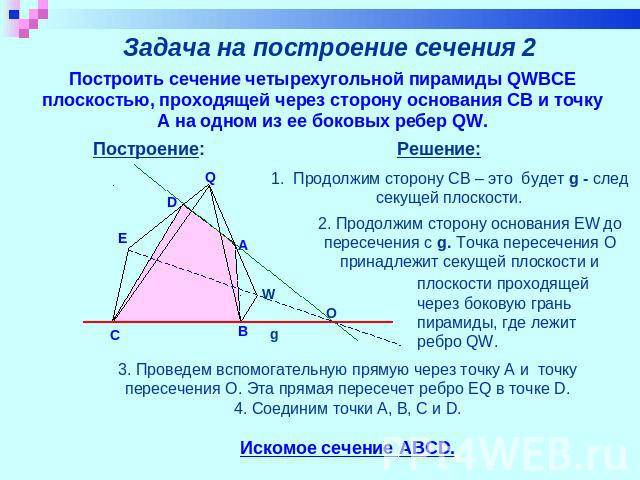
Задача на построение сечения 2 Построить сечение четырехугольной пирамиды QWBCE плоскостью, проходящей через сторону основания CB и точку А на одном из ее боковых ребер QW. Решение: 1. Продолжим сторону CB – это будет g - след секущей плоскости. 2. Продолжим сторону основания EW до пересечения с g. Точка пересечения О принадлежит секущей плоскости и плоскости проходящей через боковую грань пирамиды, где лежит ребро QW. 3. Проведем вспомогательную прямую через точку А и точку пересечения О. Эта прямая пересечет ребро EQ в точке D.4. Соединим точки A, B, C и D.Искомое сечение ABCD.

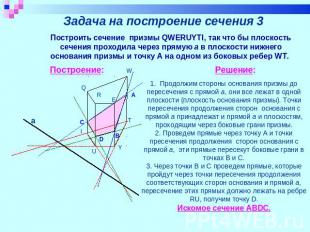
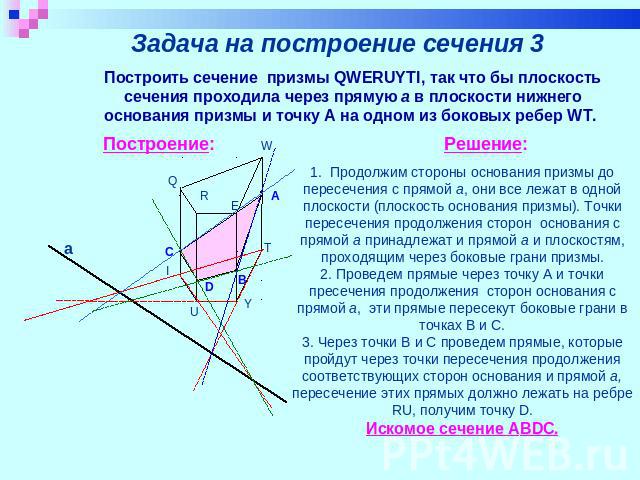
Задача на построение сечения 3 Построить сечение призмы QWERUYTI, так что бы плоскость сечения проходила через прямую a в плоскости нижнего основания призмы и точку A на одном из боковых ребер WT. 1. Продолжим стороны основания призмы до пересечения с прямой а, они все лежат в одной плоскости (плоскость основания призмы). Точки пересечения продолжения сторон основания с прямой а принадлежат и прямой а и плоскостям, проходящим через боковые грани призмы.2. Проведем прямые через точку А и точки пресечения продолжения сторон основания с прямой а, эти прямые пересекут боковые грани в точках В и С.3. Через точки В и С проведем прямые, которые пройдут через точки пересечения продолжения соответствующих сторон основания и прямой а, пересечение этих прямых должно лежать на ребре RU, получим точку D.Искомое сечение АBDC.

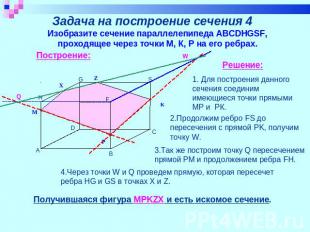
Задача на построение сечения 4 Изобразите сечение параллелепипеда ABCDHGSF, проходящее через точки М, К, Р на его ребрах. Решение: 1. Для построения данного сечения соединим имеющиеся точки прямыми МР и РК. 2.Продолжим ребро FS до пересечения с прямой PK, получим точку W. 3.Так же построим точку Q пересечением прямой PM и продолжением ребра FH. 4.Через точки W и Q проведем прямую, которая пересечет ребра HG и GS в точках X и Z. Получившаяся фигура MPKZX и есть искомое сечение.

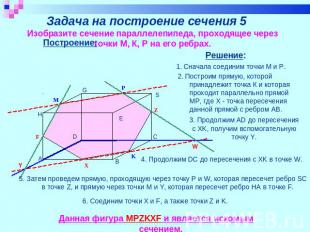
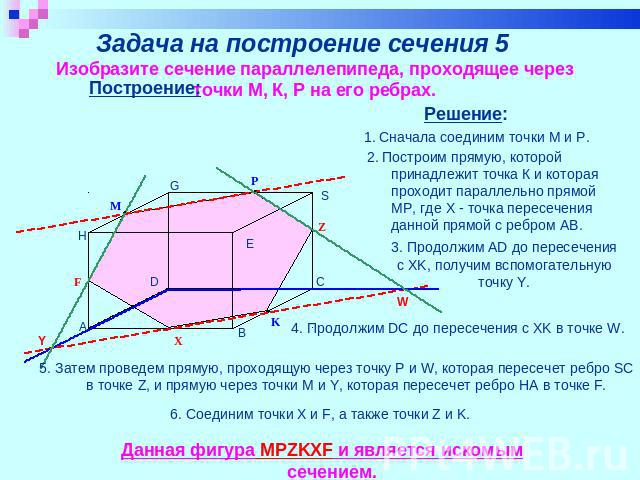
Задача на построение сечения 5 Изобразите сечение параллелепипеда, проходящее через точки М, К, Р на его ребрах. Построение: 2. Построим прямую, которой принадлежит точка К и которая проходит параллельно прямой МР, где Х - точка пересечения данной прямой с ребром АВ. 3. Продолжим AD до пересечения с XK, получим вспомогательную точку Y. 5. Затем проведем прямую, проходящую через точку Р и W, которая пересечет ребро SС в точке Z, и прямую через точки M и Y, которая пересечет ребро HA в точке F. 6. Соединим точки X и F, а также точки Z и K. Данная фигура MPZKXF и является искомым сечением.

Задача на построение сечения 6 Построить сечение призмы ABCDFEGHKL плоскостью, проходящей через три произвольные точки X, Y и Z на поверхности (не на ребрах) призмы. 2. На плоскости нижнего основания построим проекции прямых ZY и ZX, пересечение прямых со своими проекциями обозначим М и N. 3. Проведем прямую MN, являющуюся пересечением плоскости нижнего основания и секущей плоскости. 4. Построим продолжение ребра LK до пересечения с прямой MN, из точки пересечения проведем прямую через точку Z, которая пересечет ребра призмы в точках 1 и 2. Получим сторону сечения 12. Также найдем стороны сечения 23, 34 и 45. Получили искомое сечение 12345.

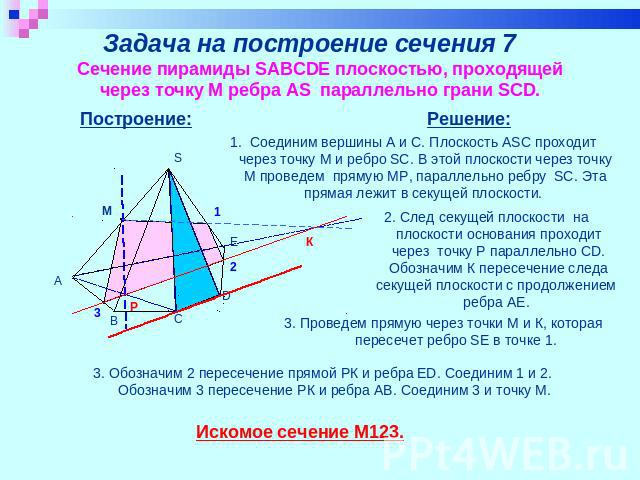
Задача на построение сечения 7 Сечение пирамиды SABCDE плоскостью, проходящей через точку M ребра AS параллельно грани SCD. 1. Соединим вершины А и С. Плоскость ASC проходит через точку М и ребро SC. В этой плоскости через точку М проведем прямую МР, параллельно ребру SC. Эта прямая лежит в секущей плоскости. 2. След секущей плоскости на плоскости основания проходит через точку Р параллельно CD. Обозначим К пересечение следа секущей плоскости с продолжением ребра АЕ. 3. Проведем прямую через точки М и К, которая пересечет ребро SЕ в точке 1. 3. Обозначим 2 пересечение прямой РК и ребра ED. Соединим 1 и 2. Обозначим 3 пересечение РК и ребра AB. Соединим 3 и точку М. Искомое сечение М123.

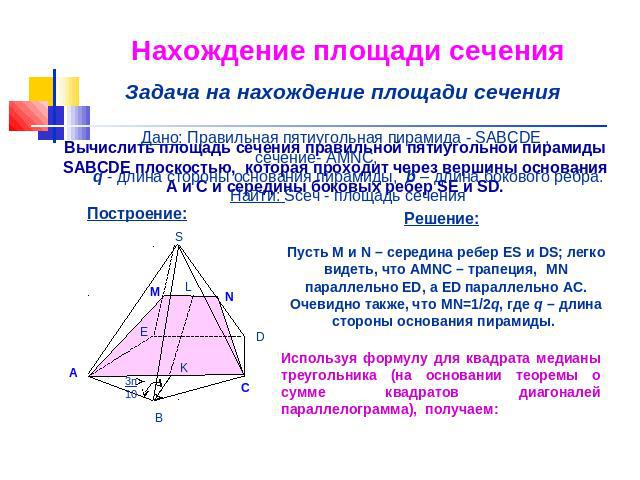
Нахождение площади сечения Задача на нахождение площади сечения Дано: Правильная пятиугольная пирамида - SABCDE , сечение- AMNC, q - длина стороны основания пирамиды, b – длина бокового ребра.Найти: Sсеч - площадь сечения Пусть M и N – середина ребер ES и DS; легко видеть, что AMNC – трапеция, MN параллельно ED, а ED параллельно AC. Очевидно также, что MN=1/2q, где q – длина стороны основания пирамиды. Используя формулу для квадрата медианы треугольника (на основании теоремы о сумме квадратов диагоналей параллелограмма), получаем:

Нахождение площади сечения Задача на нахождение площади сечения Дано: Правильная пятиугольная пирамида - SABCDE , сечение- AMNC, q - длина стороны основания пирамиды, b – длина бокового ребра.Найти: Sсеч - площадь сечения KL - отрезок соединяющий середину трапеции ACNM Таким образом , искомая площадь Sсеч =1/2∙(MN+AC)KL=(2+ 5)∙ 4b2 + 3q2

Исследовательская задача построения сечения вмногограннике Рассматривая тему сечения в стереометрии, я выяснила, какие бывают задачи на построение и вычисления площади сечения в многоугольниках. Проводя исследовательскую работу, я заинтересовалась, как будет выглядеть сечение в более сложной фигуре, например, в додекаэдре, и решила построить данное сечения сама.

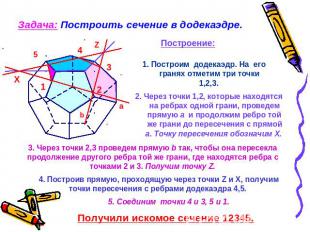
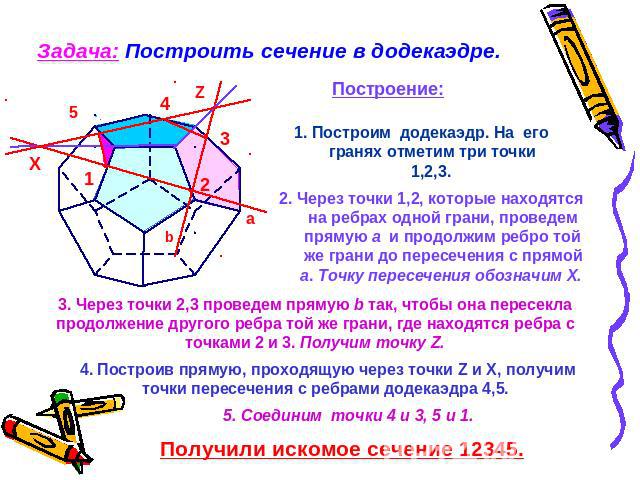
Задача: Построить сечение в додекаэдре. 1. Построим додекаэдр. На его гранях отметим три точки 1,2,3. 2. Через точки 1,2, которые находятся на ребрах одной грани, проведем прямую а и продолжим ребро той же грани до пересечения с прямой а. Точку пересечения обозначим Х. 3. Через точки 2,3 проведем прямую b так, чтобы она пересекла продолжение другого ребра той же грани, где находятся ребра с точками 2 и 3. Получим точку Z. 4. Построив прямую, проходящую через точки Z и X, получим точки пересечения с ребрами додекаэдра 4,5. 5. Соединим точки 4 и 3, 5 и 1. Получили искомое сечение 12345.

Задачи по геометрии и особенно по стереометрии часто трудны для понимания школьников по причине сложности изображения пространственных фигур на плоском чертеже. Не всегда школьникам хватает воображения и пространственного видения геометрических тел для правильного построения заданных фигур. А чертить на бумаге приходится с помощью только линейки и карандаша. Не получился чертеж, выбран неудачный ракурс, не вышли параллельные линии, и начинай всё сначала!

И здесь на помощь приходят современные компьютерные технологии. Стереометрия развивает логику, пространственное воображение. Я убедилась, что с помощью компьютера можно наглядней изучить эту науку, лучше научилась рассуждать и понимать условия задач, анализировать и творчески подходить к решению поставленных задач.

Изучение сечений в стереометрии с помощью компьютера Чемизова Алена Олеговна г.Губкинский 2006г.