Презентация на тему: Системы двух линейных уравнений с двумя переменными

Учиться, учиться и ещё раз учиться! «СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ» Презентация БЕЛОУСОВА ИЛЬИ

Решить уравнение:

Метод подстановки: Итак, сможете назвать алгоритм решения системы двух уравнений с двумя переменными методом подстановки?

Решаем вместе! Решить уравнение методом подстановки. Делаем вместе, всё по порядку!1) Выразим в первом уравнении y через x: 2)Подставим полученное на первом шаге выражение вместо y во второе уравнение системы:3)Решить полученное на втором шаге уравнение относительно x:4)Подставить найденное на третьем шаге значение x в выражениеy через x, полученное на первом шаге.

Решить систему уравнений: 1)Чтобы решить эту систему,нам нужно убрать y (игреки).Для этого y(игреки) должны быть равны(допустим 2y и 2y или 7y и 7y).Вычтем второе уравнение из первого:2) Подставим найденное значение x=2 в первое уравнение заданной системы, т.е. в уравнение 2x+3y=1 3)Пара x=2, y=-1 – решение заданной системыОтвет: (2;-1)

А теперь решим вот такое уравнение методом АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ!1)Здесь сразу исключить переменную x или переменную y из обоих уравнений с помощью сложения или вычитания уравнений не удастся.Давайте умножим все члены второго уравнения на два! И посмотрим что получится!2) Да, да теперь с помощью вычитания можно убрать X.Подставим y в первое или во второе уравнение и запишем ответ! Ответ: (-0,25 ; 0)

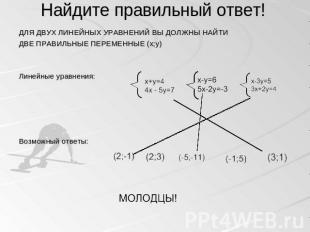
Найдите правильный ответ! ДЛЯ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ ВЫ ДОЛЖНЫ НАЙТИ ДВЕ ПРАВИЛЬНЫЕ ПЕРЕМЕННЫЕ (x;y) Линейные уравнения:Возможный ответы:

Найдите ответ!

Найдите ответ! Ответы все не подходят! Правильный???(-6;5)

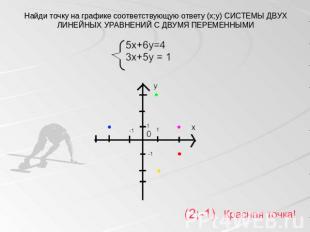
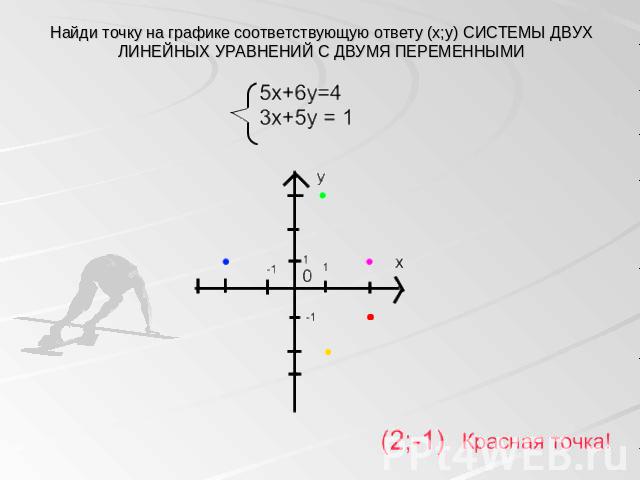
Найди точку на графике соответствующую ответу (x;y) СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ