Презентация на тему: Решение геометрических задач с практическим содержанием

Малиновоозерская муниципальная средняя общеобразовательная школа Решение геометрических задач с практическим содержанием. Работу выполнила учащаяся 10 класса Белоусова Надежда Анатольевна Руководитель Каланчина Екатерина Фридриховна Малиновое Озеро 2007

План Ι.Вступление. ΙΙ. Основная часть 1.Из истории возникновения геометрии. 2.Методы решения геометрических задач а) геометрический метод б) аналитический метод ΙΙΙ.Заключение

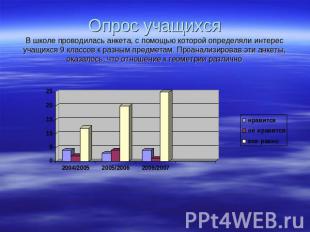
Опрос учащихсяВ школе проводилась анкета, с помощью которой определяли интерес учащихся 9 классов к разным предметам. Проанализировав эти анкеты, оказалось, что отношение к геометрии различно

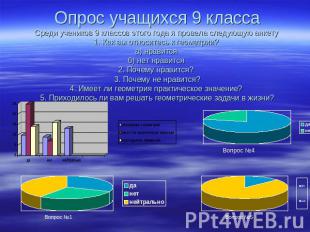
Опрос учащихся 9 классаСреди учеников 9 классов этого года я провела следующую анкету 1. Как вы относитесь к геометрии? а) нравится б) нет нравится 2. Почему нравится? 3. Почему не нравится?4. Имеет ли геометрия практическое значение? 5. Приходилось ли вам решать геометрические задачи в жизни?

Объект исследования – геометрия Предмет исследования - задачи с практическим содержанием. Цель исследования - 1. узнать историю возникновения геометрии. 2. познакомиться с методами решения задач 3. решить задачи с практическим геометрическим содержанием.

Знакомясь с историей возникновения геометрии по различным источникам мне удалось убедиться что геометрия возникла из необходимости практики и служила для решения практических задач. Достаточно назвать следующие имена: Архимед - впервые решил много трудных задач по геометрии: нашел правила вычисления площадей и объемов различных тел, с большой точностью определил отношение длины окружности к ее поперечнику. Эратосфен - впервые определил размеры земного шара. Фалес – когда египтяне задали ему задачу найти высоту одной из громадных пирамид он нашел простое и красивое решение. Пифагор – его наука нашла применение в землемерии. Евклид – написал книгу «Начала» в которой объединил вместе все результаты, полученные многими поколениями ученых.

Геометрический метод. Говоря о методах решения геометрических задач, следует отметить некоторые специфические особенности этих методов: большое разнообразие, взаимозаменяемость, трудность формального описания, отсутствие четких границ области применения. Кроме того, очень часто при решении некоторых достаточно сложных задач приходится прибегать к использованию комбинаций методов и приемов. Геометрический метод характеризуют как метод, идущий от наглядных представлений. Существенными признаками этого понятия являются геометрические (наглядные) представления и законы геометрии, в которых отражены свойства геометрических фигур.

Деревни А и В находятся на одинаковом расстоянии от города М. На прямой, проходящей через М и В, расположены еще две деревни С и D. К какой из первых двух деревень А и В ближе расположена: а) деревня С; б) деревня D? А) Соединив А с точками М и С, видим, что МА + АС > МС, но МА = МВ, следовательно АС>ВС. Поэтому, деревня С расположена ближе к В, чем к А. Б) Соединив А с точкой D, видим, что DМ + МА >DА, но МА = МВ, следовательно, DВ>DА. Поэтому, деревня D расположена ближе к А, чем к В.

Легенда повествует о том, как Фалес сумел измерить расстояние от берега до стоящего в гавани корабля. Решение: В одной из четырех гаваней Милета был построен дальномер, состоящий из трех вбитых в землю колышков А, В, С (АВ = ВС) и размеченной прямой СК ┴ СА. При появлении корабля на прямой СК находили такую точку D, чтобы точки D, В и Е оказывались на одной прямой. Тогда расстояние CD на суше было искомым расстоянием АЕ до корабля. Я думаю, что эту задачу можно решить и так, чтобы занять меньше площади на суше: если СВ будет меньше АВ в 2 раза, то ∆BDC подобен ∆BAE, тогда CD будет в 2 раза меньше чем АЕ.

Аналитический метод решения. Для этого метода характерны формулы, уравнения. Говоря об этом алгебраическом методе решения геометрических задач, выделим, прежде всего, две его разновидности: а) метод поэтапного решения; б) метод составления уравнений. Сущность первого метода коротко состоит в следующем. Величины, заданные в условии задачи, и те, которые нужно найти, мы связываем цепочкой промежуточных величин, каждая из которых последовательно определяется через предыдущие. Полезно при этом сначала составить план решения задачи, другими словами, выписать цепочку элементов, которые можно последовательно вычислить, соединяющую то, что дано, и то, что нужно найти. Алгебраический метод трактуется как метод, заключающийся в употреблении букв и буквенных выражений, над которыми по определенным правилам производятся преобразования. Его называют еще методом буквенных вычислений.

Колодец цилиндрической формы, имеющий в диаметре 135 см., а глубину 180 см., надо выложить кирпичом. Сколько штук кирпича для этого потребуется, если размер кирпича 25х12х6,5 см. Решение: Длина окружности, диаметр которой меньше диаметра колодца на удвоенную ширину кирпича, равна dπ ≈ 499 см. Длину окружности делим на длину кирпича, получаем 499 : 25 ≈ 20 кирпичей уложено в один ряд. Таких рядов будет 180 : 6,5 ≈ 28. Следовательно, потребуется кирпича 20 · 28 = 560 штук. Ответ: 560 кирпичей.

Использование недр связано с ежегодным извлечением около 150 млрд. т горных пород. Но лишь их незначительная часть реализуется в виде продукции производства, а остальное превращается в отходы. Какова высота горы отходов, если считать, что эта гора имеет форму конуса, высота которого равна радиусу основания. При добыче 1 т руды получается 1,05 м3 отходов. Решение: Вычислим сначала объем V конуса отвалов: V = 150 (млрд. т.) · 1,05 (м3) = 157,5 Млрд. м3). Объем V конуса с основанием S, радиусом основания h и высотой h равен V = 1/3Sh = 1 : 3πh3 . Отсюда h3 = 3V : π = 3 · 157,5 (млрд. м3)/π, h = 3√ 150 500 000 000 (м3) ≈ 5,32 (тыс. м) = 5320 (м).

В нашем поселке Малиновое Озеро Алтайского края предприятием «Алтайсода» используется местное сырье. Соду добывают из озера и складывают ее в виде пирамиды на площадку для дальнейшего использования. Каков объем добытого сырья, расположенного между старым и новым заводом? Для этого измерим длину l = 79 м, ширину d = 8,1м основания пирамиды и ее высоту h = 4 м Решение: V = 1/3 ∙ l ∙ d ∙ h V =1/3 ∙ 79 ∙ 8 ∙ 4 = 853 м3 Ответ: V = 853 м3.

Заключение В ходе исследования я познакомилась с историей возникновения геометрии. И узнала, что геометрия возникла очень давно. И нужна она не столько как просто наука, а как инструмент для решения практических задач. Также изучение этой темы и наблюдение за окружающей действительностью позволило мне убедиться в практической значимости математики.

Литература Атасян Л.С. Геометрия 7 – 9 класс «Специальная литература» Москва «Просвещение» 2003 Варданян С.С. Задачи по планиметрии с практическим содержанием Москва «Просвещение» 1989 Глейзер Г.И. История математики в школе 7 – 8 классы Москва «Просвещение» 1982 Депман И.Я., Виленкин Н.Я. За страницами учебника математики Москва «Просвещение» 1989 Феоктистов И. Геометрия до Евклида в очерках и задачах Москва «Чистые пруды» 2005 Шарыгин И.Ф. Факультативный курс по математике Решение задач Москва «Просвещение» 1989 Долгорукова Наталья 9 класс Руководитель Булдакова Светлана Геннадьевна // «Портфолио» Фестиваль исследовательских и творческих работ учащихся 2005/2006 учебный год