Презентация на тему: Равновеликие и равносоставленные плоские фигуры

Равновеликие и равносоставленные плоские фигуры

Два множества называются равномощными, если между ними можно установить взаимнооднозначное соответствие.



Изучение и использование понятия и свойств равновеликих и равносоставленных фигур в практической деятельности.

Задачи: Изучить определения и свойства равновеликих и равносоставленных плоских геометрических фигур;Доказать свойство равновеликости равносоставленных фигур;Исследовать практическую значимость равновеликих и равносоставленных фигур.

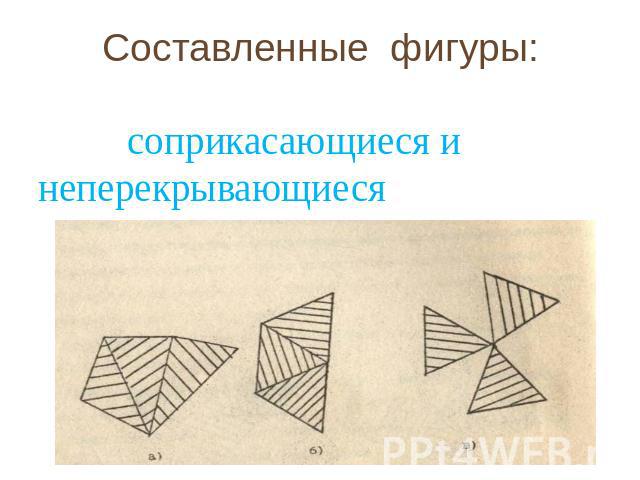
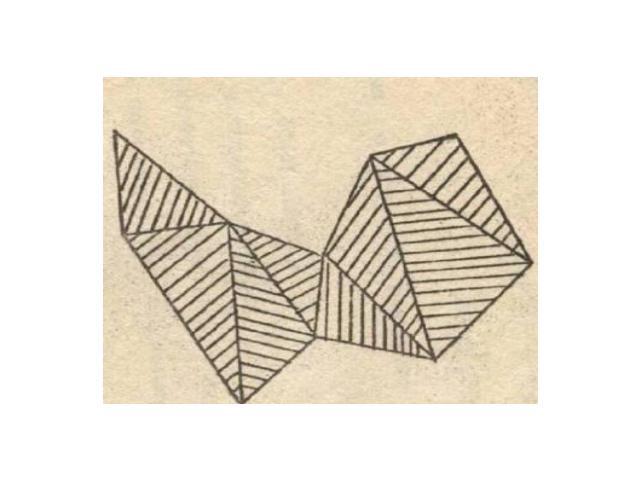
Составленные фигуры: соприкасающиеся и неперекрывающиеся


Теорема Л. Эйлера Всякий выпуклый n-угольник можно разбить непересекающимися диагоналями на треугольники k- способами, k = 2∙ 6 ∙ 10 … (4n -10) ( n -1) ! , где n- есть натуральное число, n > 2.

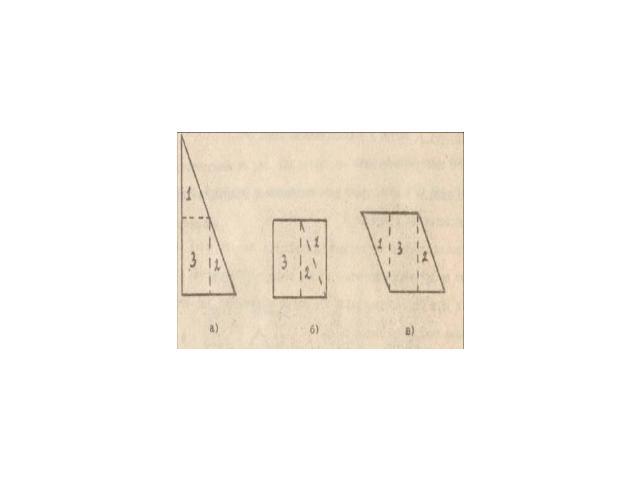
а) n =3, k = 2 / (3-1)! = 2 / 2! = 2 / 1· 2 = 1б) n =4, k = 2 ∙ 6 / (4 - 1)! = 12 / 3! = 12 / 1 · 2 · 3 = 2в) n =4, k = 2 ∙ 6 ∙10 / (5- 1)! = 120 / 1 ∙ 2· 3∙ 4 = 5г) n =6, k = 2 ∙ 6 ∙10 · 14 / ( 6-1)! =14д) n =7, k = 2 ∙ 6 ∙10 · 14 ∙ 18 / ( 7-1)! = 42


Теорема Площади равных многоугольников равны.


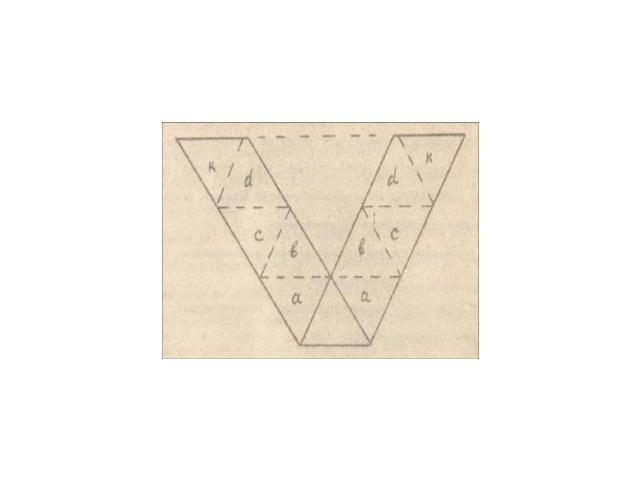
Определение Многоугольники P и Q равносоставлены, если их можно разбить на соответственно равные фигуры

Криволинейные фигуры

Свойства равносоставленных фигур1. Фигура P равносоставлена самой себе.

2. Если фигура P равносоставлена с фигурой Q, то фигура Q равносоставлена с фигурой P

3. Если фигура P равносоставлена с фигурой Q, а фигура Q равносоставлена с фигурой F, то фигура P равносоставлена с фигурой F


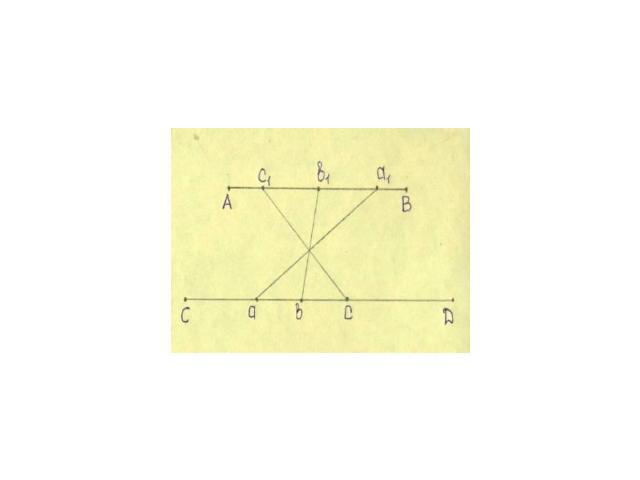
Дано: P и Q равносоставленные многоугольникиДоказать: P и Q равновеликиДоказательство: P = P₁+ P₂ + … +PnQ = Q₁ + Q₂ + … +Qn, где P₁=Q₁, P₂ = Q₂, …, Pn = Qn.Sp₁ = SQ₁, Sp₂ = SQ₂, …, Spn = SQn. Sp = Sp₁ + Sp₂ + … + Spn = SQ₁+ SQ₂ + … + SQn = SQ. P и Q равновелики .

Всякие равносоставленные многоугольники равновелики.

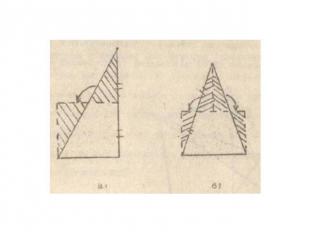

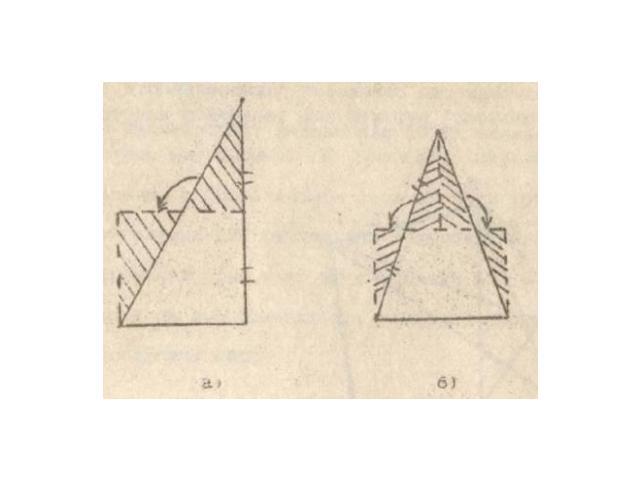
Равновеликие многоугольники равносоставленны

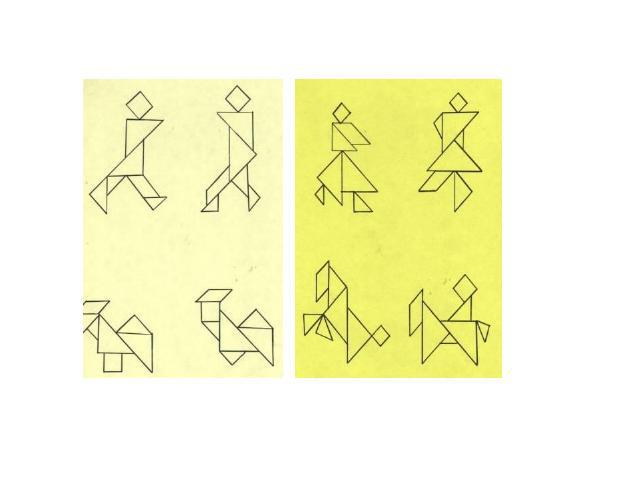
Игра «Танграм»
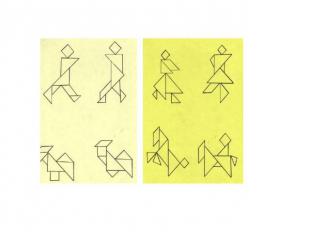


Витраж - картина, узор из цветного стекла.

Год 1957.Морис Эшер Писал о взаимосвязи математической науки со своим творчеством: