Презентация на тему: Пятый постулат Евклида. Неевклидова геометрия

Исследовательская работа.Пятый постулат Евклида. Неевклидова геометрия

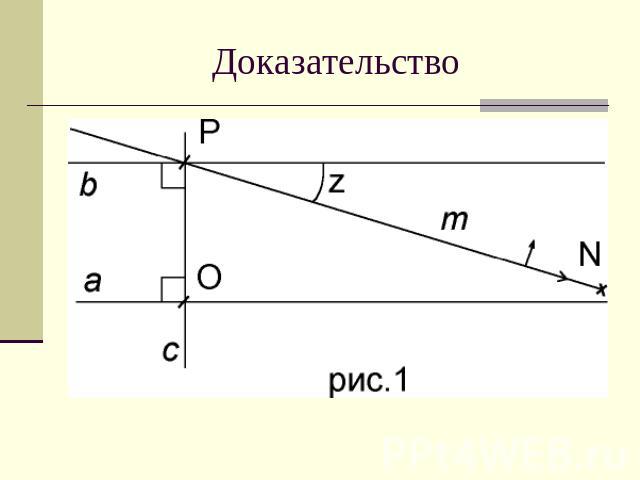
ВведениеЕсли две прямые, лежащие в одной плоскости, пересечены третьей и если сумма внутренних односторонних углов меньше двух прямых углов, то эти прямые пересекутся с той стороны, где это имеет место.

Евклид

Адриен Мари Лежандр

Карл Фридрих Гаусс

Янош Бояи (Больяй)

Геометрия Лобачевского

АксиомаЧерез точку, лежащую вне прямой в плоскости, определяемой ими, можно провести не менее двух прямых, не пересекающих данную прямую.

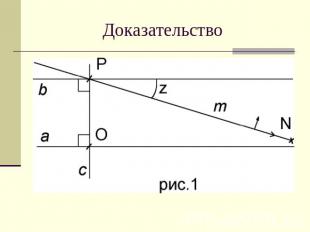
Доказательство

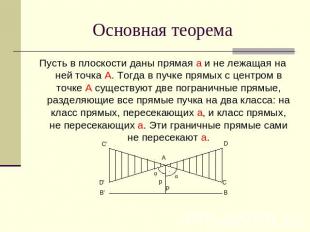
Основная теорема Пусть в плоскости даны прямая a и не лежащая на ней точка A. Тогда в пучке прямых с центром в точке A существуют две пограничные прямые, разделяющие все прямые пучка на два класса: на класс прямых, пересекающих a, и класс прямых, не пересекающих a. Эти граничные прямые сами не пересекают a.

Определение Прямая C'C называется параллельной прямой B'B в направлении B'B в точке A, если, во-первых, прямая C'C не пересекает прямой BB', во-вторых, C'C является граничной в пучке прямых с центром в точке A, то есть всякий луч AE, проходящий внутри угла CAD, где D – любая точка прямой BB', пересекает луч DB.

Сферическая геометрияОпределение 1 Большим кругом называется часть плоскости, которая проходит через центр сферы.Определение 2 Любая плоскость, которая не проходит через центр сферы, называется малым кругом.

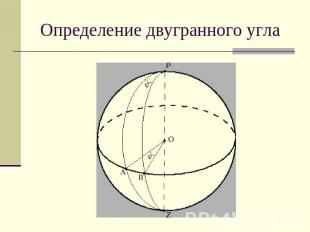
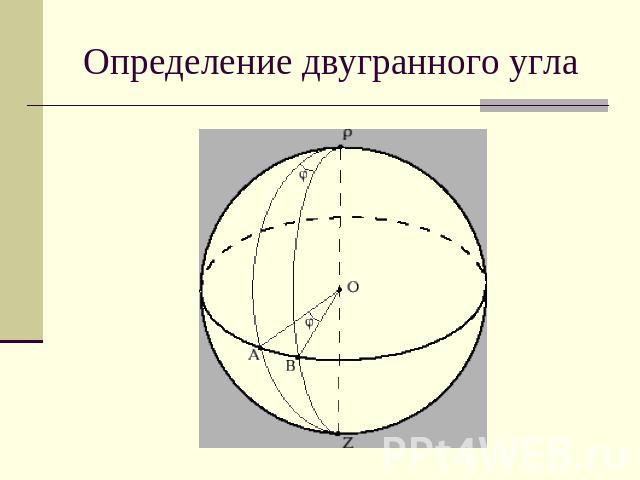
Определение двугранного угла

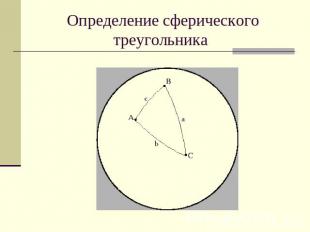
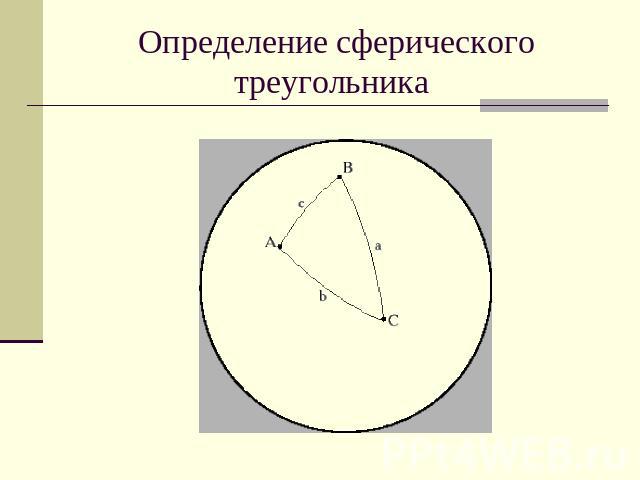
Определение сферического треугольника

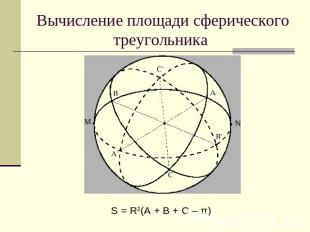
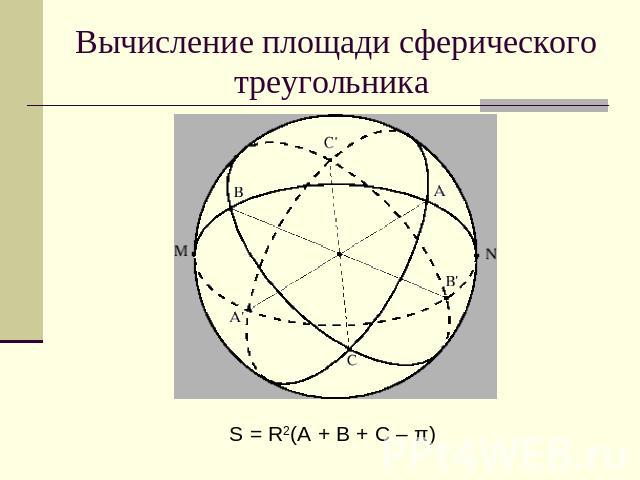
Вычисление площади сферического треугольника S = R2(A + B + C – π)

Заключение

Благодарю за внимание!