Презентация на тему: Свойства и график функции y=sinx

Свойства функций Область значений функции Периодичность Четность, нечетность Промежутки знакопостоянства Промежутки монотонности Наибольшее (наименьшее) значение функции Нули функции Область определения функции

х у 0 0 2π 1 -1 D(у)=(- ; + ) Е(у)= [-1; 1] Область определения Область значения функции

Периодичность, чётность/нечётность х у 0 0 М у 3 2 z sin (x +2 n) = sin х, n sin (-х) = - sin х f (-х) = - f (х) Функция нечетная f (х +Т) = f (х –Т) = f (х) Функция периодическая -у α - α

Наибольшее и наименьшее значение функции. Нули функции. Промежутки знакопостоянства. y>0 при 0 < x < π y>0 при х (2πn; π+2πn), n z y

Промежутки монотонности у 2 π х 0 0 π -π - 2 π π 2 3 у 1 у 2 М 1 М 2 Функция возрастает на - /2 + 2 n; /2 + 2 n , n Функция убывает на /2 + 2 n; 3 /2 + 2 n , n Z Z х1 х2 I х 1 х 2 IV х 1 х 2 sin х 1 sin х 2 II х 1 х 2 sin х1 sin х 2 III х 1 х 2 sin х 1 sin х 2 sin х 1 sin х2

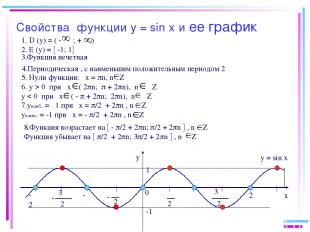
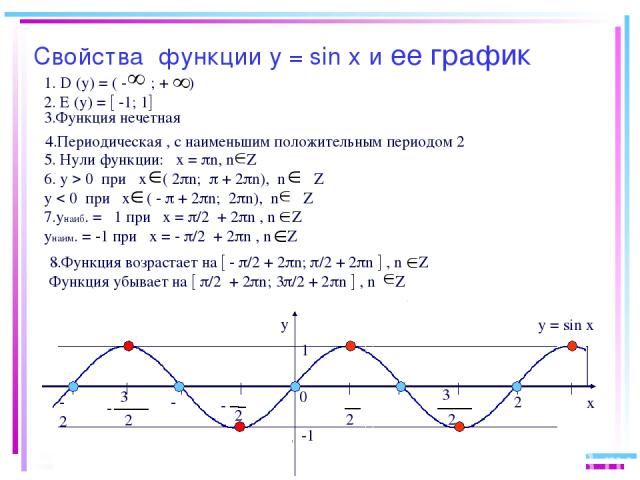
Свойства функции у = sin х и ее график y x 0 2 π 2 π - - -π π 2π -2π 1 -1 1. D (у) = ( - ; + ) 2. Е (у) = -1; 1 5. Нули функции: х = n, n Z 6. у 0 при х ( 2 n; + 2 n), n Z у 0 при х ( - + 2 n; 2 n), n Z 7.унаиб. = 1 при х = /2 + 2 n , n Z унаим. = -1 при х = - /2 + 2 n , n Z y = sin x 4.Периодическая , с наименьшим положительным периодом 2π 3.Функция нечетная 8.Функция возрастает на - /2 + 2 n; /2 + 2 n , n Z Функция убывает на /2 + 2 n; 3 /2 + 2 n , n Z

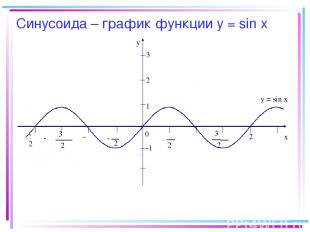
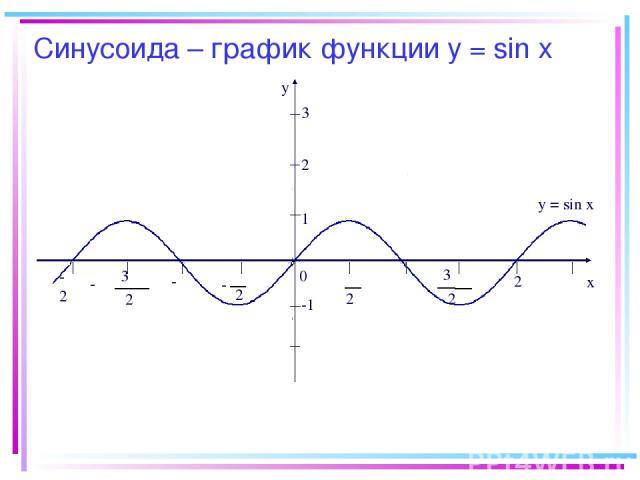
Синусоида – график функции у = sin х -2π y x 0 2 π 2 π - π 2 3 π 2 3 - -π π 2π 1 -1 y = sin x 2 3

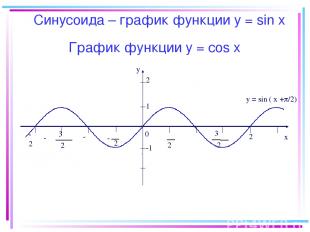
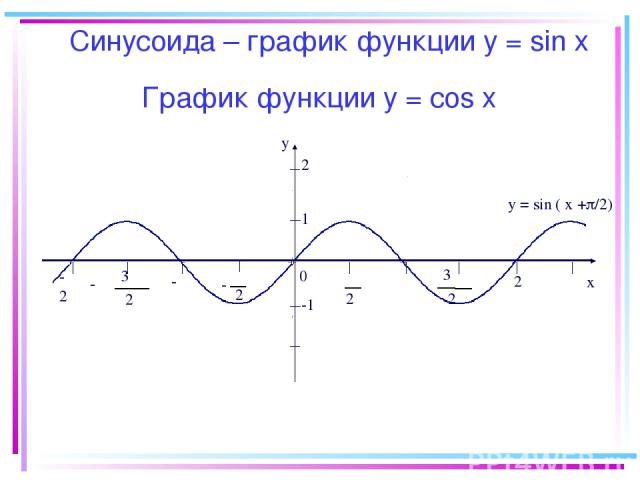
График функции y = соs x -2π y x 0 2 π 2 π - π 2 3 π 2 3 - -π π 2π 1 -1 y = sin ( x + /2) 2 Синусоида – график функции у = sin х

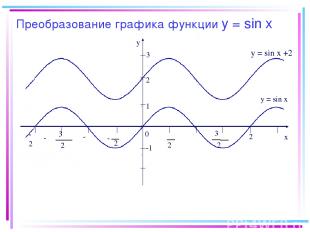
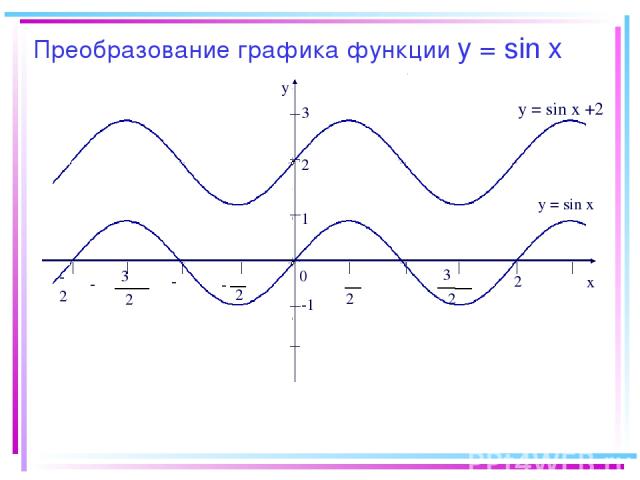
Преобразование графика функции y = sin x -2π y x 0 2 π 2 π - π 2 3 π 2 3 - -π π 2π 1 -1 y = sin x y = sin x +2 2 3