Презентация на тему: Начальные понятия планиметрии. Прямая и отрезок. Луч и угол

«Начальные понятия планиметрии. Прямая и отрезок. Луч и угол» Разработка урока по геометрии 7 класса Учитель математики ГОУ ТО «ПКШ» Журавлева И.А.

Геометрия в переводе с греческого «землемерие» («гео»- по-гречески земля, а «метрео» - мерить) Первым, кто начал получать геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (6 в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном геометрическом языке называется движением.

Наибольшее влияние на все последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в 3 в. до н. э. Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой изучали геометрию. В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука.

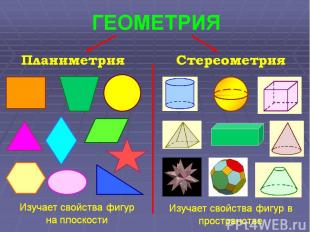
В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, плотности, цвета и т. д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы получаем понятие геометрической фигуры. На уроках математики вы познакомились с некоторыми геометрическими фигурами и представляете себе, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга.

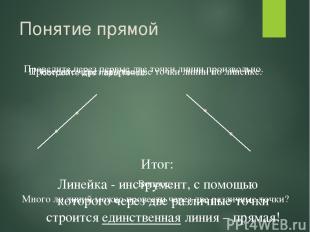
Понятие прямой Постройте две пары точек. Итог: Линейка - инструмент, с помощью которого через две различные точки строится единственная линия – прямая! Проведите через первые две точки линии произвольно. Проведите через вторые две точки линии по линейке. Вопрос: Много ли линий можно провести через две различные точки?

Свойства прямой Постройте две точки А и В, прямую АВ А В Сколько прямых проходит через две различные точки? Постройте точку М, принадлежащую прямой АВ. МєАВ М Вопрос : Много ли точек имеет прямая?

Свойства прямой Вопрос: Как далеко уходит прямая АВ вправо? Влево? Замкнута ли прямая? А В Встретятся ли близнецы?

Отрезок Постройте прямую АВ и точки М и К, М АВ, К АВ М К Если объединить две точки прямой и все точки между ними, то получим отрезок. Отрезок МК. Измерьте длину отрезка МК : МК=

Решение задач Задача № 5 a Проведите прямую а и отметьте на ней точки А и В. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки P и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.

Решение задач Задача № 7 А) отрезки АС, ВС, СD, BD, AD. Б) отрезок CD. На рисунке изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки : а) на которых лежит точка С. Б) на которых не лежит точка В.

Луч Постройте прямую АВ, точку О, О АВ А О В Если точку объединить с одной из частей, на которые она разделила прямую, то получим луч. Луч ОВ. Луч ОА Точка О – начало луча

Решение задач Задача № 8 А) ВА и ВС, АС и АВ. Б) СВ. Проведите прямую, отметьте на ней точки А и В и на отрезке АВ отметьте точку С. А) Среди лучей АВ, ВС, СА, АС и ВА найдите пары совпадающих лучей. Б) назовите луч, который является продолжением луча СА.

Угол Постройте два различных луча ОА и ОВ О А В Угол – это геометрическая фигура, которая состоит из точки и двух исходящих из неё лучей. Точка О-вершина угла, а лучи ОА и ОВ-стороны. AOB или BOA сторона сторона

Развернутый угол

Какая точка лежит во внутренней области угла, а какая во внешней?

Самостоятельная работа По рисунку 1 ответьте на вопросы: 1. Запишите все отрезки. 2. Запишите все прямые. 3. Какие точки принадлежат прямой AD, а какие не принадлежат? Ответ запишите, используя математические символы и . 4. Укажите такую точку, которая принадлежит и прямой ВС и прямой АМ. Как еще можно назвать указанную точку? 5. По рисунку 2 запишите точки, принадлежащие: А) внешней области угла; Б) внутренней области угла; В) сторонам угла. О D B A E M K C P N Рисунок 2 A B D M C E Рисунок 1

Проверь себя! 1. AB, BD, AD, DC, BC, DM, AM. 2. AМ, BC. 3. A AD, D AD, M AD, B AD, E AD, C AD. 4. D, точка пересечения прямых ВС и АМ. 5. А) D, P, N Б) E, K, M В) A, B, O, C

Домашнее задание Пункты 3, 4 прочитать, выучить введенные понятия, № 6, 10, 13.