Презентация на тему: Числовые неравенства и их свойства

Числовые неравенства и их свойства. Гимназия № 19 г. Минск. Учитель математики Виктор Иванович Синявский.

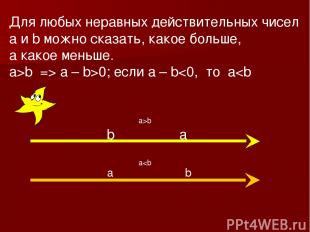
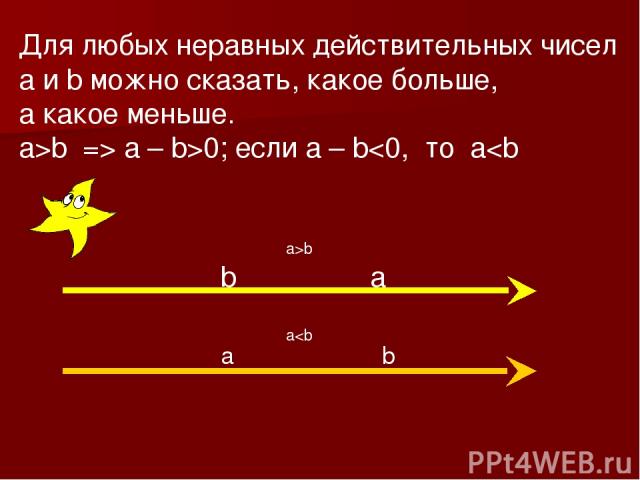
Для любых неравных действительных чисел a и b можно сказать, какое больше, а какое меньше. a>b => a – b>0; если a – b

Знаки неравенств Строгие неравенства: A>B, 67>35 d

Двойные неравенства: Двойное неравенство a < b < c верно, если одновременно верны два неравенства a < b и b < c, и неверно в противном случае. Двойное неравенство d > e > f верно, если …

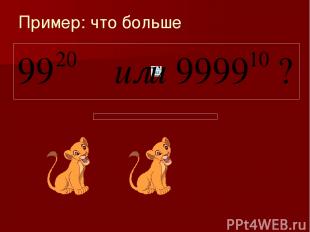
Пример: что больше

Докажите, что

Доказательство:

Свойство 1. Если aa; если а>b, то bb, то…

Свойство 2. Если a

Свойство 3. Если a

Следствие Любое число можно перенести из одной части неравенства в другую с противоположным знаком.

Свойство 4. Если a

Выводы: Если обе части верного неравенства умножить на одно и то же положительное число и сохранить знак исходного неравенства, то получится верное неравенство; Если обе части верного неравенства умножить на отрицательное число, то знак неравенства нужно поменять на противоположный.

Следствие. Если а и b – положительные числа и а

Свойство 5. Если a

Свойство 6. Если ad, то a – cd, то – с

Вывод: Два верных неравенства противоположного знака можно почленно вычитать, оставляя знак того неравенства, из которого вычитали другое неравенство.

Свойство 7 Если a,b,c,d – положительные числа, a

Итак, Если перемножить почленно два верных неравенства одного знака, левые и правые части которых положительные числа, то получится верное неравенство, имеющее тот же знак, что и данное неравенство.

Следсвия из седьмого свойства: Следствие 1. Если 0

Какие появились вопросы?

На этом мы и закончим наш сегодняшний урок