Презентация на тему: Преобразования графиков функций

Преобразования графиков функцийИсследовательская работа Выполнена ученицей 10 а классаМОУ СОШ №1 г.АрхангельскаТёмкиной Валентиной СергеевнойНаучные руководители:учитель математики ВККМОУ СОШ №1 г.АрхангельскаКотцова Ольга Валентиновнаучитель информатики и ИКТГБОУ АО Кадетская школа-интернат«Архангельский морской кадетский корпус» 2012

Актуальность: Эта тема актуальна, т.к. в конце 11 класса необходимо сдавать единый государственный экзамен по математике, куда будут включены задания, связанные с преобразованием графиков функций.Нами были проанализированы различные собрания с экзаменационными заданиями. Вывод: в сборниках КИМ единого государственного экзамена по математике встречаются задания на использование знаний о различных преобразованиях графиков функций.

Цель: Изучение способов построения графиков функций с помощью различных преобразований.Задачи:Исследовать взаимосвязь графика функции y=f(x) с графиками функций y=|f(x)|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a). Рассмотреть задания на построение графиков функций с помощью преобразований.Попробовать создать рисунок, используя исследуемые функции.Узнать, есть ли более профессиональные и эффективные системы для построения графиков в декартовых системах координат кроме Excel и Calc, которые мы использовали для построения в прошлой работе.Выявить в чём преимущества и недостатки этих компьютерных программ.

Рабочая гипотеза: графики сложных функций, можно построить с помощью преобразований графика исходной функции.Объект – графики функций.Предмет – построение графиков сложных функций с помощью преобразования графика исходной функции.Методы исследования: наблюдения, сравнения, анализ, обобщение, прогнозирование, знаковое моделирование.

Симметрия относительно оси «ох» Сохраняя ту часть, где х≥0, выполнить её симметрию относительно оси «оу» Сохраняя ту часть, где у≥0, выполнить симметрию относительно «ох» той части, где у<0

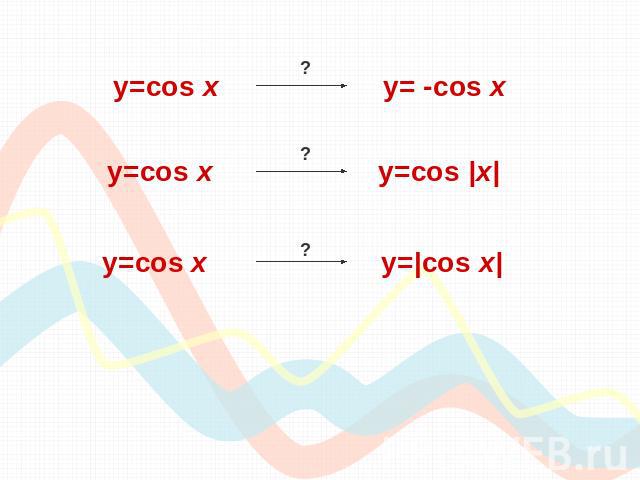
y=cos х y= -cos x y=cos х y=cos |x| y=cos х y=|cos x|

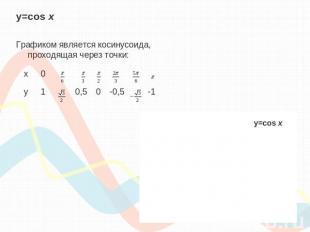
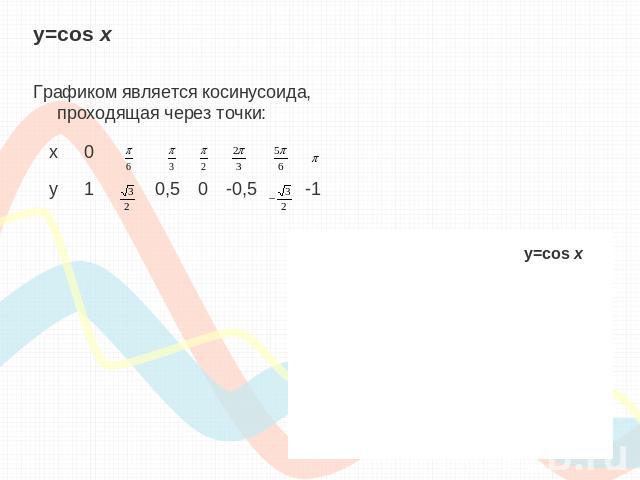
y=cos хГрафиком является косинусоида, проходящая через точки:

Для того, чтобы из графика функции y=cos x получить график функции y= - cos x , необходимо выполнить симметрию исходного графика относительно оси «ох». y=cos х y= -cos x

y=cos х y=cos |x| Для того, чтобы из графика функции y=cos x получить график функции y=cos |x|, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а это и будет сам график y=cos x.

Для того, чтобы из графика функции y=cosx получить график функции y=|cos x|, необходимо сохранить ту часть исходного графика, где у≥0, и выполнить симметрию относительно «ох» той части, где у<0.

y=cos х y=|cos |x|| Для того, чтобы из графика функции y=cosx получить график функции y=|cos|x||, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а затем сохранить ту часть получившеюся графика, где у≥0, и выполнить её симметрию относительно «ох» той части, где у<0.

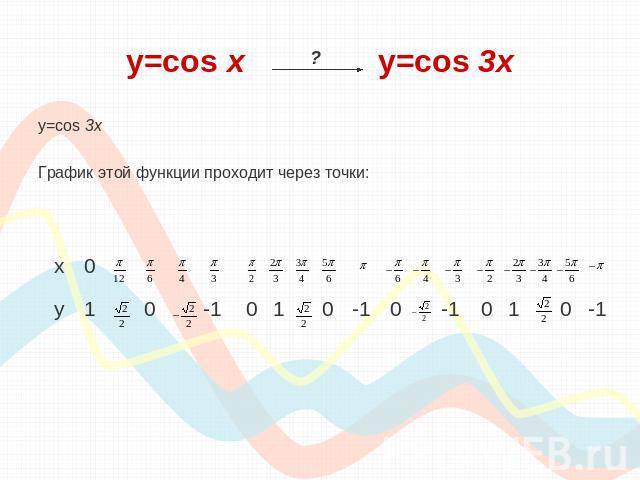
y=cos х y=cos 3x y=cos 3xГрафик этой функции проходит через точки:

y=cos х y=cos 3x Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos 3x, необходимо сжать исходный график в 3 раза вдоль «ох».

y=cos х y=cos x/3 y=cos x/3График этой функции проходит через точки:

y=cos х y=cos x/3 Вывод: Для того, чтобы из графика функции y=cos x получить график функции y=cos x/3, необходимо выполнить растяжение исходного графика в 3 раза вдоль оси «ох».

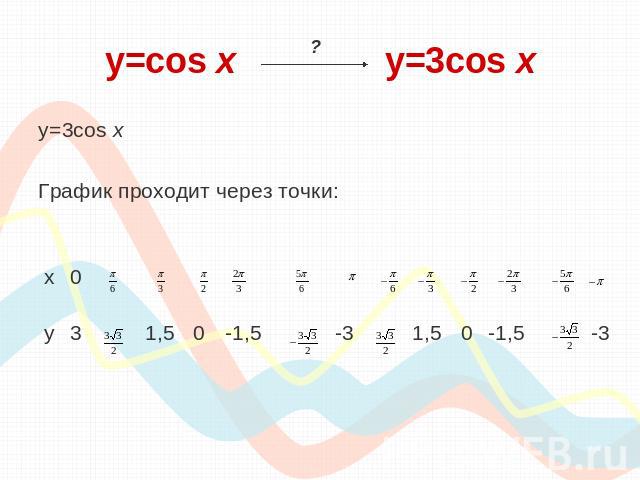
y=cos х y=3cos x y=3cos xГрафик проходит через точки:

y=cos х y=3cos x Вывод: Для того, чтобы из графика функции y=cos x получить график функции y=3cos x, необходимо растянуть исходный график в 3 раза вдоль оси «оу».

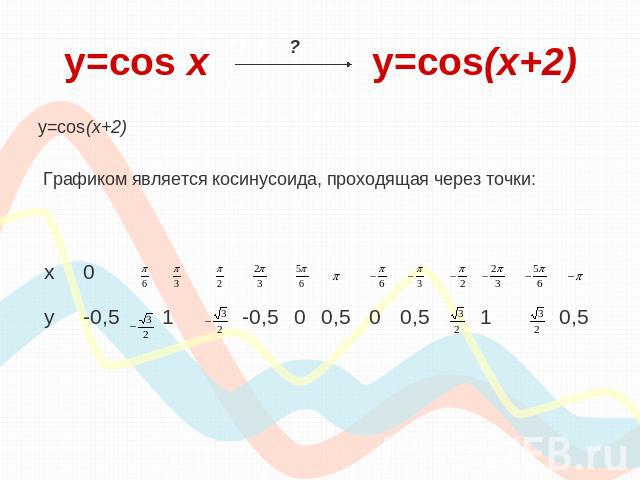
y=cos х y=cos(x+2) y=cos(x+2) Графиком является косинусоида, проходящая через точки:

y=cos х y=cos(x+2) Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos(x+2) , необходимо сдвинуть исходный график вдоль оси «ох» на 2 единицы влево.

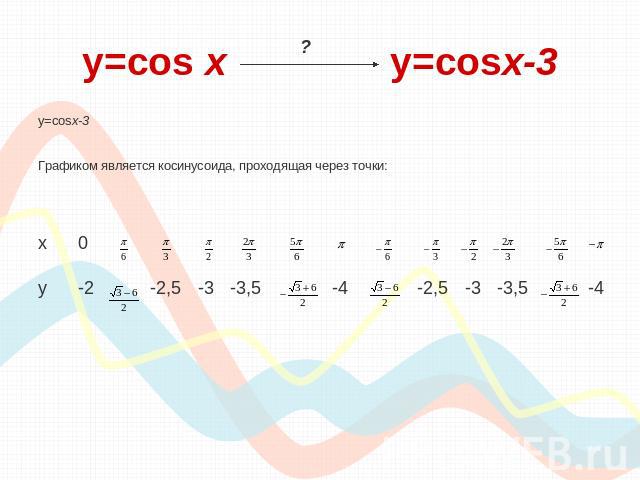
y=cos х y=cosx-3 y=cosx-3Графиком является косинусоида, проходящая через точки:

y=cos х y=cosx-3 Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos x -3, необходимо сдвинуть исходный график вдоль оси «оу» на 3 единицы вниз.

Итог: Сохраняя ту часть исходного графика, где х≥0, выполнить её симметрию относительно оси «оу» Сохраняя ту часть, где у≥0, выполнить симметрию относительно оси «ох» той части, где у<0 Если k>1, то сжатие исходного графика в k раз вдоль оси «ох», если 0<k<1, то растяжение графика в k раз вдоль «ох» Если k>1, то растяжение исходного графика в k раз вдоль оси «оу», если 0<k<1, то сжатие графика в k раз вдоль «оу» Сдвиг вдоль оси «ох», если а≥0, то на а единиц вправо, если а<0, то на а единиц влево Сдвиг вдоль оси «оу», если b≥0, то на b единиц вверх, если b<0, то на b единиц вниз

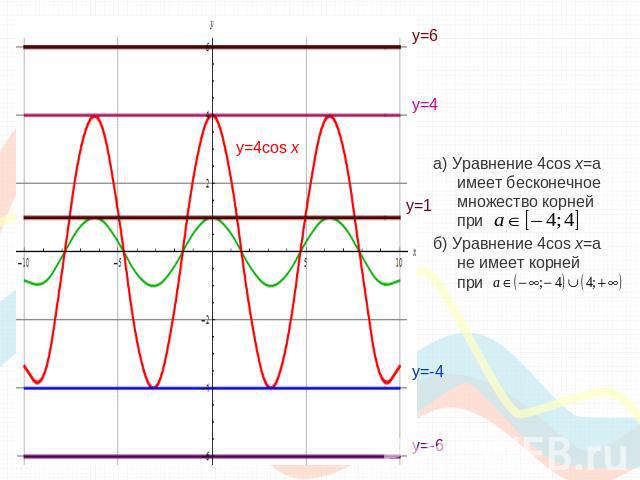
Исследование количества корней уравнения: Мы знаем, что для того, чтобы из графика функции получить график функции необходимо растянуть исходный график в 4 раза вдоль оси «оу». 2. у=а – линейная функция.Графиком является прямая, параллельная оси «ох» и проходящая через точки (2;а) и (0;а).

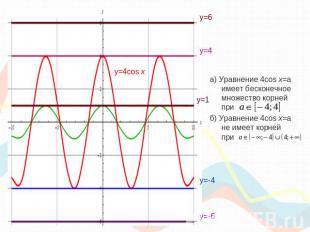
а) Уравнение 4cos x=a имеет бесконечное множество корней приб) Уравнение 4cos x=a не имеет корней при

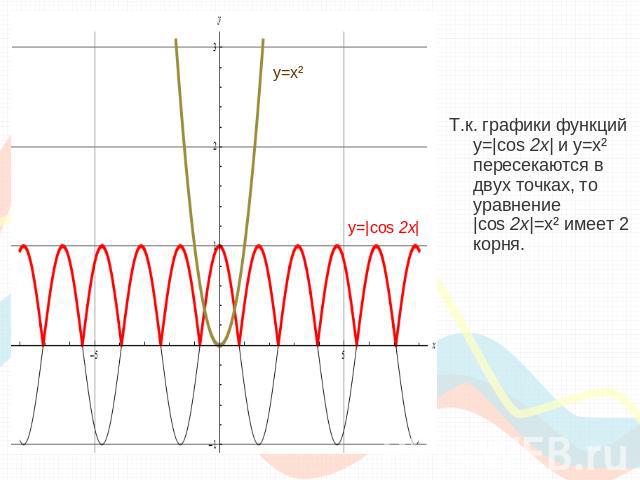
Исследование количества корней уравнения:|cos 2x|=x²y=|cos 2x|y=cos x y=cos 2x y=|cos 2x|Мы знаем, что для того, чтобы из графика функции y=cos x получить график функции y=cos 2x, необходимо сжать исходный график в 2 раза вдоль оси «ох», а затем, чтобы получить график функции y=|cos 2x|, необходимо сохранить ту часть графика, где у≥0, и выполнить симметрию относительно оси «ох» той части, где у<0.y=cos xГрафиком является косинусоида, проходящая через точки:y=x² - квадратичная функция.Графиком является парабола, ветви которой направлены вверх.(0;0) – вершина параболы.«оу» - ось симметрии параболы.

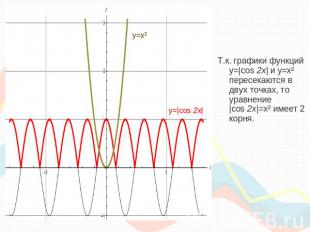
Т.к. графики функций y=|cos 2x| и y=x² пересекаются в двух точках, то уравнение |cos 2x|=x² имеет 2 корня.

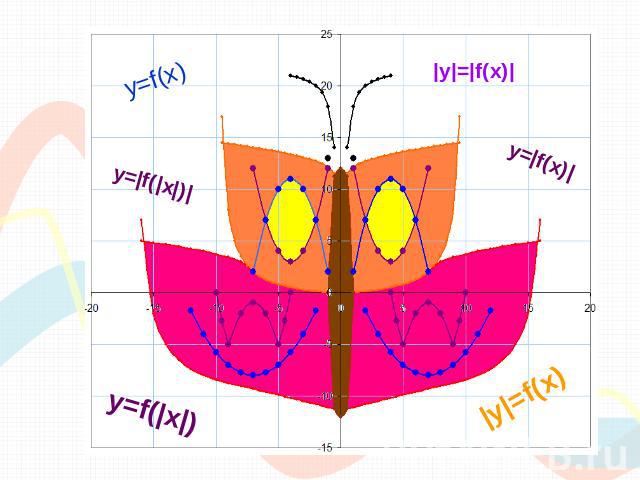
Функции, использованные для построения рисунка

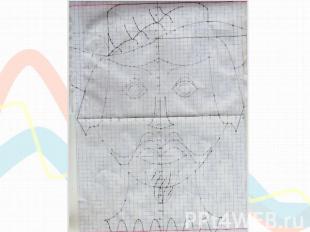
Заключение Цель достигнута, мы изучили способы построения графиков функций с помощью различных преобразований.Задачи выполнены, мы исследовали взаимосвязь графика функции y=f(x) с графиками функций y=|f(x)|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a),научились строить эти графики, рассмотрели задания с применением таких функций, построили лицо мушкетёра, используя исследуемые функции, выяснили с помощью каких программных средств кроме Excel и Calc можно строить графики функций, выявили, в чём их преимущества и недостатки. Теперь мы знаем, что для построения графиков используется не только Microsoft Office Excel и Open Office Calc, но есть и другие программы, не только не уступающие по возможностям этим программам, но и превышающие их, например,Wolfram Mathematica.

Значимость полученных результатов: сейчас нам стало известно, как строить графики сложных функций с помощью преобразований графика исходной функции, и если встретятся задания с применением этих функций, то мы будем знать, как они выполняются.Использовать эти результаты можно при решении заданий единого государственного экзамена.

Спасибо за внимание!