Презентация на тему: Построение графика неявно заданной функции на примере лемнискаты Бернулли

Тема: «Построение графика неявно заданной функции на примере лемнискаты Бернулли» Проект Гузь Ольги

Содержание. 1.Определение функции заданной неявно.2.Определение лемнискаты.3.Вывод уравнения лемнискаты.4.Преобразование уравнения лемнискаты.5.Уравнение лемнискаты в полярной системе координат.6.Исследование уравнения лемнискаты.7.Построение лемнискаты.8. Применение лемнискаты.9.Краткая историческая справка.

Определение неявно заданной функции Рассмотрим функцию, заданную неявно уравнением F(x ,y)=0.В зависимости от того, какой является функция F(x ,y)-алгебраической или трансцендентной,- кривые также делятся на алгебраические и трансцендентные.Примеры, лемниската Бернулли.
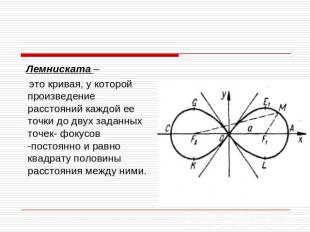
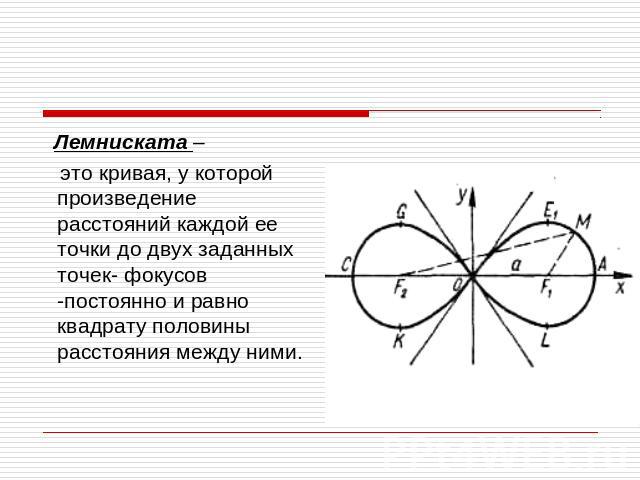
Лемниската – это кривая, у которой произведение расстояний каждой ее точки до двух заданных точек- фокусов -постоянно и равно квадрату половины расстояния между ними.

Вывод уравнения лемнискаты Пусть фокусы имеют координаты: F1(-a;0) и F2 (а;0); М(х, у) - произвольная точка геометрического места, то по условиюПодставляя в это равенство выражения получим искомое уравнение данного геометрического места

Дальнейшая цель- получить уравнение лемнискаты Бернулли в более простом виде. Возводя в квадрат обе части уравнения и группируя члены, находимотсюда

Преобразуя последнее уравнение, имеем:или в окончательном видеМы получили уравнение лемнискаты в декартовой системе координат.

Т.к х и у входят в это уравнение только в чётных степенях, то лемниската симметрична относительно координатных осей.Построить график данной функции затруднительно. Запишем это же уравнение в полярной системе координат.

Поскольку х =ρ cos φ, у = ρ sinφ, х2+у2= ρ2, то уравнение лемнискаты в полярных координатах примет видρ 4=2а2 ρ(cos2φ- sin2φ)илиρ 2=2а2 cos2φ.

Исследование уравнения лемнискаты ρ 2=2а2 cos2φИз этого уравнения видно, чтопри φ=0. Если φ увеличивается в пределах от 0 до , то ρ уменьшается от до ρ=0.Если , то ρ принимает мнимые значения. Это означает, что на лемнискате нет точек, для которых φ меняется в указанных пределах.

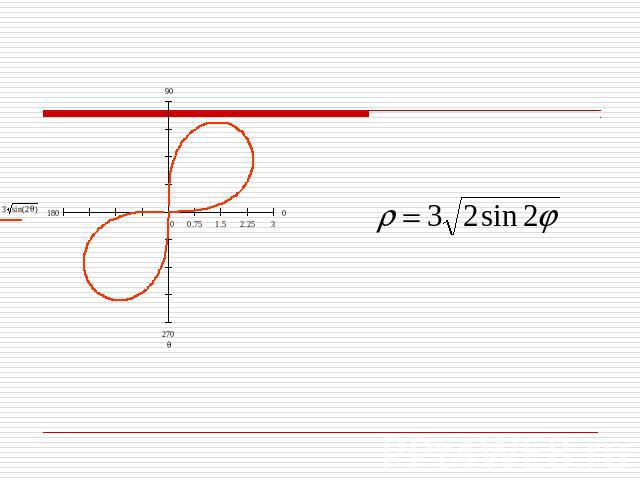
Построение лемнискаты Построим график функции при разных значениях а: при а=1
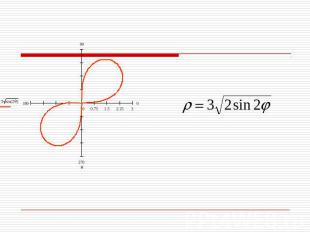
Построение лемнискаты
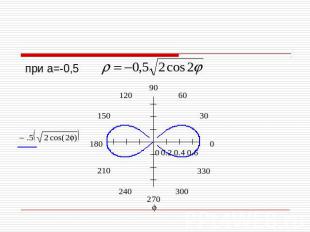
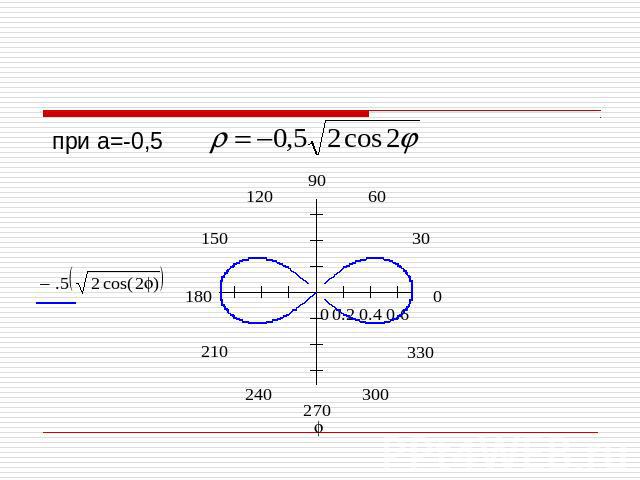
Построение лемнискаты при а=-0,5

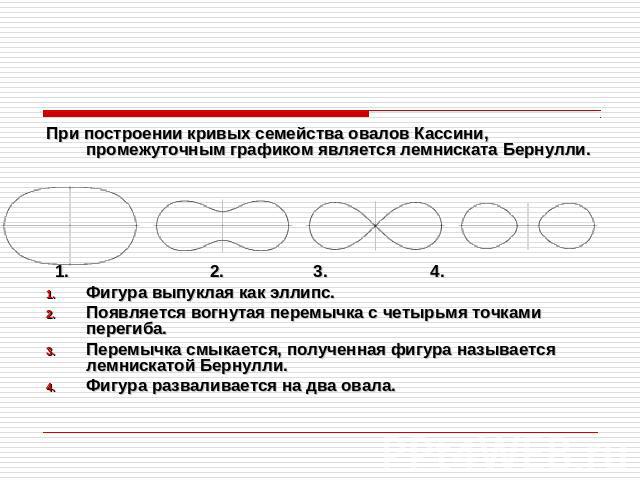
Построение При построении кривых семейства овалов Кассини, промежуточным графиком является лемниската Бернулли. 1. 2. 3. 4.Фигура выпуклая как эллипс.Появляется вогнутая перемычка с четырьмя точками перегиба.Перемычка смыкается, полученная фигура называется лемнискатой Бернулли. Фигура разваливается на два овала.

Применение: В технике лемниската применяется, в частности, в качестве переходной кривой на закруглениях малого радиуса, как это имеет место на железнодорожных линиях в горной местности и на трамвайных путях.

Способы построения лемнискаты Существует два способа построения лемнискаты. Первый способ - с помощью двух угольников и нарисованной на листе бумаги окружности (рис.2).Вершина острого угла одного из угольников находится в центре окружности, вершина прямого угла другого -на окружности.

Второй способ - с помощью шарнирного устройства, две точки которого закреплены на плоскости (рис.3).

Лемниската Бернулли.Ее автор – швейцарский математик Якоб Бернулли. Он дал этой кривой поэтическое название «лемниската». В античном Риме так называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх.
БЕРНУЛЛИ Якоб I (1654-1705). Швейцарский математик. Работал в Базельском университете.Работы посвящены математическому анализу, теории вероятностей и механике. В 1687 познакомился с первым мемуаром Лейбница по дифференциальному исчислению и применил его идеи к изучению ряда кривых, встречающихся в математике, механике, и выводу формулы радиуса кривизны плоской кривой. Ввел термин «интеграл».

Список использованной литературы ♣ Вирченко Н.А. и др.Справочник «Графики функций»; Киев: Наук. думка, 1979г;♣ И.И.Валуцэ «Математика для техникумов»; Москва, Издательство «Наука», 1980г;♣ Маркушевич А.И. «Замечательные кривые»; Москва 1978 г.

Список использованной литературы Internet-ресурсы: WWW.Colledg.Ru;WWW.5ballov.Ru; WWW.bankreferatov.Ru; WWW.rubricon.com. Программное обеспечение: MS Word; MS Power Point;Windows Media; Nero Wave Editor; Сканер.