Презентация на тему: Подструктуры математического мышления: как их выявить и использовать в преподавании

«Подструктуры математического мышления: как их выявить и использовать в преподавании»

Актуальность Математика – царица наук, пожалуй, самая точная и въедливая наука из всех. Ученые-психологи пришли к интересному выводу. В общей структуре мышления можно выделить пять типов математического мышления. Доминирующий тип и определяет мыслительную деятельность человека в разных практических случаях. Для адаптации человека в обществе и полноценного функционирования в нем необходим высокий уровень общего развития. Математическое образование вносит свой вклад в формирование общей культуры человека. Одной из основных целей обучения математике является развитие мышления учащихся. Данная работа открывает перед учащимися и учителями возможность оценить важность выявления доминирующей структуры мышления учеников, для развития индивидуальных способностей, подбора правильного курса обучения и помощи с освоением такой сложной, но интересной науки, как математика.

Определение и характеристика основных типов мышления, а также выявление доминирующих структур математического мышления на базе 5-х и 11-х классов, дляпомощи учителям в построение процесса обучения с учетом математической индивидуальности учеников. Дать определения и охарактеризовать основные подструктуры мышления Показать важность выбора учителем правильного курса обучения математике Выявить доминирующие структуры математического мышления школьников младшего и старшего звена

Каждый выдающийся математик отличался собственным стилем творчества, проявлявшимся во многих произведениях. Историческая справка Для Архимеда - гениальный своей простотой и смелостью механико-геометрический стиль доказательств Для Демокрита был характерен математический атомизм, ставший первым предвестником дифференциального и интегрального исчислений.

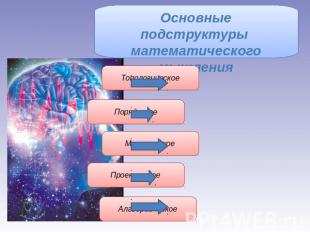
Основные подструктуры математического мышления

Топологическое мышление Задачу сто раз «проверят», ошибок не допускают

Порядковое мышление Задачу решают строго по алгоритму «Порядковцы» любят строгий линейный порядок В любых действиях стараются выработать алгоритм, зависящий от какого-то объективного принципа.

Алгебраическое мышление Задачу решают быстро без объяснений, часто ошибаются Алгебраистов сложно заставить делать что-то по правилам К решению каких-либо задач подходят с хаотическим настроем – начинают с того места, которое им нравится

Метрическое мышление Задачу решают по действиям Они всегда ясно представляют себе, что выйдет в результате работы

Проективное мышление Задачу решают самым неожиданным способом Самый сложный тип из всех пяти «Проективисты» склоны рассматривать предмет с разных точек зрения Мыслят нестандартно, удивляют окружающих многовариантностью решений

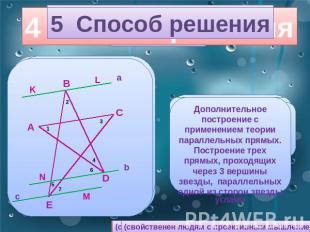
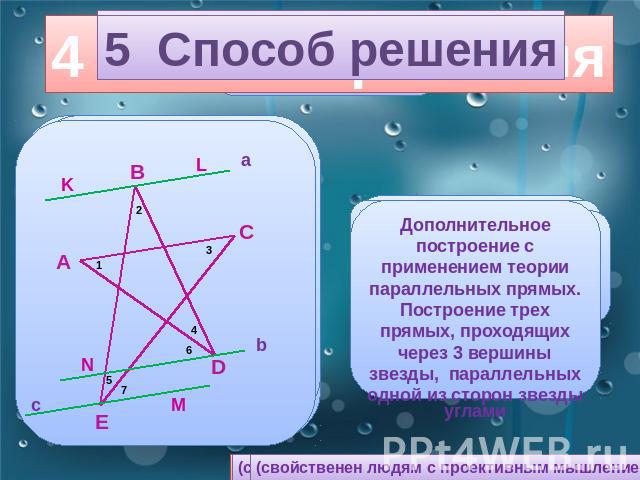
5 Способ решения Дополнительное построение с применением теории параллельных прямых.Построение трех прямых, проходящих через 3 вершины звезды, параллельных одной из сторон звезды

Исследование на базе 2х и 5х классов

Исследование на базе 9-11 классов

Результирующая диаграмма Всего анкетируемых – 204 человек

Наши рекомендации Проводить входящее тестирование (1й класс; 5й класс;). Чем раньше учитель узнает тип мышления ученика, тем проще потом будет строить процесс обучения, и благодаря этому, ребенку в будущем будет легче раскрыть свои способности, и он сможет легче усваивать учебный материал. Не навязывать детям тот способ рассуждения, который свойствен самому учителю. В этом случае дети, ведущая подструктура которых совпадает с ведущей подструктурой педагога, легко его понимают, для них он понятно и доступно объясняет. Для остальных же школьников усвоение математики становится мукой.

Наши рекомендации Зная математические особенности учеников, учитель может учитывать их при составлении учебного плана, а также подбирать задачи с несколькими вариантами решения. Проводить выходящие тесты (9й класс; 11й класс). Этот вид тестирования сможет помочь выпускникам подобрать правильный курс при подготовке к предстоящим экзаменам, а также, возможно, поможет определиться с выбором будущей профессии. Не ломать математическую индивидуальность ученика, а учитывать ее и строить процесс обучения в соответствии с ней – главная задача.

Заключение В результате проделанной нами работы, мы добились реализации поставленных перед собой целей. Во-первых, подробно изучили основные типы мышления. Во-вторых, показали важность выявления доминирующей структуры мышления учеников. В-третьих, показали важность выбора учителем правильного курса обучения математике. В-четвертых, проведя собственное исследование, выявили доминирующие структуры математического мышления школьников младшего и старшего звена.

Спасибо за внимание!

Список использованной литературы:Каплунрович И.Я. Пять подструктур математического мышления// «Математика в школе» [Текст] // И.Я. Каплунрович, Т.А. Петухова//1998. – №5. – с.45Баженова И.Н. Педагогический поиск [Текст]//Сост. И.Н. Баженова. – М.: Изд. П24 Педагогика,1987. – 544с.Возрастная психология: Учебное пособие для студентов вузов. — М.: Академический Проект- Екатеринбург: Деловая книга, 2000. — 624 с.Дорофеев Г.В. «Математика в школе» [Текст]//Дорофеев Г.В.//2007. – №3. – С.17 Зинченко В.П. Большой психологический словарь [Текст]//Сост. и общ. ред. Б.Г.Мещеряков, В.П.Зинченко. – СПб.: Изд. Прайм-ЕВРОЗНАК, 2007.-672с. Иванов П.И. «Общая психология» [Текст]// (Переработ. и доп. изд.) Ташкент.- 1967. Корзникова Г.Г. Обучение интеллектуально одаренных старшеклассников: содержание умений и навыков самообразования: Метод. Рекомендаций [Текст] //Урал. Гос. пед. ун-т. - Екатеринбург,2004.-29с.Немов. Р.С. Психология. Учеб. для студентов высш. пед. учеб. Заведений [Текст] В 3 кн. Кн. 2. Психология образования/ Р. Немов.— М.: Изд. «Просвещение»: ВЛАДОС, 1995. - 496 сПетровский А.В. Введение в психологию [Текст]/ / Под общ. ред. проф. А. В. Петровского. – М.: Издательский центр "Академия", 1997.- 496с.Фридман Л.М. Психологическая наука – учителю [Текст]// Л.М. Фридман, К.Н. Волков. – М.: Изд. «Просвещение», 1985. – 224с. Фридман Л.М. Теоретические основы методики обучения математике: Пособие для учителей, методистов и педагогических высших учебных заведений.[Текст]// М. Московский социальный институт: Флинта 1998.Шумилин Е.А. Психологические особенности личности школьников [Текст]//Под. ред. В.В.Давыдова. – М.: Изд. Педагогика, 1979. – 152с.