Презентация на тему: По следам теоремы Пифагора

По следам теоремы Пифагора Работа выполнена ученицей 9 класса МОУ СОШ №19 ст.Ладожской Усть-Лабинского района Селезнёвой Дарьей Андреевной Руководитель: Огнева Раиса Стефановна, учитель математики МОУ СОШ №19, Заслуженный учитель Кубани, Заслуженный учитель России, победитель конкурса «Лучший учитель России» в рамках реализации ПНПО.

« Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, которую можно сравнить с мерой золота…» И. Кеплер

Цель: внимательно изучив формулировку теоремы Пифагора, проанализировав доказательство и используя обобщение, предложить более широкий круг объектов, при помощи которых происходит доказательство теоремы Пифагора, создав тем самым новую интерпретацию её формулировки.Задачи: 1) обобщение материала по исследуемой теме. 2) применение теоремы Паппа как дополнительного инструмента проекта. 3) систематизирование информации, представленной в проекте. 4) создание новой интерпретации формулировки теоремы Пифагора.

ГИПОТЕЗА Если я (в доказательстве теоремы Пифагора) на сторонах прямоугольного треугольника построю не квадраты (как предложил Пифагор), а подобные многоугольники, то будет ли справедливо, что площадь многоугольника, построенного на гипотенузе, равна сумме площадей многоугольников, построенных на катетах? Если я это докажу, то у меня появится новая интерпретация формулировки теоремы Пифагора, что обогатит задачный материал, а главное, будет иметь интересное обобщение.

Теорема Паппа Если на сторонах произвольного треугольника АВС построить параллелограммы соответствующим образом, то площадь параллелограмма, построенного на большей стороне, равна сумме площадей двух остальных.

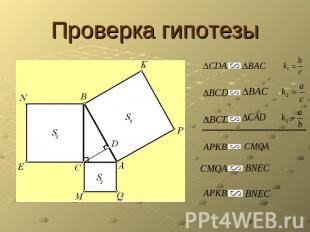
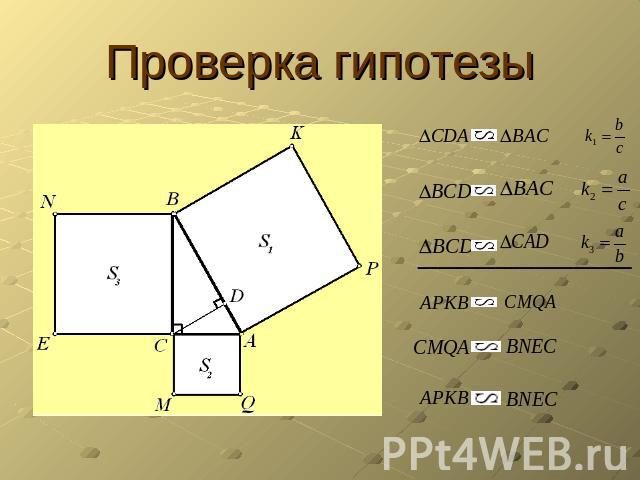
Проверка гипотезы

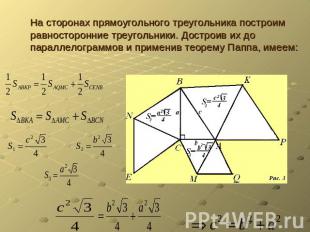
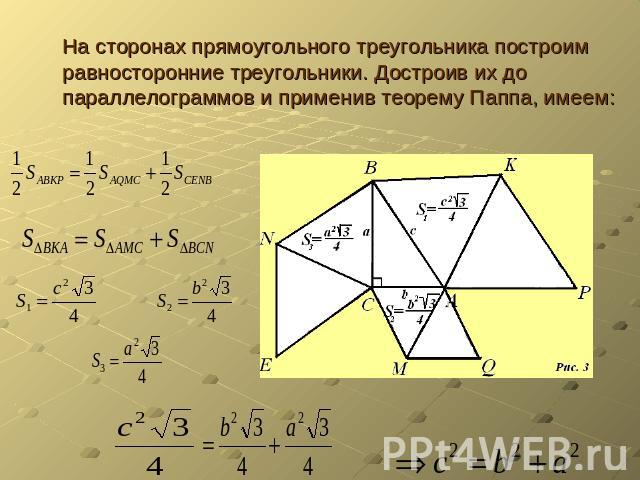
На сторонах прямоугольного треугольника построим равносторонние треугольники. Достроив их до параллелограммов и применив теорему Паппа, имеем:

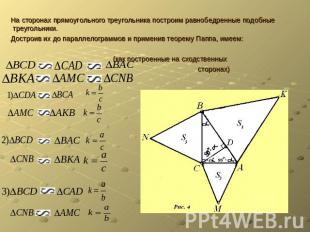
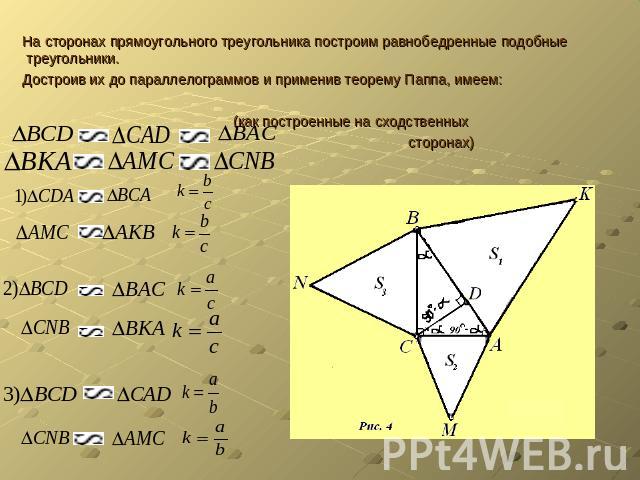
На сторонах прямоугольного треугольника построим равнобедренные подобные треугольники. Достроив их до параллелограммов и применив теорему Паппа, имеем: (как построенные на сходственных сторонах)

На сторонах прямоугольного треугольника построим разносторонние подобные треугольники с коэффициентами подобия соответственно (это коэффициенты подобных треугольников, на которые делит высота, опущенная из вершины прямого угла треугольника).Достроив их до параллелограммов и применив теорему Паппа, получим, что площадь треугольника, построенного на гипотенузе, равна сумме площадей треугольников, построенных на катетах. SABKP = SAQMC + SBCEN SABKP= SAQMC + SBCEN S1 = S2 + S3

Новая интерпретация формулировки теоремы Пифагора Если на сторонах прямоугольного треугольника, как на сходственных, построить подобные многоугольники, то площадь многоугольника, построенного на гипотенузе, равна сумме площадей многоугольников, построенных на катетах.