Презентация на тему: Теорема Пифагора. И её доказательства

Теорема Пифагора.И её доказательства.

"Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах." Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например, для ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.

Древнекитайское доказательство Древнеиндийское доказательство Это интересно… Биография Пифагора Последний слайд Доказательство теоремы Пифагора «Золотые Стихи» Пифагора

Древнекитайское доказательство. Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла тематика в девяти книгах» — главное из сохранившихся математико - астрономических сочинений в книге «Математики» помещен чертеж (рис. 2, а), доказывающий теорему Пифагора. Ключ к этому доказательству Рис. 2 подобрать нетрудно.

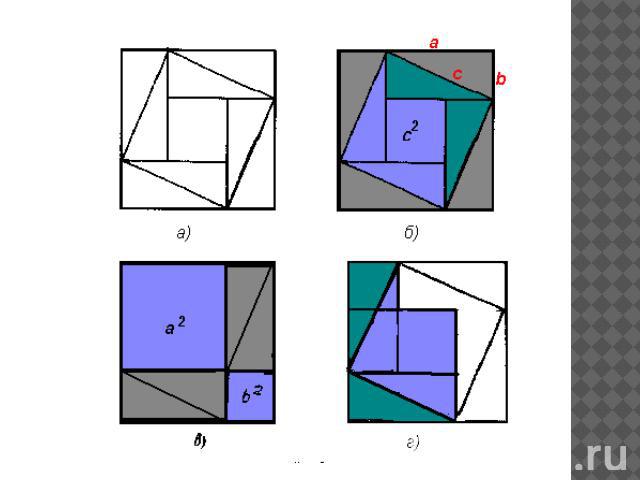
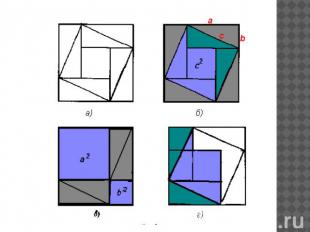
В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний — квадрат со стороной с, построенный на гипотенузе (рис. 2, б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. 2, в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис. 2, а), не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (рис. 2, б) отрезать и приложить гипотенузами к двум другим гипотенузам (рис. 2, г), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b, т.е. с2=а2+Ь2.

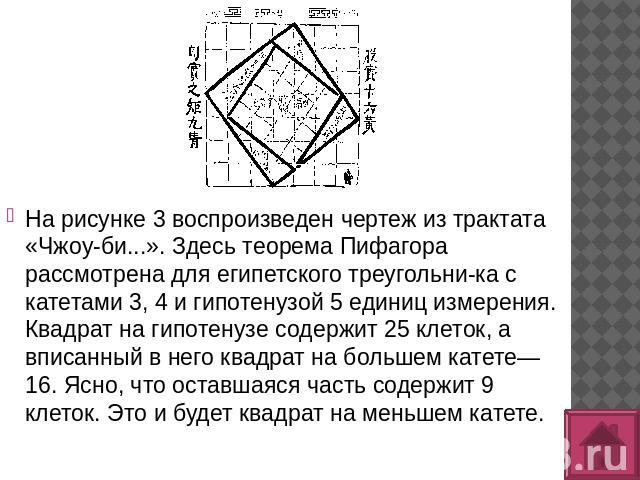
На рисунке 3 воспроизведен чертеж из трактата «Чжоу-би...». Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете—16. Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете.

Древнеиндийское доказательство. Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж (рис. 4, а) с характерным для индийских доказательств словом «смотри!». Как видим, прямо-угольньные треугольники уложены здесь гипотенузой наружу и квадрат с2 перекладывается в «кресло невесты» а2-b2 (рис. 4, б). Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше площади данного квадрата) встречаются в древнеиндийском трактате «Сульва сутра» (VII —V вв. до н.э.).

Еще давно была изобретена головоломка, называемая «Пифагор». Нетрудно убедиться в том, что в основе семи частей головоломки лежат равнобедренный прямоугольный треугольник и квадраты, построенные на его катетах, или, иначе, фигуры, составленные из 16 одинаковых равнобедренных прямоугольных треугольников и потому укладывающиеся в квадрат. Такова лишь малая толика богатств, скрытых в жемчужине античной математики — теореме Пифагора. Далее я рассмотрю несколько алгебраических доказательств теоремы.

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА. Пусть Т— прямоугольный треугольник с катетами а, b и гипотенузой с (рис. 6, а). Докажем, что с2=а2+Ь2.Построим квадрат Q со стороной а+Ь (рис. 6, б). На сторонах квадрата Q возьмем точки А, В, С, D так, чтобы отрезки АВ, ВС, CD, DA отсекали от квадрата Q прямоугольные треугольники Т1, Т2, Т3, Т4 с катетами а и b. Четырехугольник ABCD обозначим буквой Р. Покажем, что Р — квадрат со стороной с.Все треугольники Т1, Т2, Т3, Т4 равны треугольнику Т (по двум катетам). Поэтому их гипотенузы равны гипотенузе треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырехугольника прямые.

Пусть и — величины острых углов треугольника Т. Тогда, как вам известно, += 90°. Угол у при вершине А четырехугольника Р вместе с углами, равными и , составляет развернутый угол. Поэтому +=180°. И так как += 90°, то =90°. Точно так же доказывается, что и остальные углы четырехугольника Р прямые. Следовательно, четырехугольник Р — квадрат со стороной с.Квадрат Q со стороной а+Ь слагается из квадрата Р со стороной с и четырех треугольников, равных треугольнику Т. Поэтому для их площадей выполняется равенство S(Q)=S(P)+4S(T) .Так как S(Q)=(a+b) 2 ; S(P)=c2 и S(T)=1/2(ab), то, подставляя эти выражения в S(Q)=S(P)+4S(T), получаем равенство(a+b) 2=c2+4*(1/2)ab . Поскольку (a+b)2=a2+b2+2ab, то равенство (a+b)2=c2+4*(1/2)ab можно записать так: a2+b2+2ab=c2+2ab.Из равенства a2+b2+2ab=c2+2ab следует, что с2=а2+Ь2.Ч.Т.Д.

ЕЩЕ ОДНО АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО.Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 7).По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) соsА=AD/AC=AC/AB. Отсюда AB*AD=AC2. Аналогично соsВ=BD/BC=BC/AB. Отсюда AB*BD=ВС2. Складывая полученные равенства почленно и замечая, что AD+DB=AB, получим:АС2+ВС2=АВ(AD + DB)=АВ2. Теорема доказана.

В заключении еще раз хочется сказать о важности теоремы. Значение ее состоит прежде всего в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. К сожалению, невозможно здесь привести все или даже самые красивые доказательства теоремы, однако хочется надеется, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней.

«Золотые стихи» содержат в себе ту часть эзотерического учения Пифагора, которую он и его последователи признали возможным открыть непосвященным. Лизий, его ученик, после разгрома чернью пифагорейских общин в Великой Греции, принес эти стихи с собою в Элладу, где завещал своим единомышленникам читать их ежедневно утром и вечером. О том, что правило это соблюдалось у пифагорейцев в течение целого ряда веков, мы знаем от Цицерона, Горация, Сенеки, Галиена и других древних писателей. Сохранились они для нас целиком в комментариях Гиероклеса и в отрывках у классиков и Отцов Церкви. Сообразно трем степеням посвящения, стихи эти разделялись на три части: «Приготовление», «Очищение» и «Совершенствование».…Перевод Е. П. Казначевой.

«ЗОЛОТЫЕ СТИХИ» ПИФАГОРА ПРИГОТОВЛЕНИЕДолжен бессмертным богам приносить ты законченную жертву;Веру свою сохранять; чтить память великих героев;Духам земным воздавать обычное им поклоненье.

ОЧИЩЕНИЕ Мать и отца уважай вместе с родными по крови.Другом себе избери истинно-мудрого мужа;Слушай советов его, следуй его ты примеру;Из-за ничтожных причин с ним никогда ты не ссорься.Если в твоей это власти, ибо закон непреложныйТесно связует возможность с необходимостью вместе.Страсти свои побороть свыше дана тебе сила,Так обуздай же в себе мощным усилием волиАлчную жадность, и лень, похоть и гнев безрассудный.Равно один и при людях, бойся дурного поступка;Больше всего же стыдиться должен ты сам пред собою.Будь справедлив и в словах, и в поступках своих неизменно,

Следуя в них непреклонно веленьям ума и закона;Помни, что рок неизбежный к смерти людей всех приводит,Помни, что блага земные, как с легкостью людям даются,Так же легко исчезают. Что же касается горя,Данного людям Судьбою, — то должен его ты с терпеньемКротким сносить, но при этом сколько возможно старатьсяГоречь его облегчать: ибо бессмертные богиМудрых людей не повергнут свыше их силы страданью.Много путей существует для хода людских рассуждений;Много меж ними дурных, много и добрых, но преждеНужно в них зорко вглядеться, чтоб выбрать из них настоящий.

Если же в мире возьмет верх заблужденье над правдой,Мудрый отходит и ждет воцарения истины снова.Слушай внимательно то, что тебе я скажу, и запомни:Да не смущают тебя поступки и мысли чужие;Да не побудят тебя к вредным словам и деяньям.Слушай советы людей, сам размышляй неустанно,Ибо безумный лишь может действовать без рассужденья;Делай лишь то, что потом в горе тебя не повергнетИ не послужит тебе причиной раскаянья злого.За неизвестное дело ты не дерзай приниматься,Но научися ему; этим ты счастья достигнешь.Но изнурять ты не должен тело свое, а старатьсяПищи, питья, упражнений в меру давать ему, дабыТело твое укрепилось, не зная излишеств и лени.В жизни своей соблюдай, сколько возможно, порядок,Роскошь во всем изгони, ибо она возбуждаетЗависть людей неизбежно. Бойся скупым быть излишне,Бойся добро расточать, как те, что не знают работы;Делай лишь то, что тебя ни теперь, ни потом не погубитИ потому обсуждай каждый свой шаг и поступок.

СОВЕРШЕНСТВОВАНИЕ Да не сомкнет тихий сон твои отягченные вежды,Раньше чем трижды не вспомнишь дневные свои ты поступки.Как беспристрастный судья их разбери, вопрошая:«Доброго что совершил я? Из должного что не исполнил?»Так проверяй по порядку все, что с утра и до ночиСделал ты в день — и за все, что содеяно было дурного,Строго себя обличай, веселясь на добро и удачу.Пользуйся сим наставленьем; думай над ним непрестанноИ постарайся к нему навсегда привязаться всем сердцем,

Ибо советы мои тебя к совершенству приблизят.В этом клянусь тебе Тем, Кто вложил в нашу душу Тетраду,Символ божественной сущности и добродетели высшей;Но принимаясь за дело, прежде к богам обратисяС жаркой молитвой, дабы с помощью их ты окончилДело свое; а когда на пути ты своем укрепишься,Все о бессмертных богах ты узнаешь, а также о людях,О разделеньи существ; о Том, Кто в Себе их содержит,Цепью единой скрепляя, а также о том, что Природа

Мира сего однородна и в Вечном мертвого нет вещества.Это познав, ты надеждой тщетной себя не обманешь, -Все тебе будет открыто.Будешь ты знать еще то, что люди свои все несчастьяСами своею виной на себя навлекают в безумьиИ выбирают свободно каждый свои испытанья.Горе несчастным! В своем ослепленьи безумном не видятЛюди, что в их глубине таится желанное счастье.Очень немного меж нами тех, что усилием могутСбросить несчастье с себя, ибо их Рок ослепляет:

Словно колеса они катятся с гор, за собоюГорестей бремя влача и раздоров, что с ними родятся,Их управляя судьбой незаметно до самой кончины.Вместо того, чтоб искать ссоры, где только возможно,Люди должны бы ее избегать, уступая без спора.Отче Зевес всемогущий! Ты один в силах избавитьРод весь людской от несчастья, Демона им показавши,Что ослепляет их очи. Все же не должен надеждуТы покидать на спасенье, ибо божественен кореньРода людского и тайны Природа ему открывает.

Если же в них ты проникнешь, то скоро окончить ты сможешьТо, что тебе предписал я. Так излечив свою душу,Будешь вполне ты свободен от этих работ над собою.Но воздержися от мяса, оно помешает природеПри очищеньи твоем. Если же хочешь избавитьДушу свою от земного, то руководствуйся свышеДанным тебе пониманьем. Пусть оно правит судьбою!После того как очистишь душу свою совершенно,Станешь ты богом бессмертным, смерть раздавившим стопою.

Биография Пифагора. Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора не известно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера.

Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал.

В 548 г. до н.э. Пифагор прибыл в Навкратис – самосскую колонию, где было у кого найти кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была чисто прикладной наукой (удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу.

Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучится. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат.

Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принцыпов достойны подражания и сейчас.

...Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством. 

Сделала презентацию:Ученица 8 класса АМОУ гимназии школы №9У Валерия.