Презентация на тему: Теорема Пифагора и способы её доказательства

Управление образования администрации городского округа город Волжский Волгоградской области Муниципальное образовательное учреждениесредняя общеобразовательная школа №14 «Зелёный шум» «Теорема Пифагора и способы её доказательства» Автор:Тагаева К.И. Руководитель: Лопатина И.С.

Cуть истины вся в том, что нам она – навечно,Когда хоть раз в прозрении её увидим свет,И теорема Пифагора через столько летДля нас, как для него, бесспорно безупречна… Шамиссо

«Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора…» «Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора…»

Цель:Рассмотреть классические и малоизвестные доказательства теоремы Пифагора Познакомиться с областями применения теоремы и с фактами истории открытия теоремы ПифагораСделать выводы о значимости теоремы Пифагора

Пифагор Самосский (570-500 гг. до н.э.)

Некоторые факты из жизни Пифагора:Родился на о.Самосе около 570 г. до н.э. Учился во многих городах мира у великих учёных- Ферекида, Фалеса, Гермодаманта… В Египте Пифагор попал в персидский плен,где пробыл 12 летВ Кротоне(Италия) учредил «Пифагорейскую школу»

РАЗЛИЧНЫЕ СПОСОБЫ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ПИФАГОРА

Формулировка теоремы Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

ДОКАЗАТЕЛЬСТВО, основанное на равновеликости фигур: «Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах».

Алгебраический метод доказательства теоремы: Пусть F- прямоугольный треугольник со сторонами a,b и c,а Q- квадрат со стороной с. SABCD= 4S▲ + SQ= = 4·1/2 ab +c2 == 2 ab + c2 SABCD= (а+b)2 = a2 + 2ab +b2 2 ab + c2 =a2 + 2ab +b2 => c2 = a 2 +b 2

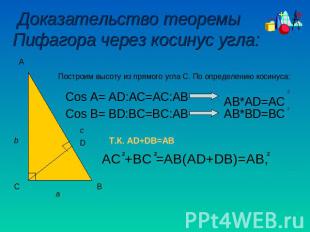
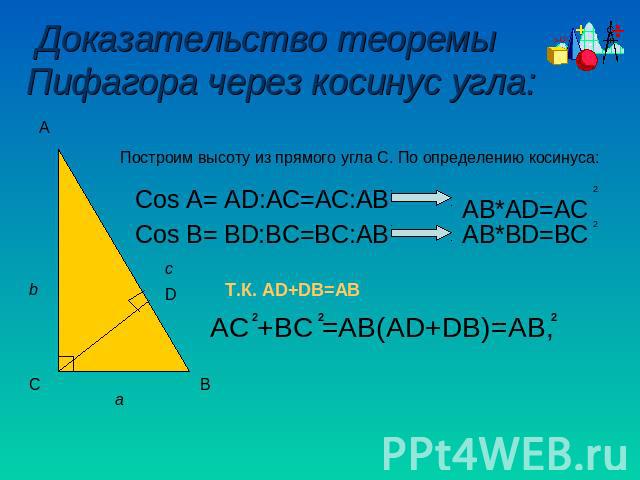
Доказательство теоремы Пифагора через косинус угла: Построим высоту из прямого угла С. По определению косинуса: Cos A= AD:AC=AC:AB Сos B= BD:BC=BC:AB AB*BD=BC

Векторное доказательство теоремы: АВС - прямоугольный треугольник, построенный на векторах. b+c=a c = a - bc²=a²+b²-2abТ.к. a b, то ab=0, c²=a²+b² или c²=a²+b²

Доказательство Гарфилда: ABC-прямоугольный треугольник 1)CD =AВ; ED=АС; ЕD AD2) SABED=2*AB*AC/2+BC/ 2 3) SABED=(DE+AB)*AD/2. 4) AB*AC+BC /2=(DE+AB)(CD+AC)/2AB*AC+BC /2= (AC+AB) /2AB*AC+BC/2= AC/2+AB/2+AB*ACBC=AB+AC

ДОКАЗАТЕЛЬСТВО БХАСКАРИ-АЧАРНА: Пусть катеты прямоугольных ▲-ков d равны a и b, а гипотенуза – с. Тогда (a − b) +(4ab)/2= с, то есть

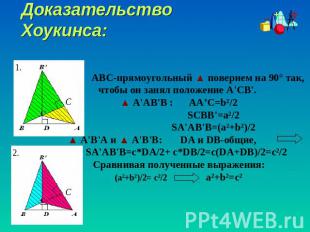
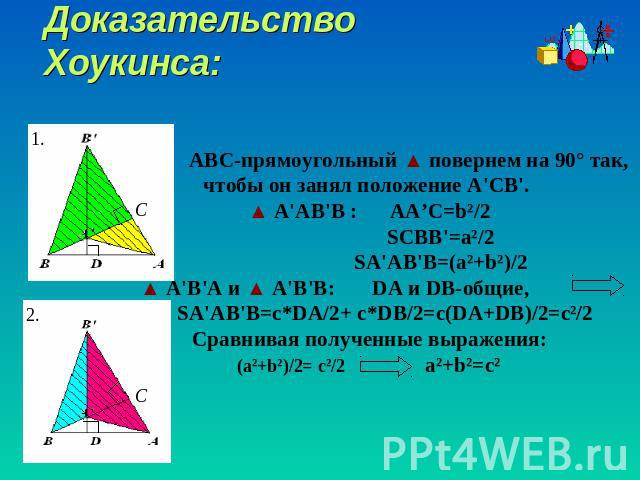
Доказательство Хоукинса: ABC-прямоугольный ▲ повернем на 90° так, чтобы он занял положение A'CB'. ▲ A'АВ'В : AA’C=b²/2 SCBB'=a²/2 SA'AB'B=(a²+b²)/2 ▲ A'В'А и ▲ A'В'В: DA и DB-общие, SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2Сравнивая полученные выражения:(a²+b²)/2= c²/2 a²+b²=c²

ДОКАЗАТЕЛЬСТВО ЕВКЛИДА: ABC-прямоугольный ▲; AJ- высота.Докажем: S1+S2=S31.▲ ABD= ▲ BFC (т.к. BF=AB; BC= BD; FBC равен ABD)2. S ▲ ABD=1/2 S BJLD, т.к. у ▲ ABD и BJLD общее основание BD и общая высота LD. S ▲ FBC=1/2 S ABFH (BF-общ.основание, AB-общая высота). Т.К. S ▲ ABD=S ▲ FBC, S BJLD=S ABFH. ▲ BCK=▲ ACE, S JCEL=S ACKG.S ABFH+S ACKG=S BJLD+ S JCEL=S BCED.

Области применения теоремы Пифагора архитектура вычисление длин отрезков некоторых фигур на плоскости мобильная связь астрономия литература

Знаменитый египетский треугольник 3, 4,5-одна из Пифагоровыхтроек

Теорема Пифагора- живительный источник красоты, совершенства и творчества для новых поколений!

Список использованнойлитературы А.П.Киселёв ,Геометрия. Часть первая. Планиметрия, Москва,Просвещение,1969г. Г. Глейзер,Учебно-методическая газета Математика, №4 2005г.Г.Остренкова,Учебно-методическая газета Математика, №24 2001г.Е.Е.Семёнов «Изучаем геометрию», Москва, Просвещение ,1987г.З.А.Скопец Геометрические миниатюры , Москва, Просвещение,1990г.Интернет-источники: http://bankreferatov.ru/ http://kvant.ru/ http://th-pif.narod.ru/formul.htmlМ.В.Ткачева Домашняя математика , Москва, Просвещение,1994г.