Презентация на тему: Некоторые доказательства теоремы Пифагора

Некоторые доказательства теоремы Пифагора

Краткая биографическая справкаФормулировка теоремыПростой способДоказательство ЭпштейнаДоказательство БхаскариДоказательство ГорфилдаТеорема, обратная теореме ПифагораПифагоровы треугольникиЕгипетский треугольник

ПифагорРодился около 570, умер около 500 до н.э. Древнегреческий философ и математик, основатель пифагорейской школы;Известно, что Пифагор покинул свой родной остров Самос в Эгейском море у берегов Малой Азии в знак протеста против тирании правителя. Он много путешествовал по странам Востока : был в Египте, в Вавилоне, где познакомился с восточной математикой. Пифагор впервые разделил числа на четные и нечетные, простые и составные…

Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

Простой способ

Смотри !!!

Доказательство Бхаскари

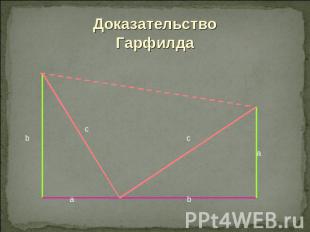
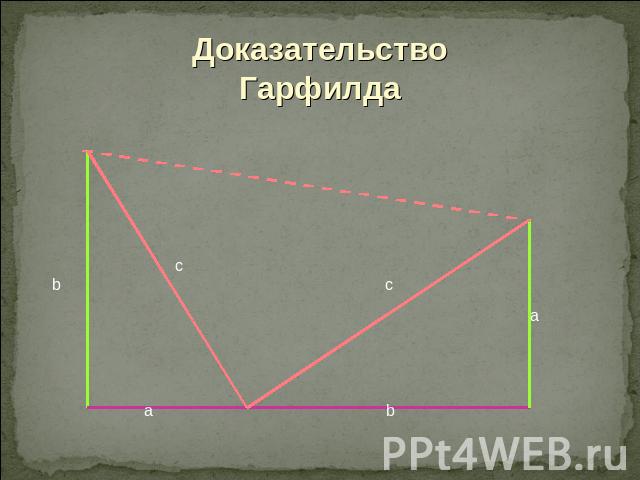
Доказательство Гарфилда

Доказательство:S трапеции = ½ (a + b) ( a + b) S треугольников = ½ a b + ½ a b + ½ с2½ (a + b) (a + b)= ½ a b + ½ a b + ½ c2

Решение1). ½ ( a2 + a b + a b + b 2) = ½ a2 + ½ a b + ½ a b + +½ b2= ½ a2 + a b + ½ b22). ½ a b + ½ a b + ½ c2 = a b + ½ c2Приравниваем 1). и 2).½ a2 + a b + ½ b2= a b + ½ c2 ½ a2 + ½ b2 = ½ c2 c2=a2 + b2

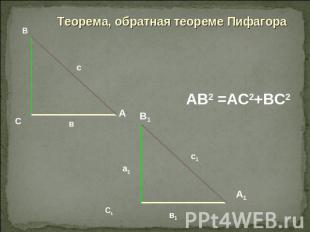
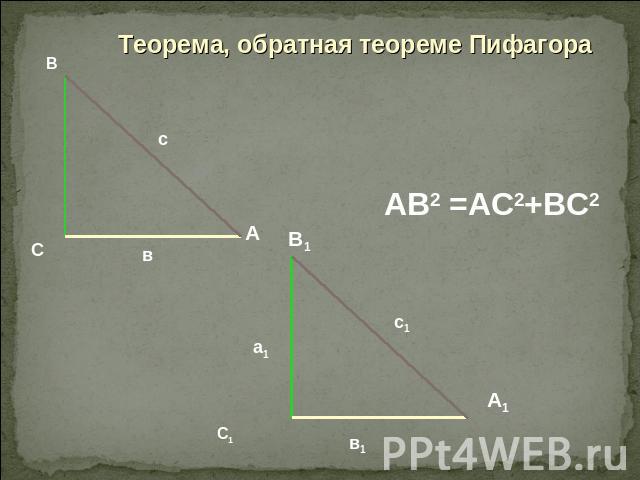
Теорема, обратная теореме Пифагора

Пифагоровы треугольникиПо теореме, обратной теореме ПИФАГОРА, треугольник со сторонами 3, 4 и 5 является прямоугольным: 25 = 16 + 9 , 25=25Прямоугольными также являются треугольники со сторонами 5, 12, 13; 8, 15, 17 и 7, 24, 25.

Египетский треугольникЭтим свойством пользовались еще древние египтяне для построения прямых углов при планировке земельных участков и сооружений зданий.

Египетский треугольникТреугольник со сторонами 3, 4 и 5 часто называют ЕГИПЕТСКИМ ТРЕУГОЛЬНИКОМ, так как он был известен еще древним египтянам. Для построения прямых углов египтяне поступали так:на веревке делали метки, делящие ее на 12 равных частей,

Египетский треугольниксвязывали ее концы и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол между сторонами, равными 3 и 4, оказывался прямым

ИсточникиБ.С.Э.Энциклопедический словарь юного математикаВ.Литцман « Теорема Пифагора»А.Немировский «Пифагор»З.А.Скопец «Геометрические миниатюры»Д.В. Аносов «Взгляд на математику и нечто из нее»