Презентация на тему: Подготовка к контрольной работе по алгебре

Подготовка к контрольной работе по алгебре .9 класс

Тематика контрольной работы №4 (17.02.2009)Умение сравнивать рациональные числа.Преобразование числовых выражений, содержащих квадратные корни.Умение выполнять сокращение алгебраической дроби.Преобразование числовых выражений, содержащих степени с целым показателем.Решение линейных уравнений.Умение раскладывать квадратный трехчлен на множители.Решение квадратных неравенств.Представление о графике квадратичной функции.Интерпретация графика реальной зависимости.Умение решать квадратные уравнения с параметром.

Итоговый слайдСравнение рациональных чиселПреобразование числовых выражений, содержащих квадратные корни.Сокращение алгебраической дроби.Преобразование числовых выражений, содержащих степени с целым показателем.Решение линейных уравнений.Разложение квадратного трехчлена на множители.Решение квадратных неравенств.Представление о графике квадратичной функции.Интерпретация графика реальной зависимости.Решение квадратных уравнений с параметром.

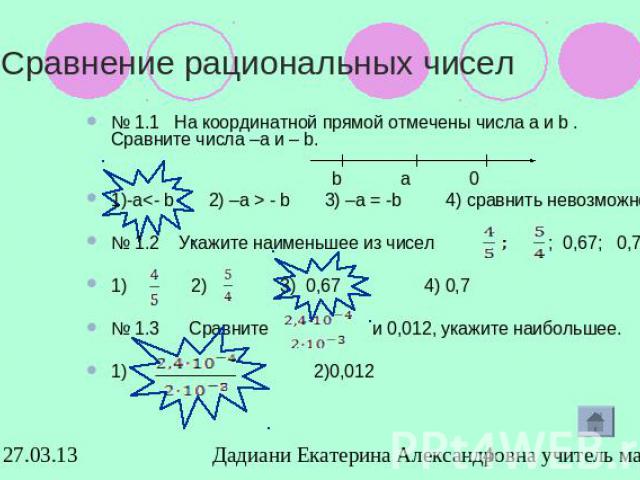
Сравнение рациональных чисел№ 1.1 На координатной прямой отмечены числа а и b . Сравните числа –а и – b. b а 0 1)-а<- b 2) –а > - b 3) –а = -b 4) сравнить невозможно№ 1.2 Укажите наименьшее из чисел ; 0,67; 0,7.1) 2) 3) 0,67 4) 0,7№ 1.3 Сравните и 0,012, укажите наибольшее.1) 2)0,012

Преобразование числовых выражений, содержащих квадратные корни.№ 2.1 Упростите выражение Ответ:№2.2 Найдите значение выражения 1)30 2)40 3)120 4)12

Сокращение алгебраической дроби.№ 3.1 Сократите дробь Ответ:№3.2 Сократите дробь Ответ:№3.3 Сократите дробь Ответ:

Преобразование числовых выражений, содержащих степени с целым показателем.№4.1 Вычислите:Ответ: №4.2 Вычислите: Ответ:

Решение линейных уравнений.№5.1 Решите уравнение: 2х-5(х+3)=12Ответ:№5.2Решите уравнение:Ответ:

Разложение квадратного трехчлена на множители.№ 6.1 Разложите на множители квадратный трехчлен 4х2-3х-1Ответ:№6.2 Разложите на множители квадратный трехчлен 4х2+20х+25Ответ:

Решение квадратных неравенств.№7.1 Решите неравенство: х2 9 Ответ:№7.2 Решите неравенство:х2 -5х 0Ответ:№7.3 Решите квадратное неравенство: х2 -5х+4 0Ответ:

Представление о графике квадратичной функции.№8.1 Укажите координаты вершины параболы у=х2 -6х -7.Ответ:№8.2 Укажите верный набор неравенств для дискриминанта и коэффициентов а, в, с, если на рисунке изображен график функции у=ах2+вх+с. стр771)а 0 2) а 0 3) а 0 4)а 0 в 0 в 0 в 0 в 0 d= 0 d 0 d 0 d = 0 с 0 с 0 с = 0 с = 0

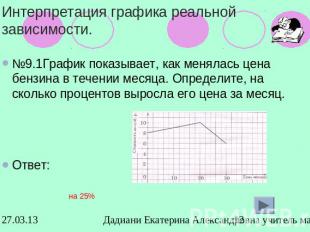
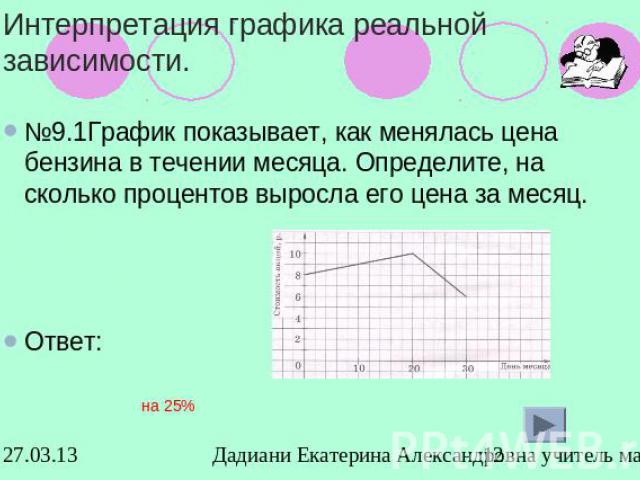
Интерпретация графика реальной зависимости.№9.1График показывает, как менялась цена бензина в течении месяца. Определите, на сколько процентов выросла его цена за месяц. Ответ:

Интерпретация графика реальной зависимости.№9.2 На рисунке изображен график движения автомобиля из пункта В в пункт А и автобуса из пункта В в пункт А . На сколько километров в час скорость автомобиля больше скорости автобуса? Ответ:

Решение квадратных уравнений с параметром.№ 10.1 При каких значениях а корни уравнения х2 -2ах +(а+1)(а-1)=0 принадлежат промежутку ? Ответ:

Решение квадратных уравнений с параметром.№10.2 При каких значениях в уравнение х2 +2(в+1)х +9=0 имеет два различных положительных корня?Ответ:( ) №10.3 При каком значении т сумма квадратов корней уравнения х2 +(2-т)х –т-3=0 минимальна?Ответ:

Решение 10.1Д=4а2-4(а+1)(а-1)=4а2-4(а2-1)=4а2-4а2+4=4=22х1,2=х1=-а+1 и х2=-а-1, тогда <=><=> => аОтвет:

Решение 10.2Решение: Д=4(в+1)2-4⋅9=4((в+1)2-92)=4(в+1-3)(в+1+3)=4(в-2)(в+4)Так как уравнение должно иметь два различных корня х1 и х2 , его дискриминант должен быть положительным ( Д 0), тогда 4(в-2)(в+4) По теореме Виета имеем: х1 +х2 = - 2(в+1)х1⋅х2 =9, так как по условию х1 >0 и х2 >0, то - 2(в+1)>0 и 9>0. –b-1 , b -1 b<Ответ: ( )

Решение 10.3По теореме Виета имеем: х1+ х2= - (2-т)х1⋅ х2 = - т-3.х1 2+ х2 2= х1 2+ х2 2+2 х1 х2 - 2 х1 х2=( х1+ х2)2 - 2 х1 х2, тогда(-2+т)2 – 2( -т -3)=т2-4т+4+2т+6=т2-2т+10=т2-2т+1+9=(т-1)2+9 – минимальна при т-1=0, значит при т=1.Ответ: 1.

успехов на контрольной работе!!!