Презентация на тему: Преобразования графиков функций

Преобразования графиков функций 10 класс

Авторы: Галеев Наиль Якупова Лилия - ученики 10 Б класса ФМЛ № 38 г.Ульяновска Руководитель работы: Алейникова Татьяна Владимировна - учитель математики

Говоря о преобразованиях графиков функций, мы имеем ввиду изменения графика некой элементарной функции (график которой строится достаточно просто) относительно системы координат с помощью параллельного переноса, симметрии относительно осей координат, растяжения или сжатия вдоль оси. «Элементарные» функции:

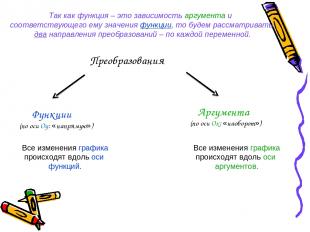
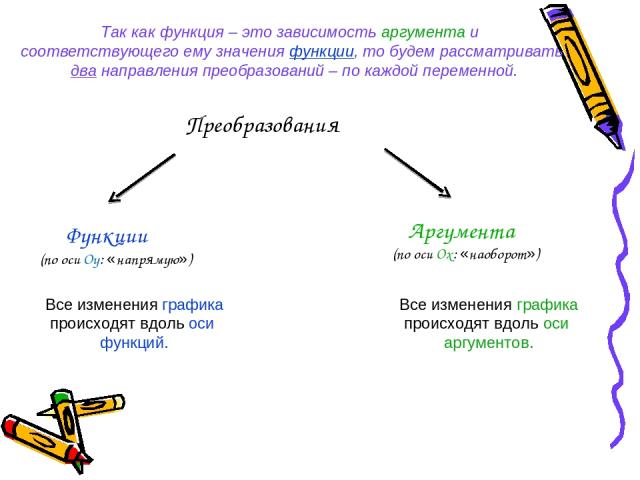
Преобразования Функции (по оси Оу: «напрямую») Аргумента (по оси Ох: «наоборот») Все изменения графика происходят вдоль оси функций. Все изменения графика происходят вдоль оси аргументов. Так как функция – это зависимость аргумента и соответствующего ему значения функции, то будем рассматривать два направления преобразований – по каждой переменной.

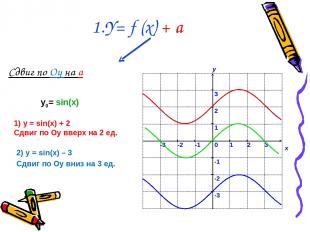
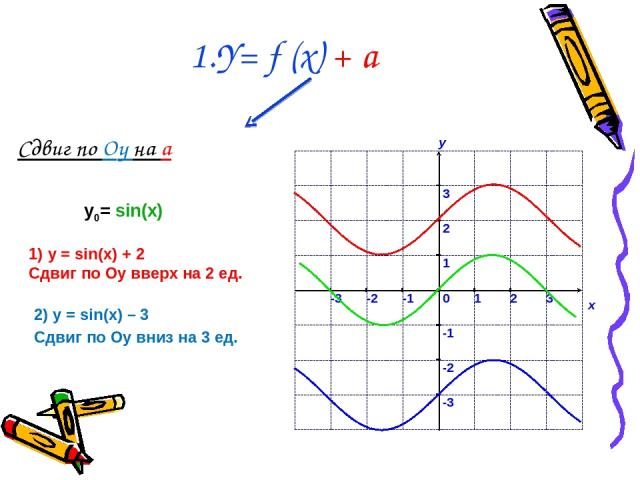
Сдвиг по Оy на a 1.Y= f (x) + a 1) у = sin(x) + 2 Сдвиг по Оу вверх на 2 ед. 2) у = sin(x) – 3 Сдвиг по Оу вниз на 3 ед. у0= sin(x)

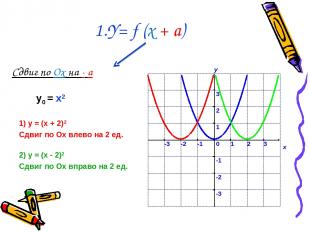
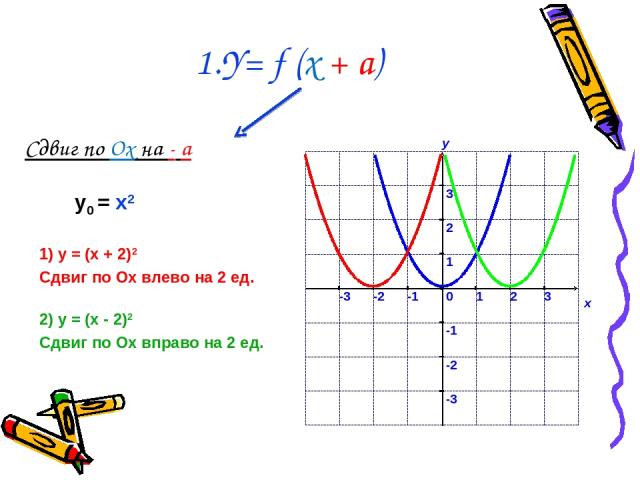
1.Y= f (x + a) Сдвиг по Ox на - a 1) у = (x + 2)2 Сдвиг по Ох влево на 2 ед. 2) у = (x - 2)2 Сдвиг по Ох вправо на 2 ед. у0 = x2

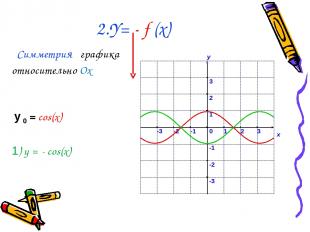
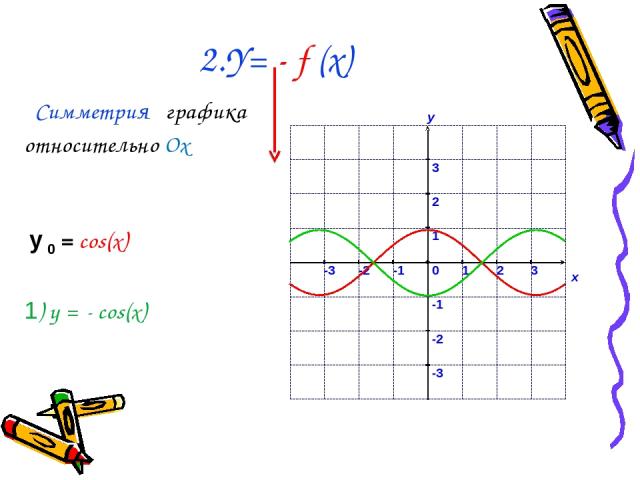
2.Y= - f (x) Симметрия графика относительно Ох у 0 = cos(x) 1) у = - cos(x)

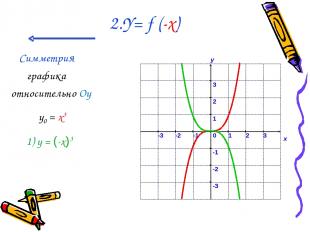
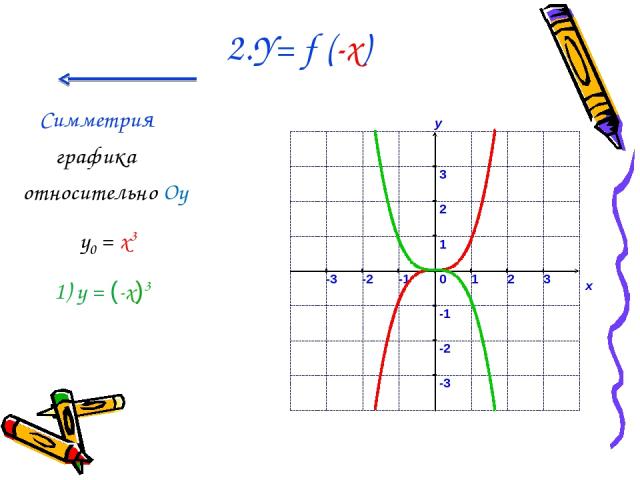
2.Y= f (-x) Симметрия графика относительно Oy у0 = x3 1) у = (-x)3

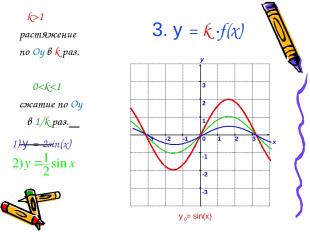
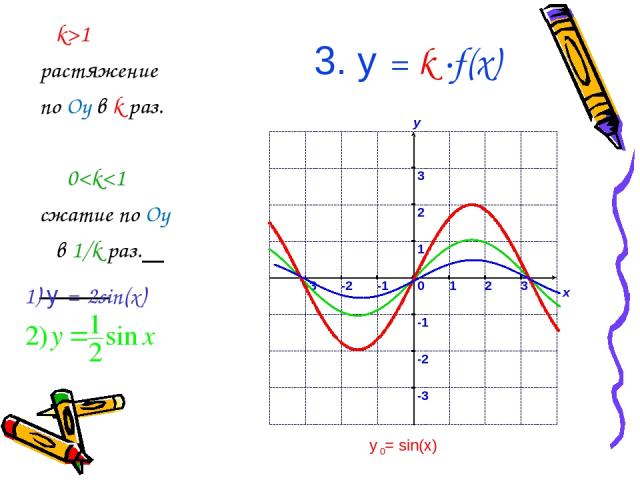
3. у = k ∙f(x) k>1 растяжение по Oy в k раз. 0

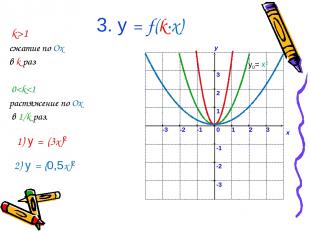
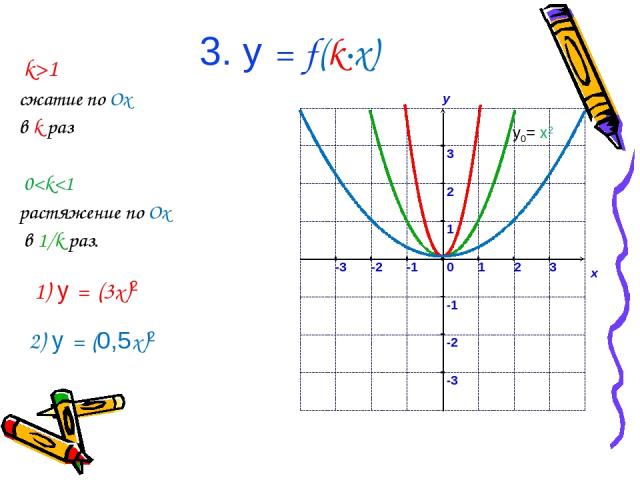
3. у = f(k∙x) k>1 сжатие по Ox в k раз 0

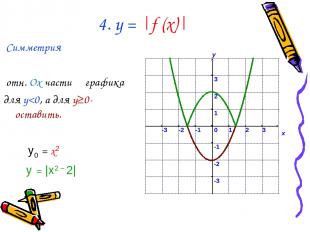
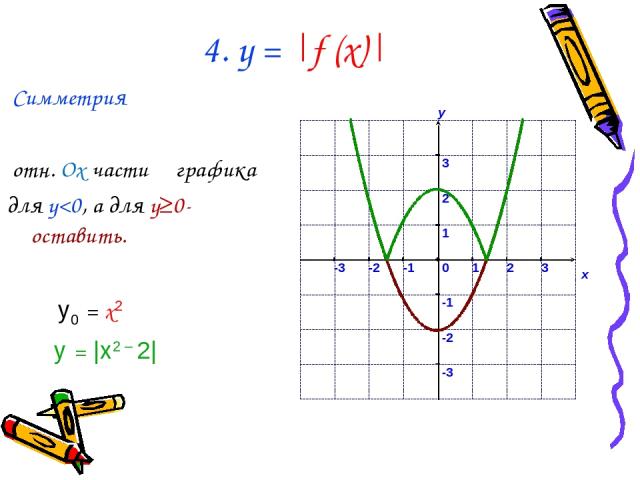
4. у = |f (x)| Симметрия отн. Ox части графика для y

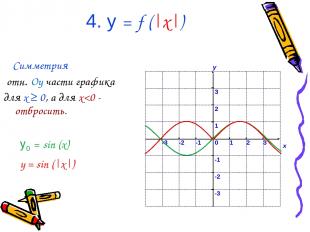
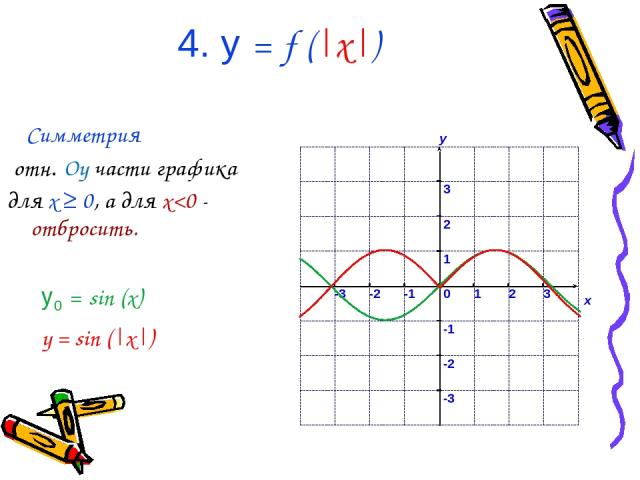
4. у = f (|x|) Симметрия отн. Oy части графика для x ≥ 0, а для x

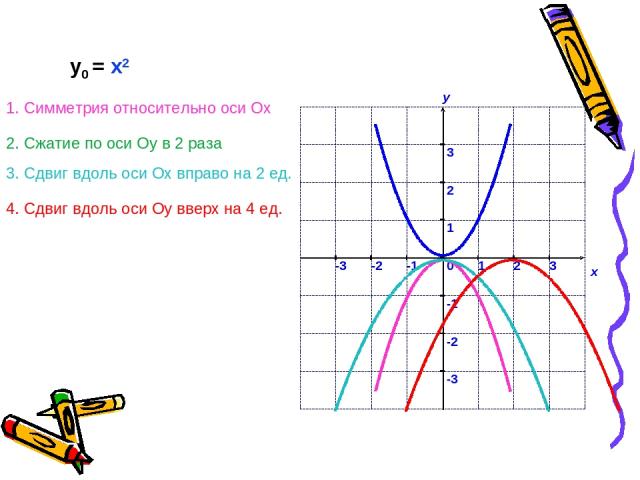
В зависимости от задания функции ее график можно построить в результате композиции нескольких последовательно выполненных преобразований. Для этого в правой части формулы, задающей функцию, надо расставить порядок действий как в обычном примере: У = - 0,5•(х – 2)2 + 4 Учитывая, что от перестановки мест множителей произведение не меняется, выполняем преобразования в следующей последовательности: 1. Симметрия относительно оси Ох (× (-1)) 2. Сжатие по оси Оу в 2 раза (× 0,5) 3. Сдвиг вдоль оси Ох вправо на 2 ед.( – 2) 4. Сдвиг вдоль оси Оу вверх на 4 ед.( + 4) у0 = x2 2 3 1 4 1 2 3 4 или у = -1• 0,5•(х – 2)2 + 4

у0 = x2 1. Симметрия относительно оси Ох 2. Сжатие по оси Оу в 2 раза 3. Сдвиг вдоль оси Ох вправо на 2 ед. 4. Сдвиг вдоль оси Оу вверх на 4 ед.

Применение преобразований графиков – очень увлекательный процесс. Это не только экономия времени при построении, но и эстетическое наслаждение, а также ощущение своей «власти» над Функцией, график которой «податлив» в умелых руках и легко «подчиняется» воле знающего! Заключение: