Презентация на тему: Исследование функций и построение графиков

Исследование функций и построение графиков

Теоретический материал

Содержание 1) Область определения функции2) Свойства функции (четность, нечетность, периодичность)4) Точки пересечения функции с осями координат5) Непрерывность функции. Характер точек разрыва6) Асимптоты7) Экстремумы функции. Исследование функции на монотонность8) Выпуклость функции. Точки перегиба

Область определения функции Определение. Областью определения функции называется множество значений независимой переменной, при которых функция определена.Примеры.

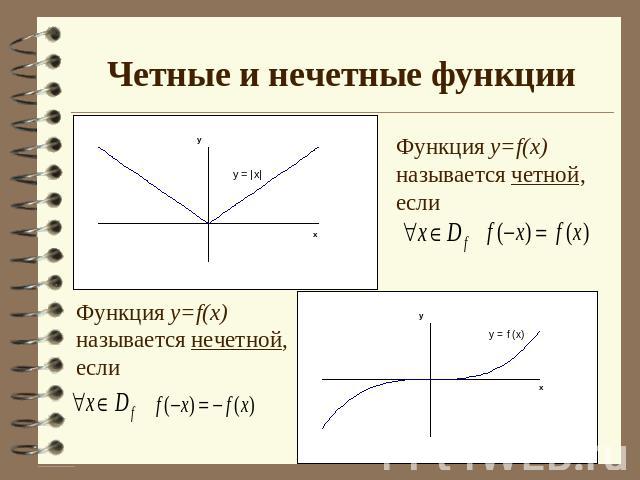
Четные и нечетные функции Функция y=f(x) называется четной, еслиФункция y=f(x) называется нечетной, если

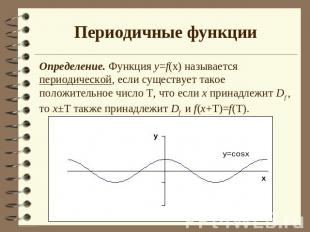
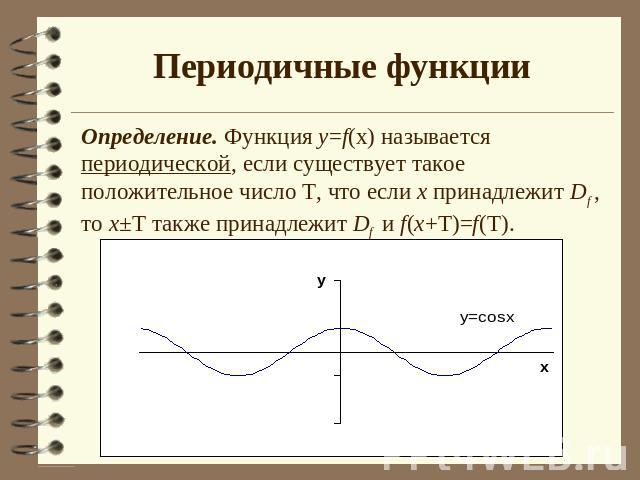
Периодичные функции Определение. Функция y=f(x) называется периодической, если существует такое положительное число Т, что если х принадлежит Df , то х±Т также принадлежит Df и f(x+T)=f(T).

Точки пересечения с осями координат При исследовании функции необходимо найти координаты точек пересечения графика функции с осями координат. Абсциссы точек пересечения графика функции с осью Ох находятся из системы уравнений у=f(x) и у=0, а ординаты точек пересечения графика функции с осью Оу находятся из системы уравнений у=f(x) и х=0.

НепрерывностьХарактер точек разрыва Функция у=f(x) называется непрерывной в точке х0, если функция определена в точке х0 и предел функции в точке х0 равен значению функции в точке х0. Функции, непрерывные в каждой точке из области определения функции, называются непрерывными функциями. Примеры непрерывных функций: y=cosx, y=sinx, y=ex , y=Pn(x) (многочлен степени n).

Точки разрыва функции Определение. Точкой разрыва функции называется точка из области определения функции, в которой функция не является непрерывной.Пример. Функция

Классификация точек разрываТочки устранимого разрыва Если в точке х0 существуют конечные односторонние пределы функции, равные между собой, но не равные значению функции в точке х0, то точка х0 называется точкой устранимого разрыва.

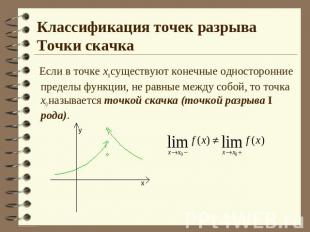
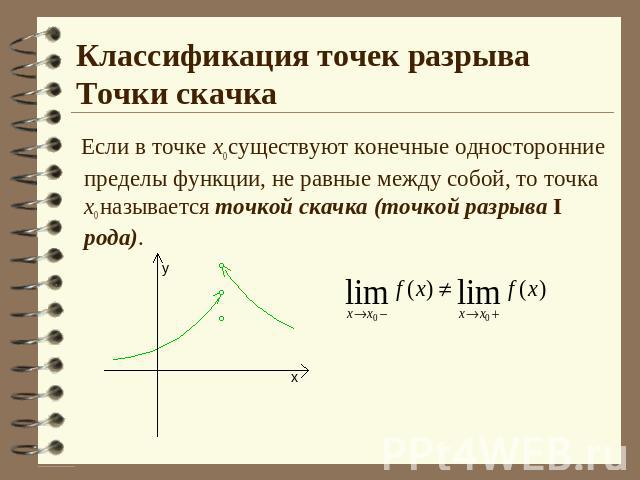
Классификация точек разрываТочки скачка Если в точке х0 существуют конечные односторонние пределы функции, не равные между собой, то точка х0 называется точкой скачка (точкой разрыва I рода).

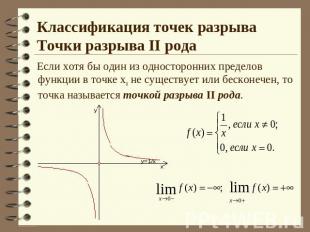
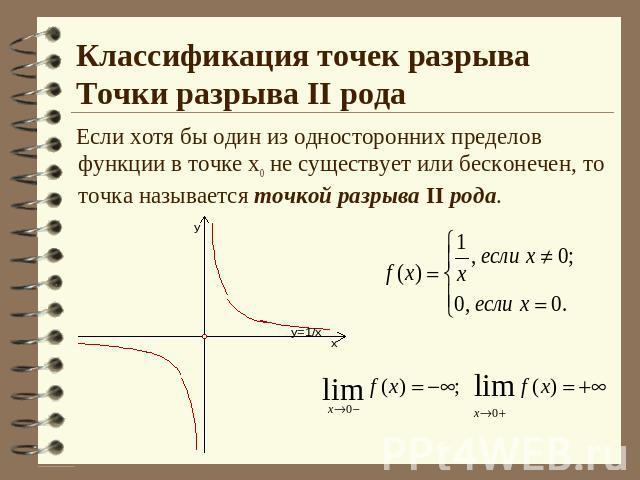
Классификация точек разрываТочки разрыва II рода Если хотя бы один из односторонних пределов функции в точке х0 не существует или бесконечен, то точка называется точкой разрыва II рода.

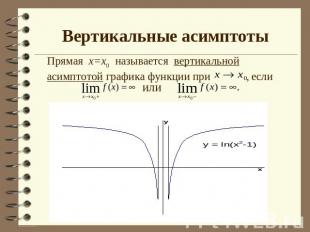
Вертикальные асимптоты Прямая х=х0 называется вертикальной асимптотой графика функции при , если

Наклонные асимптоты

Экстремумы функции Пусть функция f (x) определена и непрерывна на интервале (а, b). Точка х0 интервала (а, b) называется точкой строгого максимума (минимума) функции f (x), если в некоторой проколотой окрестности точки х0 f (x)< f (x0) ( f (x) > f (x0) ). Точки минимума и точки максимума функции называются точками экстремума функции. Необходимое условие экстремума. Пусть точка х0 - точка экстремума функции. Тогда либо производная функции в этой точке равна 0, либо не существует.

Исследование функции на монотонность Известно, что если f '(x)>0 (f '(x)>0) в (а, b), то функция f (x) строго возрастает (строго убывает) в (а, b). Рассмотрим функцию f(x) = x + 1|xКритические точки функции х=±1. f '(x)>0 при х<-1 и при х>1; f '(x)<0 при -1<x<0 и при 0<x<1.

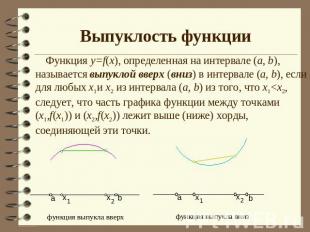
Выпуклость функции Функция у=f(х), определенная на интервале (а, b), называется выпуклой вверх (вниз) в интервале (а, b), если для любых х1и х2 из интервала (а, b) из того, что х1<х2, следует, что часть графика функции между точками (х1,f(х1)) и (х2,f(х2)) лежит выше (ниже) хорды, соединяющей эти точки.

Выпуклость функции.Точки перегиба Также говорят, что график функции f (x) имеет на интервале (a, b) выпуклость, направленную вниз (вверх), если график этой функции в пределах (a, b) лежит не ниже (не выше) любой своей касательной. Если график функции в точке (х0, f(x0)) переходит с одной стороны касательной на другую, то точка х0 называется точкой перегиба функции f(x).

Достаточные условия выпуклости функции и существования точек перегиба Достаточное условие строгой выпуклости функции Если на интервале (а,b) f ''(x)>0, то на интервале (а,b) функция выпукла вниз, и если на интервале f ''(x)<0, то на интервале (а,b) функция выпукла вверх.Достаточное условие строгой выпуклости функции Если в левой и правой полуокрестностях некоторой точки х0 f ''(x) имеет противоположные знаки, то точка х0 – точка перегиба функции.

Практический материал

1). Поскольку знаменатель положителен при всех , область определения функции - вся ось 2). Функция f(x) - нечётная, поскольку при смене знака x числитель меняет знак, а знаменатель остаётся без изменения, откуда f(-x) = - f(x). Следовательно, график функции симметричен относительно начала координат. Периодической функция не является. 3). Поскольку область определения этой элементарной функции -- вся вещественная ось, вертикальных асимптот график не имеет.

4). Найдём наклонные асимптоты при в виде . Имеем: Таким образом, асимптотой как при , так и при служит прямая .

5). Найдём точки пересечения с осями координат. Имеем: f(0) = 0, причём x=0 - единственное решение уравнения f(x) = 0. Значит, график y = f(x) пересекает сразу и ось Ox, и ось Oy в начале координат. Очевидно, что f(x)>0 при x>0 и f(x)<0 при x<0.

6) Найдём производную: Очевидно, что f´(x) ≥ 0 при всех ; единственная точка, в которой f´(x) = 0 - это x=0. Значит, функция f(x) возрастает на всей оси Ox, а в стационарной точке x=0 имеет горизонтальную касательную.

7) Найдём вторую производную: Знаменатель этой дроби положителен при всех x. Числитель имеет корни x=0 и x=±√3, при этом f’’(x)>0 на интервалах и - на этих интервалах функция выпукла. На интервалах и выполняется обратное неравенство f’’(x)<0, здесь функция вогнута. Все три точки, в которых f’’(x)=0, то есть точки - √3, 0, √3, являются точками перегиба.

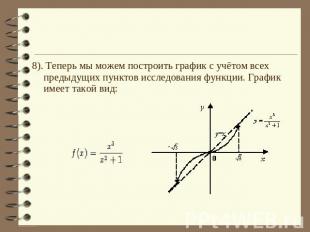
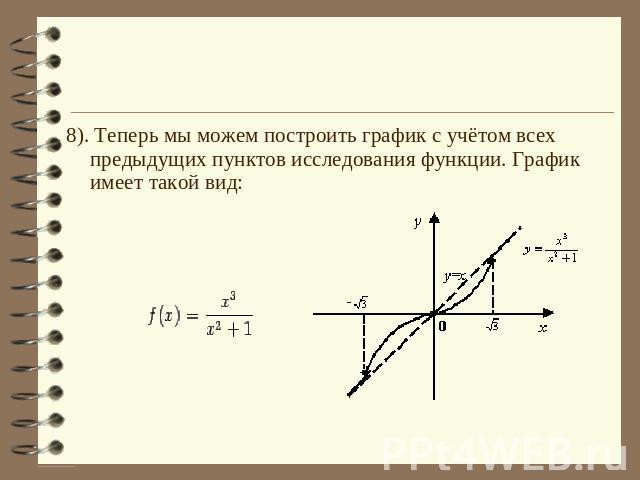
8). Теперь мы можем построить график с учётом всех предыдущих пунктов исследования функции. График имеет такой вид:

Исследуем функцию f(x) = (x2 – 2x)ex и построим её график. 1). Ясно, что D(f) = R, поскольку оба сомножителя в выражении f(x) определены при любом . Область значений E(f) найдём после того, как отыщем локальные экстремумы функции. 2). Функция не является ни чётной, ни нечётной; не является она и периодической. 3). Область определения не имеет граничных точек, значит, нет и вертикальных асимптот графика.

4) Будем искать наклонные асимптоты в виде y = kx + b. Коэффициент k найдём по формуле : при имеем так что при асимптоты нет, причём функция f(x) стремится к при .При имеем:

Теперь найдём значение b по формуле . Имеем: Таким образом, k=0 и b=0, так что при асимптота имеет уравнение y=0, то есть совпадает с осью Ox. 5). Точка пересечения с осью Oy равна f(0)=0. Заодно нашли одну точку пересечения с осью Ox. Чтобы найти все точки пересечения графика с осью Ox, решаем уравнение f(x) = (x2 – 2x)ex . Поскольку ex ≠ 0, решаем уравнение , откуда получаем два корня: x=0 и x=2. Так как точек разрыва нет, то имеем три интервала знакопостоянства функции: , и .

Знак функции определяется множителем x2 – 2x, поскольку ex >0 при всех x. Значит, f(x)>0 при и при и f(x)<0 при . 6) Вычислим производную: Интервалы возрастания задаются неравенством f‘(x)>0, то есть, с учётом того, что ex >0, неравенством x2 – 2x>0. Решением этого неравенства служит множество На этих двух интервалах функция возрастает. Легко видеть, что на интервале выполняется неравенство f‘(x)<0, следовательно, это интервал убывания функции. В точке -√2 возрастание сменяется убыванием, значит, точка   -√2 - точка локального максимума.

Значение функции в этой точке равно В точке √2 убывание сменяется возрастанием, значит, точка √2 -- точка локального минимума функции. Значение функции в точке минимума таково: Теперь мы можем примерно представить, как идёт график функции: Эскиз графика функции f(x)

Становится очевидно, что область значений функции -- это 7) По эскизу графика видно, что где-то в местах, обведённых кружочками, должно смениться направление выпуклости, то есть должны быть точки перегиба. Для исследования этого найдём вторую производную: Решим неравенство , эквивалентное неравенству x2+2x-2>0. Решением этого квадратного неравенства служит объединение интервалов и . На этих интервалах функция выпукла.

Ясно, что на интервале функция будет вогнутой. Тем самым точки и   -- это точки перегиба. Значения функции в точках перегиба такие: 8). Осталось построить окончательный чертёж: График функции (x2 – 2x)ex .