Презентация на тему: Классическое определение вероятности

Классическое определениевероятности Проект подготовила: учитель математики и физики Павловской ООШ Луховицкого района Московской областиКартамышева Юлия Николаевна

Тема: Классическое определение вероятностиЦель: -создать условия для осознания и осмысления блока новой учебной информации.Задачи: -Способствовать запоминанию основной терминологии, умению устанавливать события вероятности; -формировать умение упорядочить полученные знания для рационального применения;-развитие навыков учащихся в вычислении классической вероятности;-формирование вероятностного мышления; -способствовать развитию интереса к математике; -умений применять новый материал на практике и в жизни.

Истинная логика нашего мира – правильный подсчет вероятностей. (Джеймс Максвелл) Возникновение первых представлений о шансах, случайности и вероятности, первых элементов статистического анализа традиционно ассоциируют с тремя факторами: распространением азартных игр, развитием астрономических исследований и появлением страхования. Правда, первый точно датированный контракт по страхованию жизни был подписан в Генуе в 1347 г; что же касается азартных игр, то они были широко распространены ещё в Древнем Египте (ок. 3500 г. до н.э.), не говоря уже о Древней Греции и Древнем Риме. Однако первые попытки математического анализа шансов игроков появились лишь в XVI в. и принадлежали Л. Пачоли, Н. Тарталье и Дж. Кардано; так возникла комбинаторика. Её последующее развитие связано с именами Б. Паскаля (“Трактат об арифметическом треугольнике”, 1654 г.), Г.В. Лейбница (“Рассуждение о комбинаторном искусстве”, 1666) и особенно Я. Бернулли (“Искусство предположений”, изд. в 1713 г.

Французский математик, создатель теории чисел и один из основателей математического анализа. Будучи по профессии юристом, состоял на государственной службе: с 1631 по 1648 был уполномоченным по приему прошений, а с 1648 и до конца жизни – советником парламента Тулузы. Был известен как знаток классической литературы, лингвист и поэт. Математика всегда была для Ферма лишь увлечением, и тем не менее он заложил основы многих ее областей: аналитической геометрии, исчисления бесконечно малых, теории вероятностей. Ферма не оставил ни одной законченной работы, и большинство его набросков не было опубликовано при жизни. Ферма переписывался с Р. Декартом по вопросам аналитической геометрии и был первым, кто воспользовался ее методами применительно к трехмерному пространству.Ферма Пьер (17.8.1601- 12.01.1665), французский математик.

Христиан Гюйгенс (1629-1695) его работы относятся к механике, физике, математике, астрономии. В 1651 году Гюйгенс опубликовал работу об определении длины дуг окружности, эллипса и гиперболы. Через три года появился его труд "Об определении величины окружности", который способствовал развитию теории определения отношения длины окружности к диаметру (вычисление числа пи). Затем последовал ряд других математических трактатов. Его сочинение "О расчетах при игре в кости", опубликованное в 1657 году, является одним из первых исследований в области теории вероятностей.

Пьер-Симон Лаплас (фр. Pierre-Simon Laplace; 23 марта 1749 — 5 марта 1827) — французский математик и астроном; известен работами в области небесной механики, дифференциальных уравнений, один из создателей теории вероятностей. Заслуги Лапласа в области чистой и прикладной математики и особенно в астрономии громадны: он усовершенствовал почти все отделы этих наук.

Во главе русской математики середины и второй половины XIX века стоял Пафнутий Львович Чебышев (1821-1894). Чебышев был воспитанником Московского университета, который он окончил в 1841 году. В этом учебном заведении Чебышев защитил и магистерскую диссертацию "Опыт элементарного анализа теории вероятностей", и данная область стала одним из основных предметов его научных занятий.

Муавр Абрахам (26.5.1667-27.2.1754)-английский математик. Член Лондонского королевского общества (1697г.). Родился в Витри-ле-Франсуа (Франция). Учился у французского математика Ж. Озанама. Прожил много лет в Лондоне. Труды по теории рядов, теории вероятностей, теории комплексных чисел. В теории вероятностей доказал важную теорему, названную его именем, и включаемую теперь во все учебники по этой теории. В теории комплексных чисел вывел правила возведения в степень и извлечения корня n-й степени из комплексных чисел, которые широко применяются в тригонометрии и алгебре при решении двучленных уравнений (формулы Муавра), Иностранный член Парижской и Берлинской Академии Наук.

Байес (Бейес) Томас (1702-7.4. 1761)-английский математик, член Лондонского королевского общества (1742г.). Родился в Лондоне. Получил домашнее образование. Математические исследования Бейеса относятся к теории вероятностей. Поставил и решил одну из основных задач элементарной теории вероятностей (теорема Бейеса). Соответствующая работа была опубликована в 1763г. Формула Бейеса, позволяющая оценить вероятность событий эмпирическим путем, играет важную роль в современной теории вероятностей и математической статистике. Другая его работа "Очерки к решению проблемы доктрины шансов" была опубликована в 1958г. Сохранилась терминология: бейесовский подход к статистическим законам, бейесовская оценка решения и другие.

Пуассон Симеон Дени (21.6.1781-25.4.1840)- французский математик, физик, механик. Член Парижской Академии наук (1812). Существенное значение имеют работы Пуассона, посвященные определенным интегралам, уравнениям в конечных разностях, дифференциальным уравнениями с часиными производными, теории вероятностей, вариационному исчислению, рядам. Основательно улучшил способы применения теории вероятностей вообще и к вопросам статистики в частности, а также доказал теорему, которая касалась закона больших чисел (закон Пуассона), впервые воспользовавшись терминов "закон больших числе".

«Предмет математики настолько серьезен, что полезно не упускать случаев, делать его немного занимательным».Б. Паскаль Паскаль (Pascal) Блез (19.6.1623, Клермон-Ферран, — 19.8.1662, Париж), французский религиозный философ, писатель, математик и физик. Родился в семье высокообразованного юриста, занимавшегося математикой и воспитывавшего своих детей под влиянием педагогических идей М. Монтеня, рано проявил выдающиеся математические способности, войдя в историю науки как классический пример отроческой гениальности.

А. Н. Колмогоров (1903-1987) – величайший русский математик ХХ столетия, создатель современной теории вероятностей, автор классических результатов в теории функций, в математической логике, топологии, теории дифференциальных уравнений, функциональном анализе, в теории турбулентности, теории гамильтоновых систем. Созданные им школы в теории вероятностей, теории функций, функциональном анализе и теории гамильтоновых систем определили развитие этих направлений математики в ХХ столетии. В истории российской науки его имя стоит рядом с именами М. В. Ломоносова, Д. И. Менделеева - ученых, всей своей жизнью прославивших Россию.

«…Все в природе подлежит измерению, все может быть сосчитано».Н. И. Лобачевский Классическая вероятность события

Какова вероятность того, что из 5 цыплят один будет синего цвета?

ПРИМЕРЫНа экзамене -24 билета. Андрей не разобрался в одном билете и очень боится его вытянуть. Какова вероятность, что Андрею достанется несчастный билет?А- достанется несчастливый билетn=24; m =1, тогда Р(А)=В лотереи 10 выигрышных билетов и240 билетов без выигрыша. Какова вероятность выиграть в эту лотерею, купив один билет?А- выиграть Исходов всего 240+10=250; Шансы=10; Р(А)= В лотереи 100 билетов, из них 5 выигрышных. Какова вероятность проигрыша А- проиграть: Исходов 100; Шанс =100-5=95, тогда Р(А)=

Ошибка Даламбера Какова вероятность, что подброшенные вверх две правильные монеты упадут на одну и ту же сторону? Решение, предложенное Даламбером. Опыт имеет три равновозможных исхода: Обе монеты упали на «орла».Обе монеты упали на «решку».Одна из монет упала на «орла», другая на «решку». N = 3; N(A) = 2; P(A) =

Правильное решение. Орел, орелРешка, решкаОрел, решкаРешка, орелN = 4; N(A) = 2; P(A) = Нельзя объединять два принципиально разных исхода в один. Природа различает все предметы.

Некоторые факты о Кубике Рубика.Число возможных различных состояний кубика Рубика равно 43 252 003 274 489 856 000. Это число не учитывает то, что ориентация центральных квадратов может быть разной. С учётом ориентации центральных квадратов количество состояний получается в 46/2=2048 раз больше, а именно88 580 102 706 155 225 088 000 состояний.

Задание 1.Какие из следующих событий – случайные, достоверные, невозможные:черепаха научиться говорит;вода в чайнике, стоящим на горячей плите закипит;ваш день рождения – 19 октябрядень рождение вашего друга – 30 февраля;вы выиграете участвуя в лотереи;вы не выигрываете, участвуя в беспроигрышной лотереи;вы проиграете партию в шахматы;на следующей недели испортиться погода;вы нажали на звонок, а он не зазвонил;после четверга будет пятница;после пятницы будет воскресенье.

Задание 2.Для каждого из перечисленных событий определите, какое оно: достоверное, возможное, невозможное:летом у школьников будут каникулы;5 июля в Иркутске будет солнечно;после уроков дежурные уберут кабинет;в 11-м классе школьники не будут изучать алгебру;зимой выпадает снег;при включении света, лампочка перегорит;вы выходите на улицу, а на встречу вам идет слон.

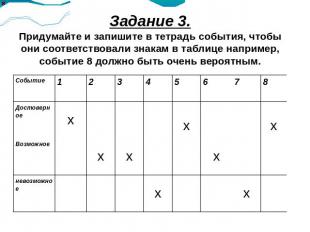
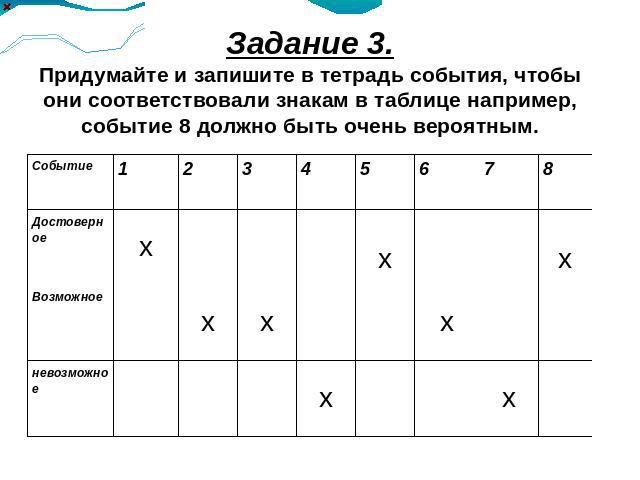
Задание 3.Придумайте и запишите в тетрадь события, чтобы они соответствовали знакам в таблице например, событие 8 должно быть очень вероятным.

Подведение итогов: Что такое событие?Какое событие называют действительным?Какое событие называют случайным?Какое событие называют невозможным?Какие ученые занималась поиском закономерностей в случайных событиях?

Домашнее задание:1.Составить 2 задачи на вероятность.2.Написать реферат на одну из тем: Даниил Бернулли и его вклад в развитие теории вероятностей.Гюйгенс и его вклад в развитие теории вероятностейБлез Паскаль и его вклад в развитие теории вероятностей Ферма и его вклад в развитие теории вероятностей

Литература Ю.Н.Макарычев, Н.Г.Миндюк. Начальные сведения из теории вероятностей в школьном курсе алгебры. “Математика в школе”. № 7. 2004 г. стр. 24.В.А.Булычев, Е.А.Бунимович. Изучение теории вероятностей и статистики в школьном курсе математики. “Математика в школе”. № 4. 2003 г. стр. 59.Электронные источники информации Бунимович Е.А., Булычев В.А. Вероятность и статистика 5-9. Электронное учебное пособие на CD-ROM. – М.: Дрофа, 2003.www.teorver.ru http://ru.wikipedia.org/wiki/Теория_вероятности

Спасибо за внимание!