Презентация на тему: Классическое определение вероятности. Комбинаторные методы решения задач

Классическое определение вероятности.Автор Минасян Людмила ГригорьевнвМБОУ СОШ №2 г. Горячий Ключ

Цель урока: Выработать умение решать задачи на определение классической вероятности с использованием основных формул комбинаторики.Оборудование: карточки, коробка с шарами, карточки с буквами, интерактивная доска.

1 этап:проверка домашнего заданияВ урне находится 3 синих, 8 красных и 9 белых шаров одинакового размера и веса, неразличимых на ощупь. Шары тщательно перемешаны. Какова вероятность появления синего, красного и белого шаров при одном вынимании шара из урны?

РЕШЕНИЕ К ЗАДАЧЕ№ 1:Так как появление любого шара можно считать равновозможным, то мы имеем всего n= 3+8+9 =20 элементарных событий. Если через А, В, С обозначить события, состоящие в появлении соответственно синего, красного и белого шаров, а через m1 , m2 , m3 –благоприятствующих этим событиям случаев, то ясно, что m1=3, m2=8, m3=9.Поэтому Р(А) = , Р(В)= , Р(С) = .

Задача Наташа купила лотерейный билет, который участвует в розыгрыше 100 призов на 50000 билетов, а Лена – билет, который участвует в розыгрыше трех призов на 70000 билетов. У кого больше шансов выиграть?

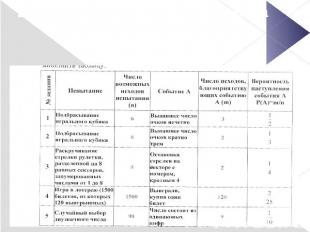
2 этап: Самостоятельная работа Правильные ответы к таблице.

4 этап: Практикум по решению задач. Задача 1Таня забыла последнюю цифру номера телефона знакомой девочки и набрала ее наугад. Какова вероятность того, что Таня попала к своей знакомой?

Решение:На последнем месте может стоять одна из 10 цифр: от 0 до 9. Значит, n=10, m=1, Р(А)=

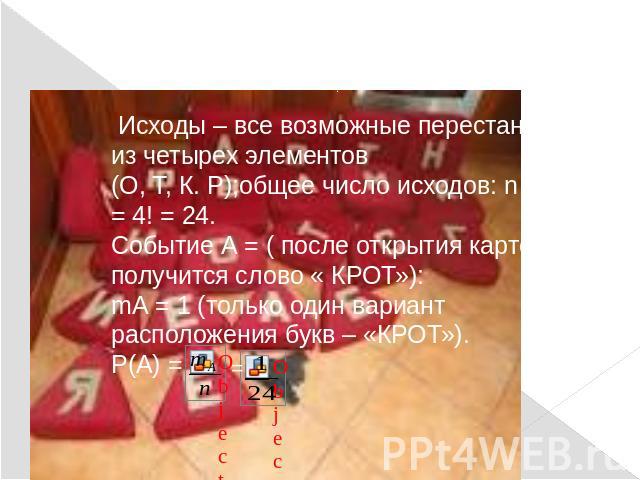
Задача 2.На четырех карточках написаны буквы О, Т, К, Р. карточки перевернули и перемешали. Затем открыли наугад последовательно эти карточки и положили в ряд. Какова вероятность того, что получится слово «КРОТ»?

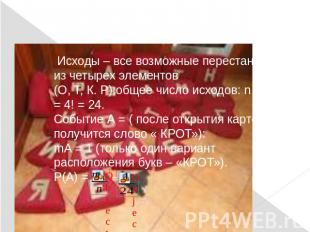
Решение: Исходы – все возможные перестановки из четырех элементов (О, Т, К. Р);общее число исходов: n = Р4 = 4! = 24.Событие А = ( после открытия карточек получится слово « КРОТ»):mА = 1 (только один вариант расположения букв – «КРОТ»).Р(А) =

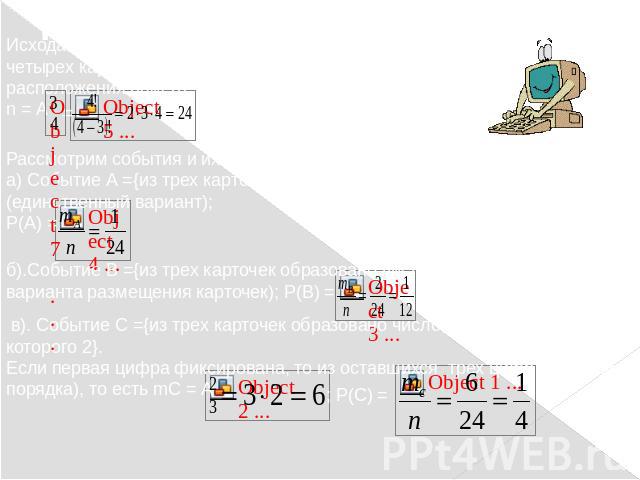
Задача 3:На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем наугад открыли последовательно три карточки и положили в ряд.Какова вероятность того, что в результате получилось: а) число 123; б) число 312 или 321; в) число, первая цифра которого 2?

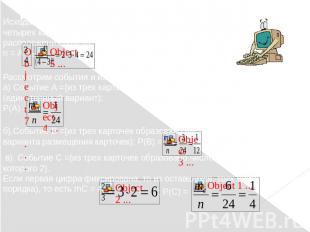
Решение:Исходами опыта являются все возможные размещения четырех карточек на трех местах (порядок расположения важен). Общее число исходов: n = АРассмотрим события и их вероятности:а) Событие А ={из трех карточек образовано число 123}, mА = 1 (единственный вариант);Р(А) = б).Событие В ={из трех карточек образовано число 312 и 321}, mB =2 (два варианта размещения карточек); Р(В) =в). Событие С ={из трех карточек образовано число, первая цифра которого 2}.Если первая цифра фиксирована, то из оставшихся трех цифр ( с учетом порядка), то есть mC = А

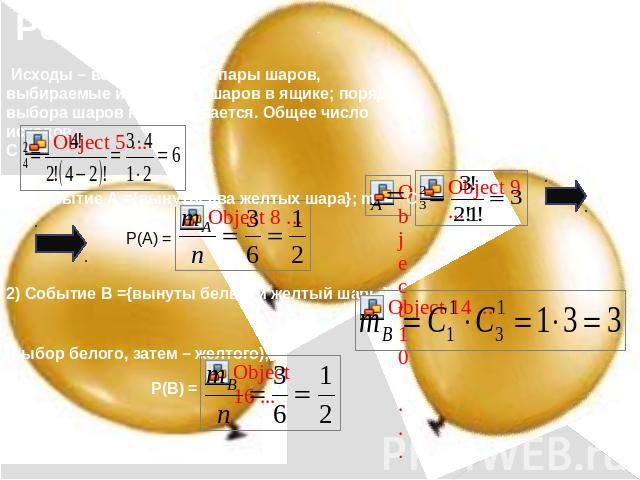
Задача 4:В ящике лежат 1 белый шар и три желтых шара. Наугад вынимают два шара. Какова вероятность того, что вынуты: 1) 2 желтых шара; 2) белый и желтый шары?

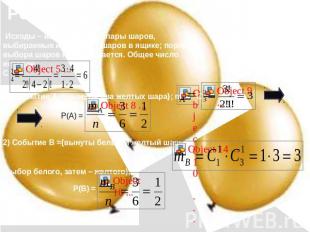
Исходы – все возможные пары шаров, выбираемые из четырех шаров в ящике; порядок выбора шаров не учитывается. Общее число исходов С1). Событие А ={вынуты два желтых шара}; m2) Событие В ={вынуты белый и желтый шары}; (выбор белого, затем – желтого);

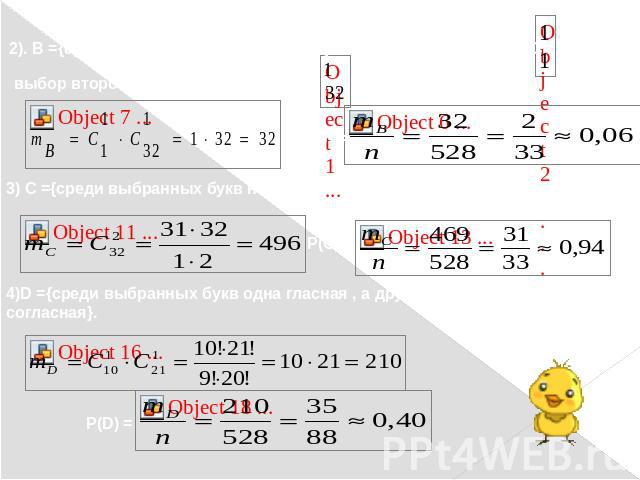
Задача 5:Случайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите вероятности того, что:1)обе они согласные;2)среди них есть «ъ»;3)среди них нет «ъ»;4)одна буква гласная, а другая согласная.

Решение:Исходы – все возможные пары букв русского алфавита без учета порядка их расположения; общее число возможных исходов 1). А ={обе выбранные буквы - согласные}. Поскольку в русском языке 21 согласная, то событию А благоприятствует mA = C

2). В ={среди выбранных букв есть «ъ»}. Выбор твердого знака С выбор второй буквы из оставшихся С3) С ={среди выбранных букв нет буквы « ъ»;4)D ={среди выбранных букв одна гласная , а другая согласная}.

Домашнее задание:Набирая номер телефона, состоящий из 7 цифр, абонент забыл, в какой последовательности идут три последние цифры. Помня лишь, что это цифры 1, 5 и 9, он набрал первые четыре цифры, которые знал, и наугад комбинацию из цифр !, 5 и 9. Какова вероятность того, что абонент набрал правильный номер?Решение:исходы – перестановки из трех элементов (1, 5, 9); общее число исходов:n=Р3 =3! = 6.

Задача2:На каждой карточке написана одна из букв О, П, Р, С, Т. Несколько карточек наугад выкладывают одну за другой в ряд. Какова вероятность, что при выкладывании:1)3-х карточек получится слово РОТ;2)4-х карточек получится слово СОРТ;3)5-ти карточек получится слово СПОРТ?Исходами опыта будут расположения выбранных карточек в определенном порядке, то есть размещения

конец урока спасибо за внимания…