Презентация на тему: "Исследование функций и построение их графиков"

Алгебра и начала математического анализа 11 класс «Исследование функций и построение их графиков»

Автор презентации: учитель математики МБОУ«Малошильнинская СОШ» Тукаевского района Республики Татарстан Киямова Фируза Мухамматовна

Алгоритм исследования функции Для исследования функции необходимо пройти следующие этапы:

1. Находим область определения функции: 1. Находим область определения функции: D(f)=? Областью определения функции y=f(x), заданной аналитически, называют множество всех действительных значений независимой переменной х, для каждого из которых функция принимает действительные значения.

Находим область изменения функции: Областью изменения функции f(х) называют множество всех чисел f(х), соответствующих каждому х из области определения функции.

Если f(-x)=f(x), то функция f(x) называется четной. График четной функции симметричен относительно оси ординат (оси Oy). Если f(-x)=f(x), то функция f(x) называется четной. График четной функции симметричен относительно оси ординат (оси Oy). Если f(-x)=-f(x), то функция f(x) называется нечетной. График нечетной функции симметричен относительно начала координат.

3.Выясняем периодичность функции Если f(x+T)=f(x) при некотором T>0, то функция y=f(x) называется периодической. График периодической функции имеет одну и ту же форму на каждом из отрезков …, [-2T; -T], [-T; 0], [0; T], [T; 2T], … . Поэтому достаточно построить график на каком-нибудь одном таком отрезке и затем воспроизвести полученную кривую на остальных отрезках.

4. Находим точки максимума и минимума функции и интервалы возрастания и убывания (интервалы монотонности). Для этого: вычисляем производную f’(x) и находим критические точки функции, т.е. точки, в которых f’(x)=0 или не существует; определяя знак производной, находим интервалы возрастания и убывания функции: если f’(x)>0, то функция возрастает, если f’(x)<0, то функция убывает; если производная меняет знак при переходе через критическую точку xo є D, то xo – точка экстремума: если производная меняет знак с «минуса» на «плюс» – то xo – точка минимума, если же с «плюса» на «минус» – то точка максимума. Если производная сохраняет знак при переходе через критическую точку, то в этой точке экстремума нет.

5. Находим точки перегиба функции и интервалы выпуклости вверх/вниз. Для этого: вычисляем вторую производную f’’(x) и находим точки, принадлежащие области определения функции, в которых f''(x)=0 или не существует; определяя знак второй производной, находим интервалы выпуклости и вогнутости: если f’’(x)<0, то график функции имеет выпуклость вверх, если f’’(x)>0, то график функции имеет выпуклость вниз; если вторая производная меняет знак при переходе через точку xo є D, в которой f''(x)=0 или не существует, то xo – точка перегиба.

6. Находим асимптоты функции. Вертикальные: находим односторонние пределы в граничных точках или . Если такие пределы существуют, то прямая х=а является вертикальной асимптотой графика функции у=f(x)  Наклонные асимптоты: Если выполняется условие lim (f(x) – (kx + b)) = 0, x   то прямая у = kx + b является асимптотой функции у = f(x) при x. Коэффициенты k и b можно найти следующим образом:   k = b = (f(x) - kx)

7. Есть ли у функции промежутки, где она возрастает (убывает)? f’(x)> 0, функция возрастающая f’(x)<0, функция убывающая

8. Есть ли у нее промежутки знакопостоянства? f’(x) = 0 на промежутке, => функция f(х) постоянная на этом промежутке. Если в точке xo производная меняет знак c «+» на «-», то xo - точка локального максимума; Если в точке xo производная меняет знак с «-» на «+», то xo - точка локального минимума.

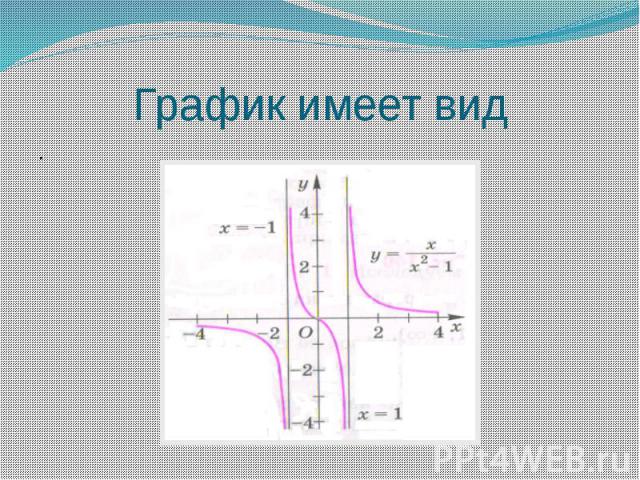
Пример у= х/х²-1 1. Знаменатель выражения х/(х2 – 1) обращается в нуль при х= -1 и при х = 1, поэтому D(f) = (-∞;-1)U(-1; 1) U (1; +∞). 2. Е(f) = R (видно из дальнейшего исследования) 3. f(-х) = -f(х) - функция нечетная. 4. Функция непериодическая. 5. Производная функции в области определения: f '(x) =( )' = - и f '(x) < 0 во всей области определения =>функция непрерывна и возрастает во всей области определения, точек локального экстремума нет. 6. f’’(x) = 2х(х² + 3)/( х²-1) ³ обращается в нуль в точке х=0

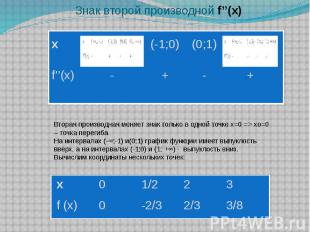
Знак второй производной f’’(x)

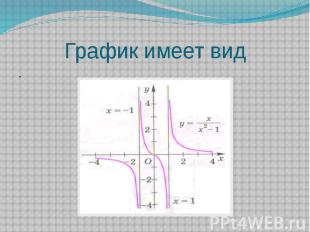
График имеет вид .