Презентация на тему: Построение графиков функций с использованием производной

Построение графиков функций с использованием производной.

Основные понятия

1. Область определения функции -множество всех значений, которые может принимать аргумент, т.е. множество значений х, для которых можно вычислить у, если функция задана формулой.Обозначение:

2. Область изменения функции или множество значений функции. Обозначение:

3. Точки пересечения с осями координат. Ордината точки пересечения с осью Оу находится из условияу= f(0)Абсциссы точек пересечения с осью Ох (нули функции) находятся из условия f(x) =0.
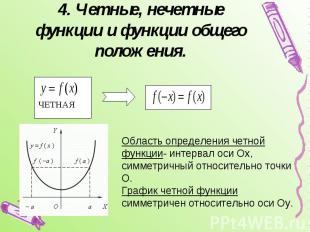
4. Четные, нечетные функции и функции общего положения. Область определения четной функции- интервал оси Ох, симметричный относительно точки О.График четной функции симметричен относительно оси Оу.

Область определения нечетной функции-интервал оси Ох, симметричный относительно точки О.График нечетной функции симметричен относительно начала координат. Функция, не являющаяся ни нечетной, ни четной, называется функцией общего положения.
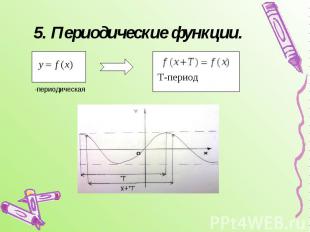
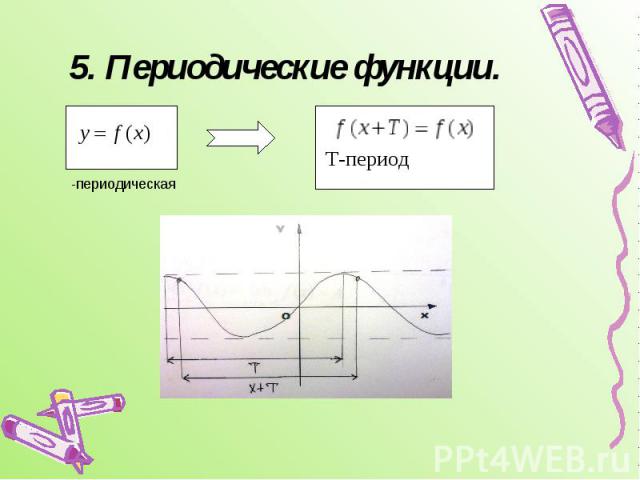
5. Периодические функции.
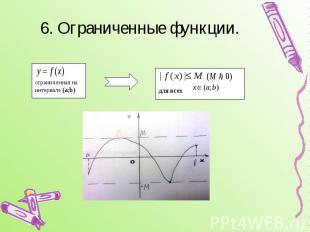
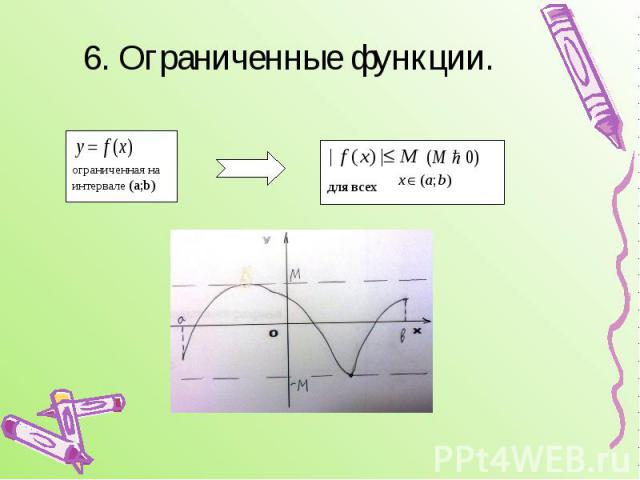
6. Ограниченные функции.

7. Точки разрыва функции и их характер. Для элементарных функций точка разрыва - это такая точка, в которой функция не определена, но определена в окрестностях этой точки.

Виды точек разрыва: -точка устранимого разрыва

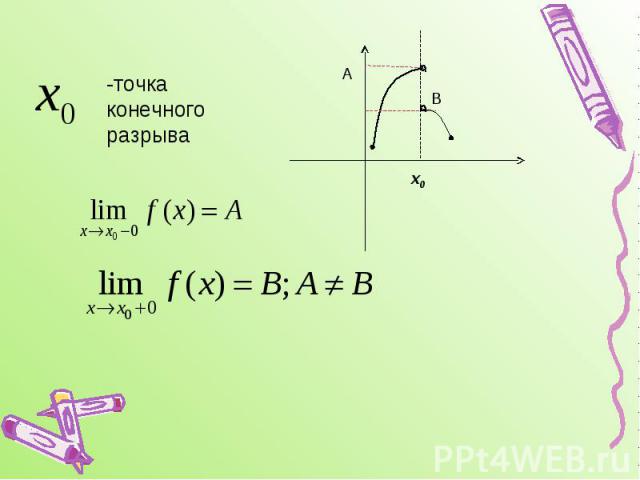
-точка конечного разрыва

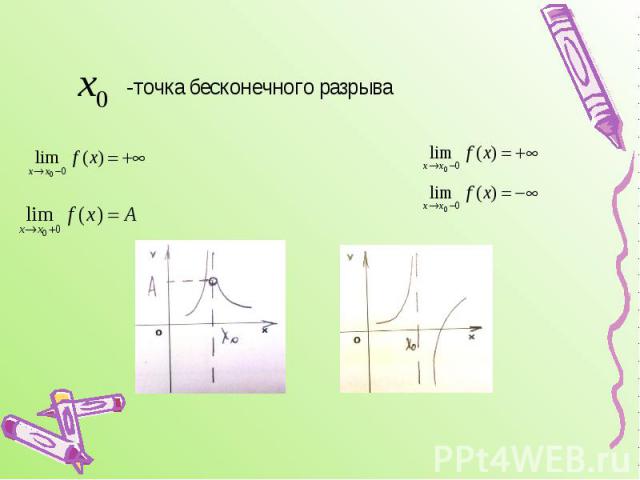
-точка бесконечного разрыва

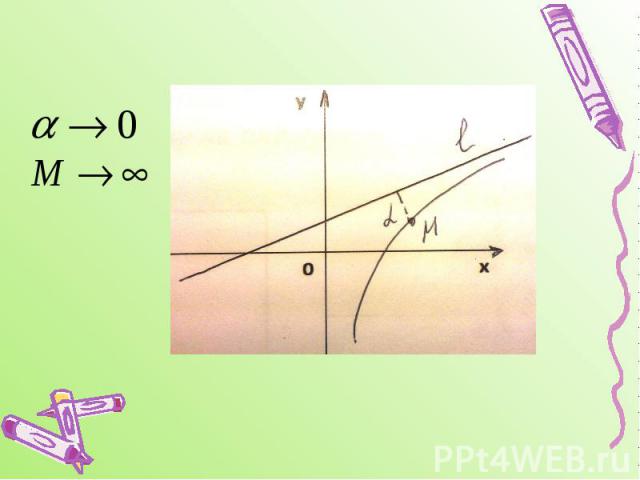
8. Асимптоты графика функций. Прямая l называется асимптотой графика функции у=f(x), еслирасстояние от точки М графика допрямой стремится к нулю приудалении точки М до кривой вбесконечность.
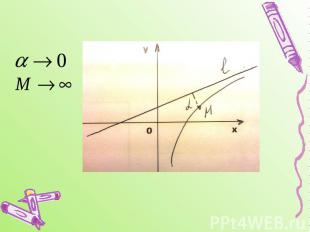

Виды асимптот ВертикальнаяГоризонтальнаяНаклонная Если f(x) можно представить в виде f(x)=kx+b+ , где , когда , то прямая y=kx+b является асимптотой: при k равном нулю - горизонтальной, при k не равном нулю- наклонной.График функции может иметь вертикальные асимптоты в точках разрыва (бесконечного) или на границах области определения функции.
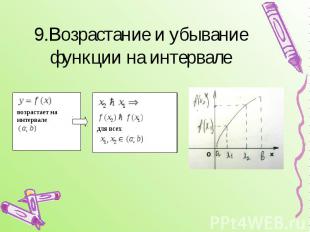
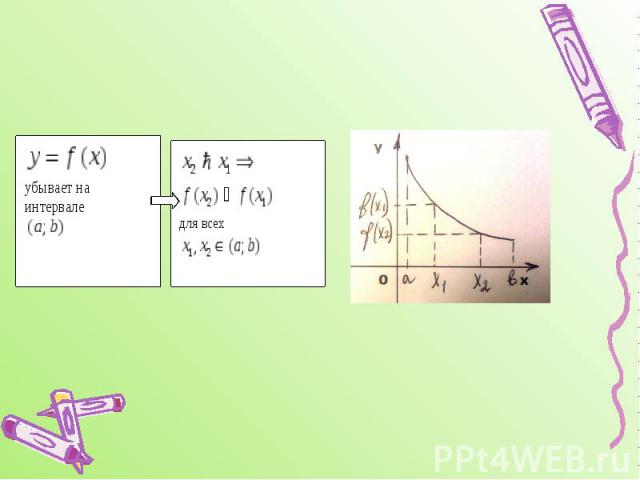
9.Возрастание и убывание функции на интервале
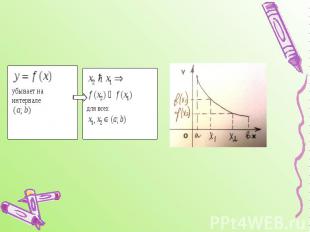

Достаточные признаки возрастания и убывания функции:
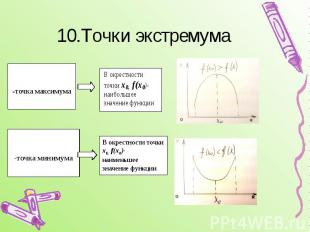
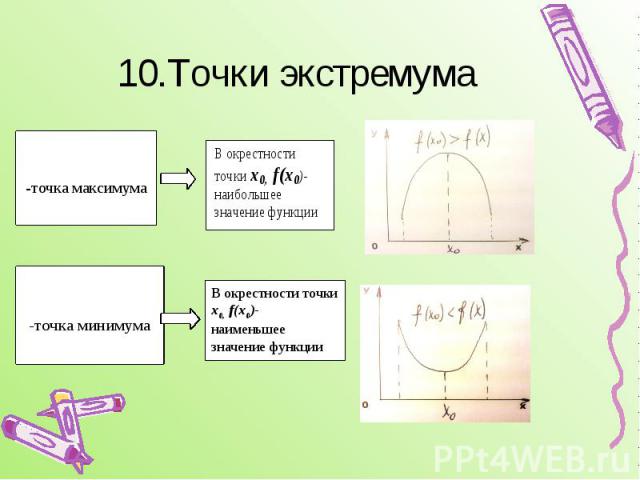
10.Точки экстремума

Достаточные признаки точки экстремума.

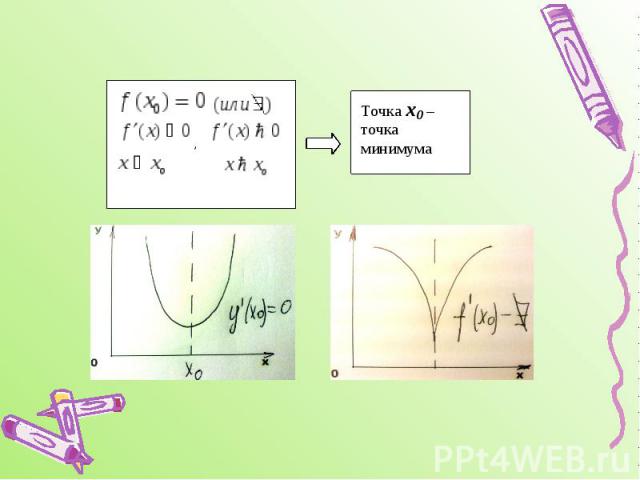
1ый достаточный признак
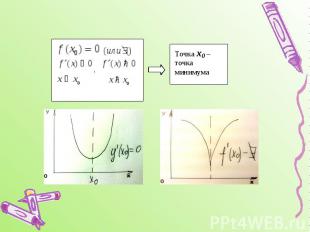

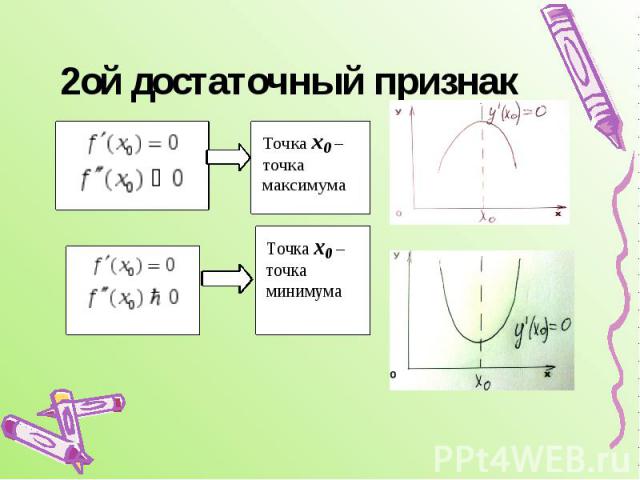
2ой достаточный признак

11.Выпуклость и вогнутость

Достаточные признаки выпуклости и вогнутости
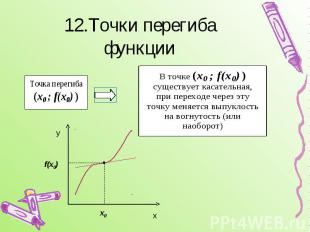
12.Точки перегиба функции

Достаточный признак точки перегиба Для построения точки перегиба необходимо установить связь между существованием производной в точке х0 и существованием касательной к графику функции в точке (х0 ; f(х0) ).

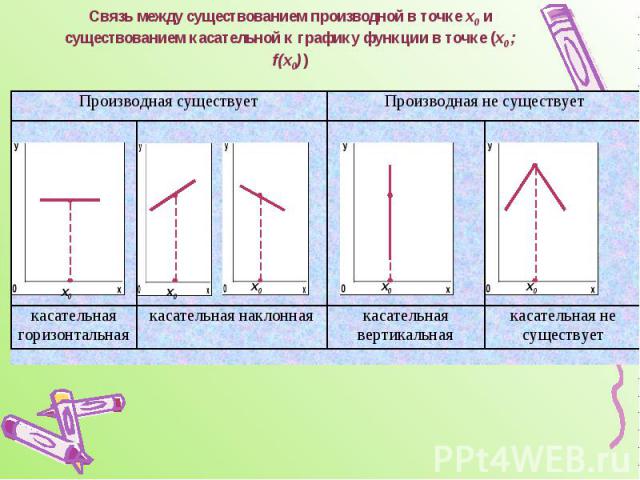
Связь между существованием производной в точке х0 и существованием касательной к графику функции в точке (х0 ; f(х0) )
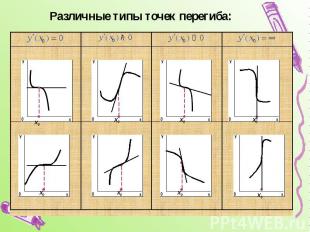
Различные типы точек перегиба:

Спасибо за внимание!