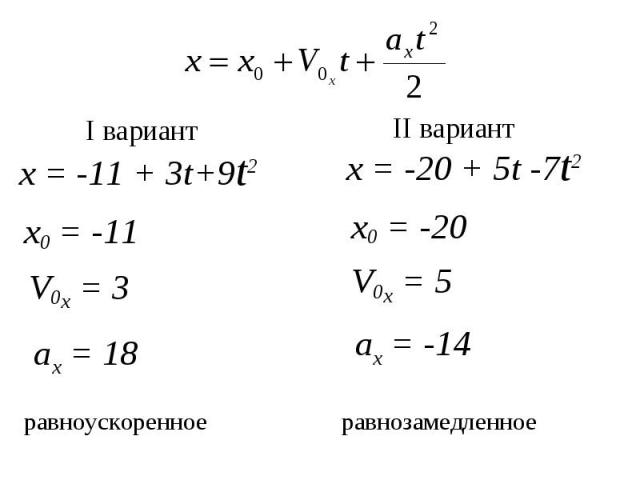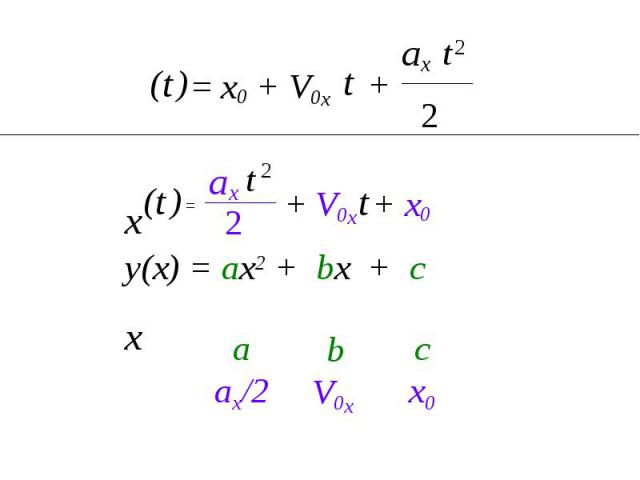Презентация на тему: Графическое изображение прямолинейного равноускоренного движения

Графическое изображение прямолинейного равноускоренного движения

Что значит «прямолинейное»? Какое движение называется равноускоренным?

Формулы проекции перемещения координаты тела

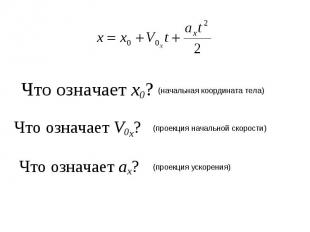
Что означает х0? (начальная координата тела) Что означает V0x? (проекция начальной скорости) Что означает ах? (проекция ускорения)

x = 15 – 4t – 2t2 x = 7,5 – 8t +16t2 х0 = 15 V0x = -4 V0x = -8 аx = -4 Определите значения начальной координаты, проекции начальной скорости, проекции ускорения и назовите вид движения. Задание №1. х0 = 7,5 аx = 32 равнозамедленное равноускоренное

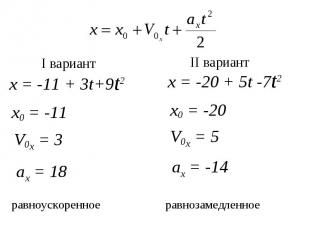
x = -11 + 3t+9t2 х0 = -11 V0x = 3 x = -20 + 5t -7t2 V0x = 5 х0 = -20 аx = 18 аx = -14 равноускоренное равнозамедленное I вариант II вариант

x ax 2 Назовите независимую переменную t = x0 + V0x t + t (аргумент) ) 2 0 х t Назовите зависимую переменную (функция) (

Назовите независимую переменную (аргумент) у ( х ) = а х + b х + с Назовите зависимую переменную (функция) 0 х у 2

Что является графиком этой функции? Как влияет знак перед старшим коэффициентом на направление ветвей? Этапы построения параболы: Найти вершину (х0; у0). х0 = -b/2a, y0 = y(x0). 2. Провести ось симметрии. 3. Определить направление ветвей. 4. Построить несколько симметричных точек. у(х) = ах2 + bx + c

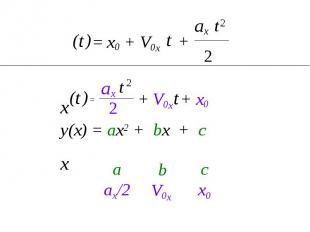
с x0 b V0x a ax/2 2 ax 2 t = x0 + V0x t + t ) ( x x t ) ( + V0x + x0 2 ax t 2 = t у(х) = ах2 + bx + c

Задача №1. Построить график координаты от времени свободного падения тела от начального уровня. x0=0 V0x = 0 gx= 9,8 м/с2 Какой вид примет уравнение функции? t ) ( x = gx t 2 2 t gx 2 t = x0 + V0x t + ) 2 ( x

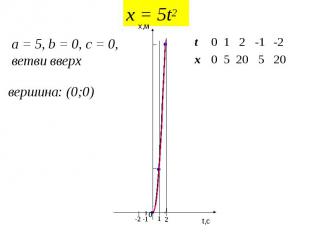
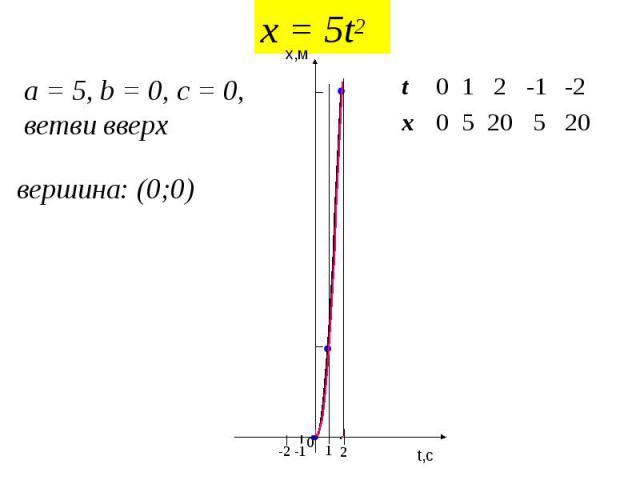
x = 5t2 a = 5, b = 0, c = 0, ветви вверх вершина: (0;0) 20 5 20 5 0 x -2 -1 2 1 0 t t,c x,м 0 1 -1 2 -2 5 20

Задача №2. Построить график функции свободного падения шарика, брошенного вверх от нулевого уровня, со скоростью 20 м/с. Каким будет движение? (равнозамедленным). 2 t + V0x t - t ) 2 ( gx x = 2 t = V0x t - t ) 2 ( gx х ax t 2 t = x0 + V0x t + ) 2 ( х

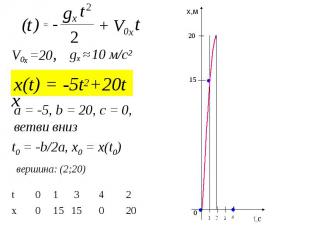
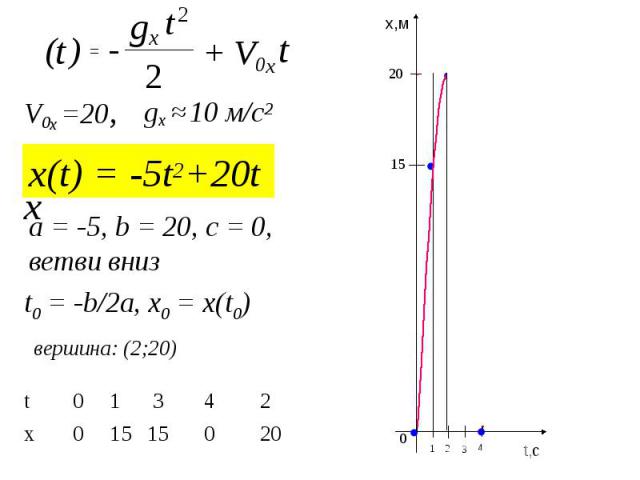
x(t) = -5t2+20t 2 t + V0x t - t ) 2 ( gx = x V0x =20, gx ≈ 10 м/с2 вершина: (2;20) a = -5, b = 20, c = 0, ветви вниз 20 0 15 15 0 x 2 4 3 1 0 t t,c x,м 0 1 2 3 4 20 15 t0 = -b/2a, x0 = x(t0)

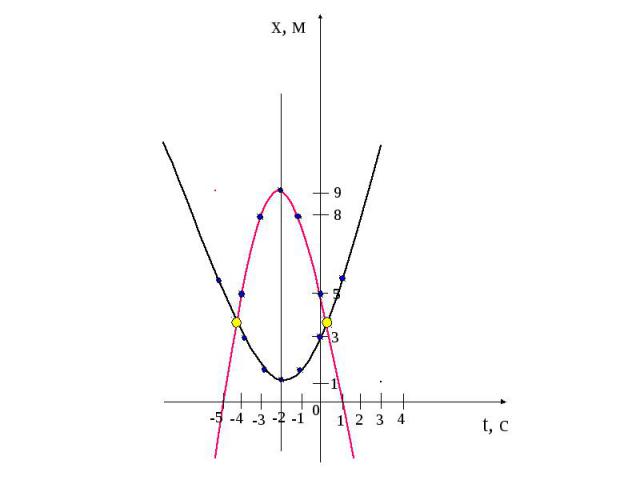
Задача №3. Движения 2-х тел заданы уравнениями х1 = 0,5t2 + 2t +3, x2 = -t2 – 4t +5 . Определите графически время и место встречи. 1. Построить график первого движения. 2. Построить график второго движения. 3. Найти точки пересечения этих графиков. Парабола х = 0,5t2, ветви вверх. Парабола х = -t2, ветви вниз. 4. Определить координаты этих точек (t, x). t - время встречи, х – место встречи.

х1 = 0,5t2 + 2t +3 вершина: t0 = -2/20,5 = -2 x0 = 0,54 - 22 + 3 = 1 (-2; 1) 1,5 1 1,5 5,5 3 x -1 -2 -3 1 0 t x2 = -t2 – 4t +5 вершина: t0 = 4/2(-1) = -2 x0 = -4 - 4(-2) + 5 = 9 (-2; 9) 0 5 8 8 5 x 1 -4 -3 -1 0 t ось симметрии: х = -2 ось симметрии: х = -2

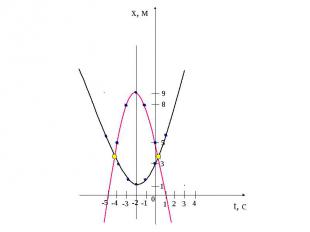
t, c x, м 4 3 2 -4 -3 -2 -1 0 1 8 5 3 9 1 -5

Точки пересечения: (0,3; 3,71) (-4,3; 3,71) Ответ: (0,3; 3,71).

Задача №4. Движения 2-х мотоциклистов заданы уравнениями: х1 = 9 + t2, х2 = 6t. 1.Охарактеризуйте движения. 2. Найдите графически время и место встречи.

Спасибо!!! Молодцы!!!