Презентация на тему: Построение графиков функций

Учебный элементНаименование: Построение графиков функций

Цели: изучив данный учебный элемент,вы сможете: 1. Находить особо важные точки графика: - стационарные и критические точки;- точки экстремума;- точки пересечения графика с осями координат;- точки разрыва функции.2. Проведя исследование функции, построить график.

Необходимое оборудование, материалы и вспомогательные средства:

Литература Мордкович А.Г. Алгебра и начала математического анализа. Часть 1. Учебник. – М., 2008.Мордкович А.Г. Алгебра и начала математического анализа. Часть 2. Задачник. – М., 2008.Колмогоров А.Н. Алгебра и начала анализа. М., 2008.Энциклопедический словарь юного математика. – М., 1989.

Схема исследования функции: Найти область определения функции;Исследовать функцию на чётность;Найти асимптоты;Найти стационарные и критические точки;Найти точки экстремума;Найти промежутки монотонности;Найти точки пересечения с осями координат;При необходимости найти дополнительные точки.

Рассмотрим пример.Построить график функции у = 1. Область определения функции это все допустимые значения аргумента: D(у) = (-∞; +∞).2. Исследуем функцию на чётность: у(х) = у(-х) – условие чётности, у(-х) = - у(х) – условие нечётности.у(х) = у(-х) = Выполняется условие нечётности, значит график симметричен относительно начала координат.

Исследуя функцию по схеме, составим таблицу.

Дополнительные точки:

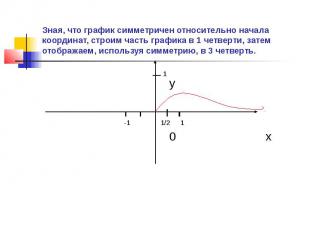
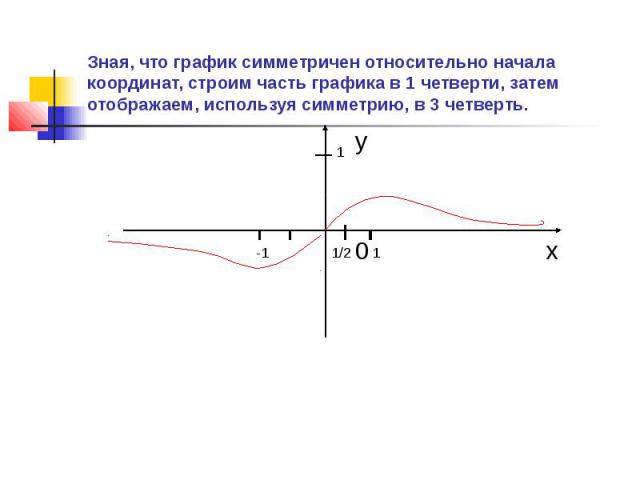
Зная, что график симметричен относительно начала координат, строим часть графика в 1 четверти, затем отображаем, используя симметрию, в 3 четверть.

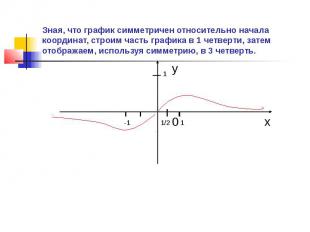
Зная, что график симметричен относительно начала координат, строим часть графика в 1 четверти, затем отображаем, используя симметрию, в 3 четверть.

1. Точки минимума и максимума это а) точки экстремума, б) стационарные точки, в) критические точки.2. Точки, в которых производная равна нулю этоа) точки экстремума, б) стационарные точки, в) критические точки.3. у(х) = у(-х) это условиеа) чётности, б) нечётности, в) возрастания функции.4. Если функция нечётная, то график симметричен относительноа) оси ОУ, б) оси Ох, в) начала координат.5.

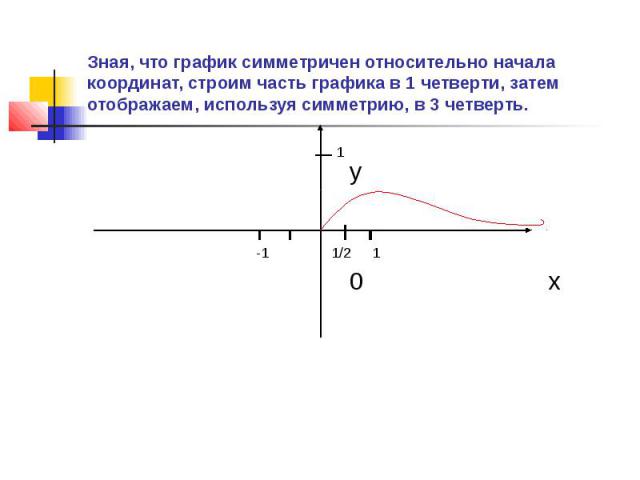
Назовите точку максимума по рисунку. 7. По предыдущему рисунку указать промежуток убывания.а ) (0,5; 2), б) [1; 2], в) (2; +∞) 8. Укажите точку разрыва графика функции у = 1/ха) х = 1, б) х = 0, в) точек разрыва нет.