Презентация на тему: Учимся решать тригонометрические неравенства

Учимся решать тригонометрические неравенства Автор: учитель высшей категории МОУ СОШ № 27Ветрова Л.И.

Решение простейшего неравенства sin х > а, где 0 < а < 1 Точки на окружности единичного радиуса, соответству-ющие аргументу х, расположены выше прямой y = a или на самой прямой. Из рисунка 1 видно, что arcsin а + 2Пn

Решение простейшего неравенства sin х > а, где -1 < а < 0 При - 1 < а < О точки , соответствующие аргументу х на окружности единичного радиуса, расположены выше прямой у = а или на самой прямой. Очевидно, что эта дуга по длине больше полуокружности и из рис. 2 видно, что arcsin а + 2Пк < х


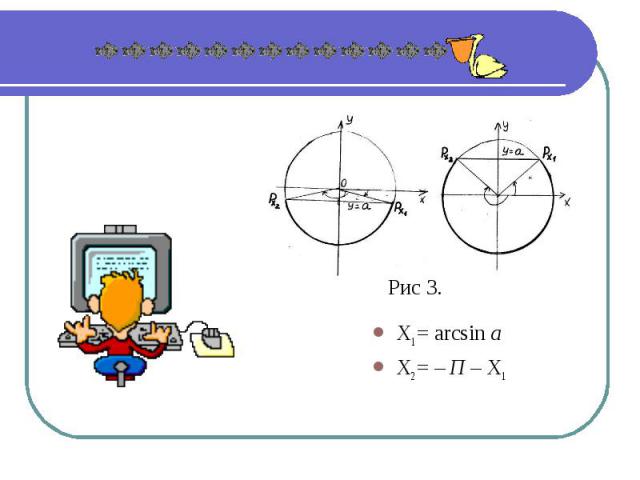
Решение неравенства sin x < a. Точки на единичной окружности, которые соответствуют аргументу х, расположены ниже прямой у = а или на самой прямой. В общем виде решения неравенства могут быть записаны в виде – П - arcsin а + 2Пn
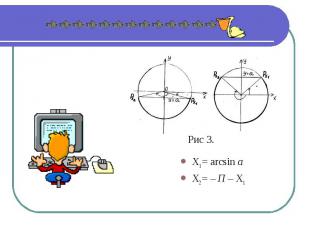
X1 = arcsin аX2 = – П – X1

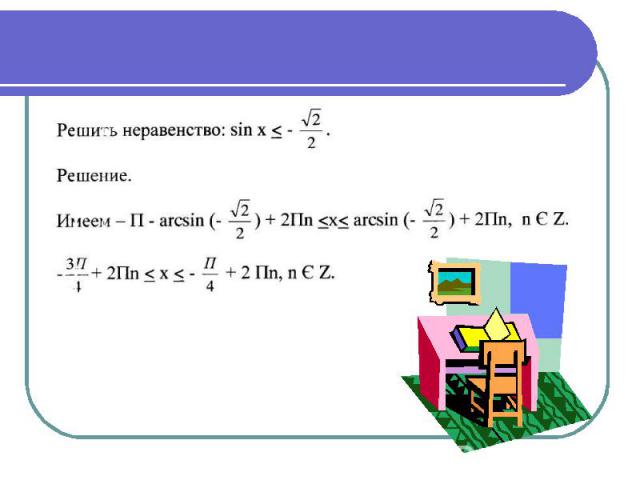
ПРИМЕР 2
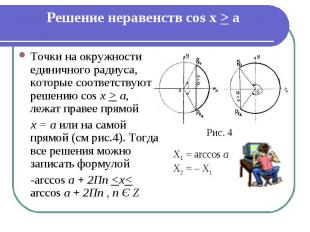
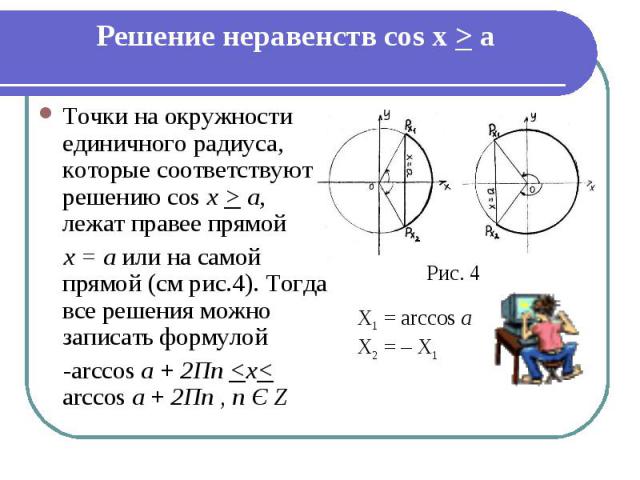
Решение неравенств cos x > a Точки на окружности единичного радиуса, которые соответствуют решению cos х > а, лежат правее прямой х = а или на самой прямой (см рис.4). Тогда все решения можно записать формулой -arccos а + 2Пn

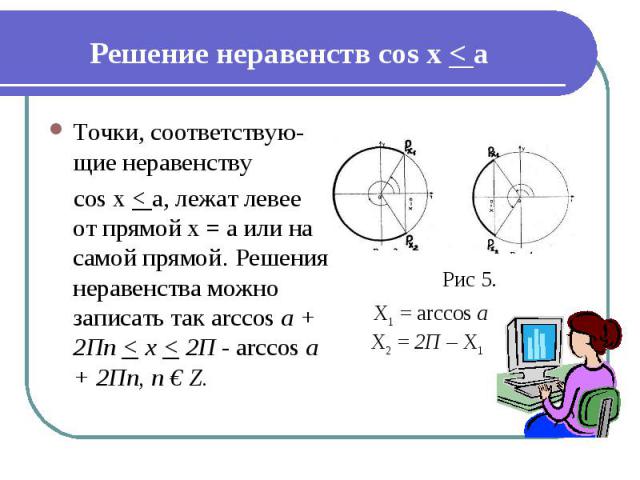
Решение неравенств cos x < а Точки, соответствую-щие неравенству cos x < а, лежат левее от прямой х = а или на самой прямой. Решения неравенства можно записать так arccos а + 2Пn < х < 2П - arccos а + 2Пn, п € Z.

ПРИМЕР 3

Решения неравенства tg х > а Все решения неравенства tg х > а задаются неравенством arctg a + Пn < x < + Пn, n Є Z

Решения неравенства tg х < а Все решения неравенства tg x < a задаются формулой- + Пk < x < arctg a + Пk, k Є Z

ПРИМЕР 4

ВНИМАНИЕ !!!