Презентация на тему: Неравенства с двумя переменными

Неравенства с двумя переменными.

Цель урока: познакомиться с определением неравенства с двумя переменными и понятием решения неравенства с двумя переменными; познакомиться со способом решения неравенств с двумя переменными ; отработать навыки решения неравенств с двумя переменными.

Определение. Неравенства вида f(х, у) > 0 или f(х, у) < 0, где f(х; у) - алгебраическое выражение, называется неравенством с двумя переменными. Например: х – 5у < 0, у² - 0,5х +16 ≥ 0, х³+(х - у)² -1>0 –

Решения неравенств с двумя переменными. Рассмотрим неравенство (х – у)(х + 2у) > 0.Пара чисел (-3; -1) при подстановке в неравенство обращает его в истинное.(-3–(-1))(-3+2·(-1)) = -2·(-5) =10 > 0 – верно.А пара чисел (5; 10,5) обращает неравенство в ложное. (5 – 10,5)(5 + 2·10,5) = -5,5·26 > 0 – ложно.Пара чисел (-3; -1) является решением данного неравенства,а пара чисел (5; 10,5) – не является решением неравенства.

Определение. Решением неравенства с двумя переменными называется упорядоченная пара чисел (х; у), которая удовлетворяет этому неравенству, т. е. при подстановке обращает неравенство в истинное.

Неравенство с двумя переменными чаще всего имеет бесконечное множество решений. Решить неравенство с двумя переменными, значит найти все его решения или доказать, что решений нет. Для решения неравенств с двумя переменными используется графический метод.

Пример №1. Построим график уравнения 2х + 3у = 0. Графиком является прямая, проходящая через точки (0; 0) и (-6; 4). Так как неравенство строгое, координаты точек графика не являются его решением, поэтому прямую строим пунктирной линией. Прямая разбила плоскость на две полуплоскости. Все решения неравенства геометрически изображены точками одной из полуплоскостей.Чтобы выбрать нужную полуплоскость, подставим координаты произвольной точки в исходное неравенство. Получаем: 2·3 + 3·1 > 0 – верно, значит все решения исходного неравенства геометрически изображены точками, расположенными в верхней полуплоскости.

Алгоритм решения неравенства с двумя переменными. 1.Построить график уравнения f(х, у) = 0 . Линия графика разбивает плоскость на несколько областей, внутри каждой из которых f(х, у) сохраняет знак.2. Выбрав произвольную точку, отобрать область (или области), в которых f(х, у) имеет знак, соответствующий знаку исходного неравенства.3. В случае, если неравенство нестрогое, линия графика включается в решение.

Решить неравенство х² - 4х + у² + 6у – 12 > 0. Выделим полный квадрат в выражении левой части неравенства:Запишем неравенство в виде:Построим график уравнения (х – 2)² + ( у + 3)² = 25.А(2; -3) – точка внутренней области.Проверка: (2 – 2)² + (-3 + 3)² >25 – ложно,значит геометрической моделью решения исходного равенства является внешняя область окружности.

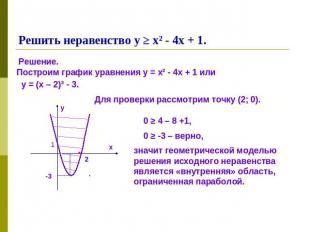
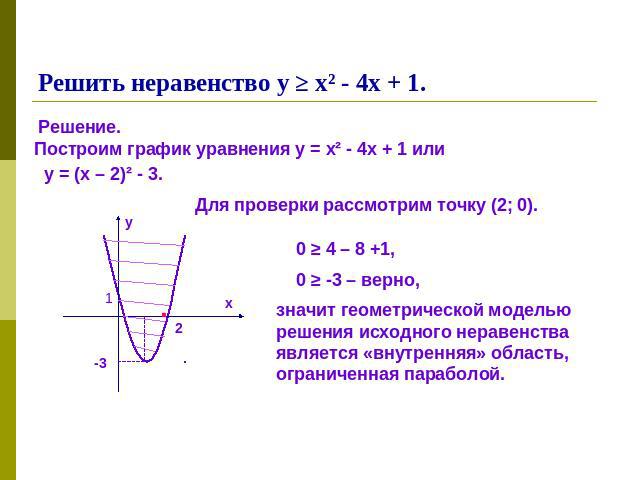
Решить неравенство у ≥ х² - 4х + 1.Решение.Построим график уравнения у = х² - 4х + 1 или Для проверки рассмотрим точку (2; 0).0 ≥ -3 – верно,значит геометрической моделью решения исходного неравенства является «внутренняя» область, ограниченная параболой.

Решить неравенство (х² + у² - 4)(х² + у² - 16) < 0. Решение.Это уравнение равносильно совокупности уравненийГрафики уравнений – окружности с центром в начале координат и радиусами 2 и 4 единичных отрезка.Так как неравенство строгое, окружности строим пунктирной линией.Окружности разбили плоскость на три области.Для проверки возмем точку средней области (3; 0).Геометрической моделью решений неравенства является средняя область.

Решить неравенства: 4х³ + 2у² - 6 < 0ху – 2 ≥ 0(х² + у ² - 1)(х² + у ² - 9) > 0

Домашнее задание. Параграф 2, п. 9, стр. 170;Решить неравенства:3sinх – у + 1 > 0;х² + у² -121 < 0;2 log5х – 2у + 3 ≥ 0.