Презентация на тему: Непрерывность функций

Непрерывность функций Лекция 3

Непрерывность Функция f(x), определенная на множестве Х, называется непрерывной в точке , если 1)она определена в этой точке, 2) существует и 3)

Условие непрерывности Существование равносильно тому, что существуют равные друг другу левосторонний и правосторонний пределы функции при , равные к тому же и значению функции в точке, то есть

Непрерывность на множестве Говорят, что функция непрерывна на множестве Х, если она непрерывна в каждой точке этого множества. Если функция непрерывна в каждой точке отрезка [a, b], то говорят, что она непрерывна на этом отрезке, причем непрерывность в точке а понимается как непрерывность справа, а непрерывность в точке b – как непрерывность слева.

Непрерывность Теперь переформулируем определение непрерывности в других терминах. Обозначим и назовем его приращением аргумента в точке , будем называть приращением функции в точке .

Непрерывность Теорема. Функция непрерывна в точке тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке, то есть если

Теоремы о непрерывных функциях Теорема. Пусть заданные на одном и том же множестве Х функции и непрерывны в точке . Тогда функции , , непрерывны в точке ,если знаменатель не равен нулю в этой точке: .

Теоремы о непрерывных функциях Теорема (о непрерывности сложной функции). Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция непрерывна в точке .

Непрерывность элементарных функций Всевозможные арифметические комбинации простейших элементарных функций, которые рассматривают в школьном курсе алгебры и начал анализа, мы будем называть элементарными функциями. Например, является элементарной. Все элементарные функции непрерывны в области определения

Разрывы функций Дадим теперь классификацию точек разрыва функций. Возможны следующие случаи. 1.Если существуют и конечны, но не равны друг другу, то точку называют точкой разрыва первого рода. При этом величину называют скачком функции в точке .

Пример Исследовать на непрерывность функцию Эта функция может претерпевать разрыв только в точке 0, где происходит переход от одного аналитического выражения к другому, а в остальных точках области определения функция непрерывна.

Решение Из условия непрерывности следует: Таким образом, в точке 0 функция претерпевает разрыв 1-го рода со скачком 1.

График функции На рисунке изображена функция, имеющая разрыв 1-го рода в начале координат.

Разрывы функций 2.Если в точке , но в точке функция либо не определена, либо , то эта точка является точкой устранимого разрыва. Последнее объясняется тем, что если в этом случае доопределить или видоизменить функцию , положив , то получится непрерывная в точке функция.

Разрывы функций 3. Точка разрыва функции, не являющаяся точкой разрыва первого рода или точкой устранимого разрыва, является точкой разрыва второго рода. Очевидно, что точки разрыва второго рода - это точки, в которых функция стремится к бесконечности. Например, в точке х=1 имеет разрыв 2-го рода.

Пример Исследуем функцию . Как элементарная функция она всюду непрерывна, кроме точки х=1. , Имеем разрыв 2-го рода с бесконечным скачком.

Первая теорема Больцано-Коши об обращении функции в нуль. Пусть функция определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения различных знаков, т. е. Тогда существует точка такая, что

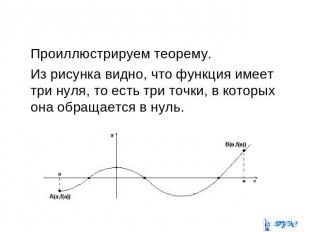
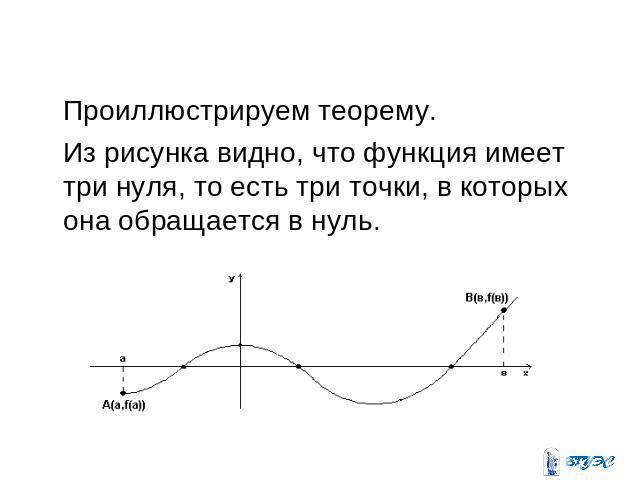
Проиллюстрируем теорему. Из рисунка видно, что функция имеет три нуля, то есть три точки, в которых она обращается в нуль.

Вторая теорема Больцано-Коши о промежуточном значении функции. Пусть функция определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает неравные значения . Тогда, каково бы ни было число между числами , найдется точка такая, что .

Теорема 1 Вейерштрасса. Если функция определена и непрерывна на отрезке [a,b], то она на этом отрезке ограничена, то есть существуют числа m и М такие, что m М для любого .

Теорема 2 Вейерштрасса. Если функция определена и непрерывна на отрезке [a,b], то она достигает на этом отрезке своих наименьшего и наибольшего значений (то есть существуют такие на отрезке [a,b], что для любого т.е. для выполняется условие .