Презентация на тему: Неравенства с двумя переменными.

познакомиться с определением неравенства с двумя переменными и понятием решения неравенства с двумя переменными; познакомиться с определением неравенства с двумя переменными и понятием решения неравенства с двумя переменными; познакомиться со способом решения неравенств с двумя переменными ; отработать навыки решения неравенств с двумя переменными.

Неравенства вида f(х, у) > 0 или f(х, у) < 0, где f(х; у) - алгебраическое выражение, называется неравенством с двумя переменными. Неравенства вида f(х, у) > 0 или f(х, у) < 0, где f(х; у) - алгебраическое выражение, называется неравенством с двумя переменными. Например: х – 5у < 0, у² - 0,5х +16 ≥ 0, х³+(х - у)² -1>0 –

Рассмотрим неравенство Рассмотрим неравенство (х – у)(х + 2у) > 0. Пара чисел (-3; -1) при подстановке в неравенство обращает его в истинное. (-3–(-1))(-3+2·(-1)) = -2·(-5) =10 > 0 – верно. А пара чисел (5; 10,5) обращает неравенство в ложное. (5 – 10,5)(5 + 2·10,5) = -5,5·26 > 0 – ложно. Пара чисел (-3; -1) является решением данного неравенства, а пара чисел (5; 10,5) – не является решением неравенства.

Решением неравенства с двумя переменными называется упорядоченная пара чисел (х; у), которая удовлетворяет этому неравенству, т. е. при подстановке обращает неравенство в истинное. Решением неравенства с двумя переменными называется упорядоченная пара чисел (х; у), которая удовлетворяет этому неравенству, т. е. при подстановке обращает неравенство в истинное.

Неравенство с двумя переменными чаще всего имеет бесконечное множество решений. Неравенство с двумя переменными чаще всего имеет бесконечное множество решений. Решить неравенство с двумя переменными, значит найти все его решения или доказать, что решений нет. Для решения неравенств с двумя переменными используется графический метод.

1.Построить график уравнения f(х, у) = 0 . 1.Построить график уравнения f(х, у) = 0 . Линия графика разбивает плоскость на несколько областей, внутри каждой из которых f(х, у) сохраняет знак. 2. Выбрав произвольную точку, отобрать область (или области), в которых f(х, у) имеет знак, соответствующий знаку исходного неравенства. 3. В случае, если неравенство нестрогое, линия графика включается в решение.

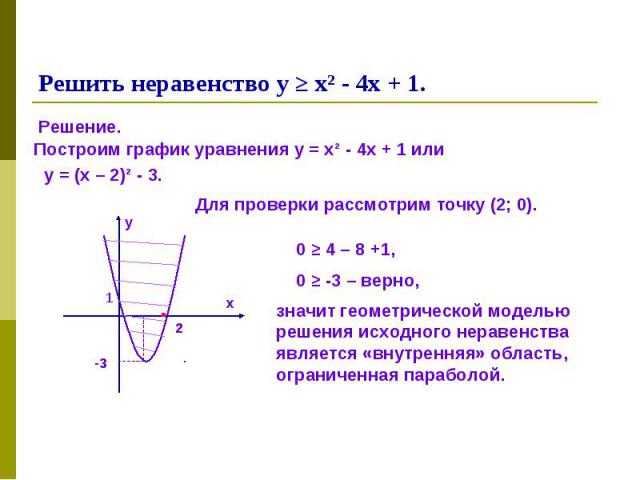
Выделим полный квадрат в выражении левой части неравенства: Выделим полный квадрат в выражении левой части неравенства:

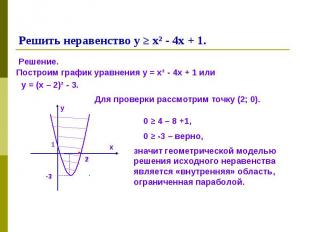
Решение. Решение.

4х³ + 2у² - 6 < 0 4х³ + 2у² - 6 < 0 ху – 2 ≥ 0 (х² + у ² - 1)(х² + у ² - 9) > 0

Параграф 2, п. 9, стр. 170; Параграф 2, п. 9, стр. 170; Решить неравенства: 3sinх – у + 1 > 0; х² + у² -121 < 0; 2 log5х – 2у + 3 ≥ 0.