Презентация на тему: Применение производной для исследования функций

Применение производной для исследования функций 1. Нахождение промежутков возрастания функции. 2. Нахождение промежутков убывания функции. 3. Нахождение промежутков постоянства функции. 4. Нахождение экстремумов. 5. Решение уравнений. 6.Нахождение наибольшего и наименьшего значения функции, непрерывной на отрезке.
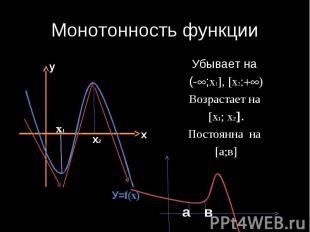
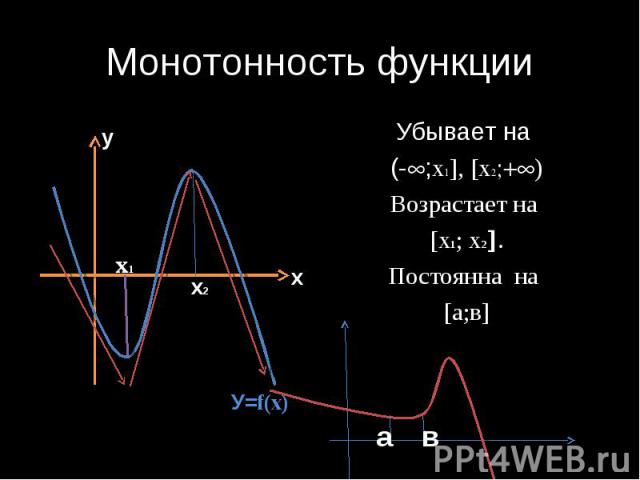
Монотонность функции Убывает на (- ;x , x ) Возрастает на х1; х2 . Постоянна на а;в
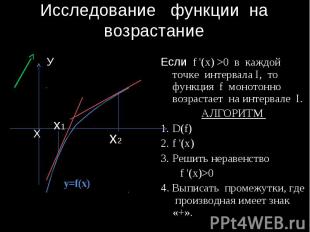
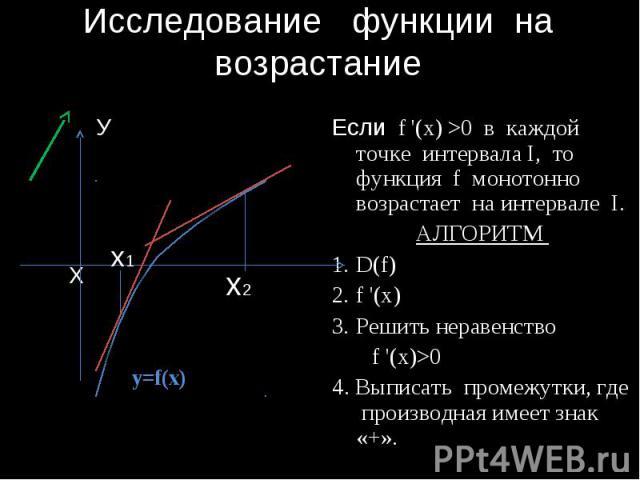
Исследование функции на возрастание Если f '(x) >0 в каждой точке интервала I, то функция f монотонно возрастает на интервале I. АЛГОРИТМ D(f) f '(x) Решить неравенство f '(x)>0 4. Выписать промежутки, где производная имеет знак «+».
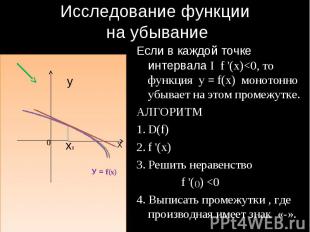
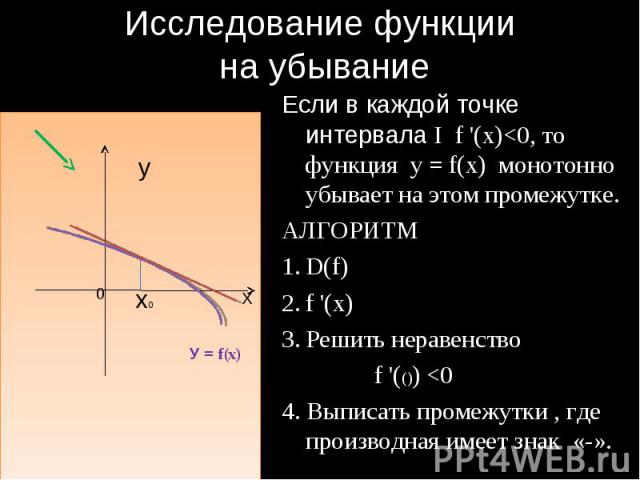
Исследование функции на убывание Если в каждой точке интервала I f '(x)
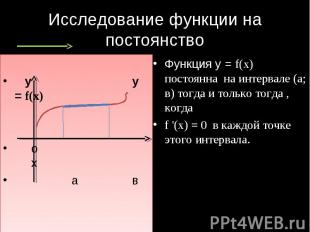
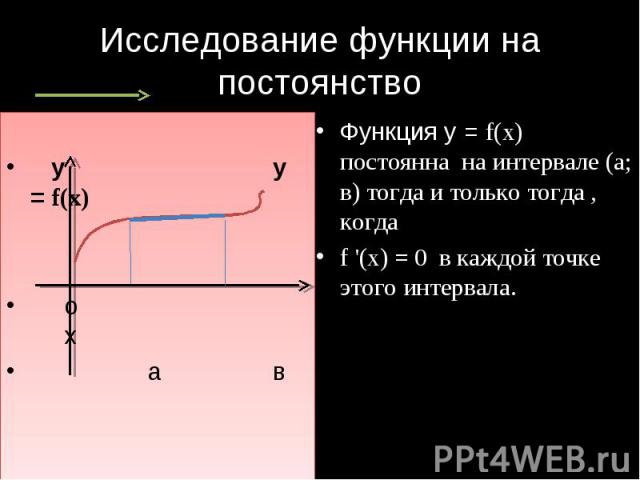
Исследование функции на постоянство Функция у = f(x) постоянна на интервале (а; в) тогда и только тогда , когда f '(x) = 0 в каждой точке этого интервала.
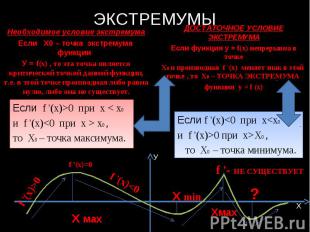
ЭКСТРЕМУМЫ Необходимое условие экстремума Если Х0 – точка экстремума функции У = f(x) , то эта точка является критической точкой данной функции, т.е. в этой точке производная либо равна нулю, либо она не существует. Если f '(x)>0 при х < x0 и f '(x) x0 , то Х0 – точка максимума. ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА Если функция у = f(x) непрерывна в точке Х0 и производная f '(x) меняет знак в этой точке , то Х0 – ТОЧКА ЭКСТРЕМУМА функции у = f (x) Если f '(x)

СХЕМА ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ ИНТЕРВАЛОВ МОНОТОННОСТИ И ЭКСТРЕМУМОВ
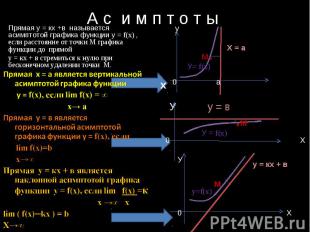
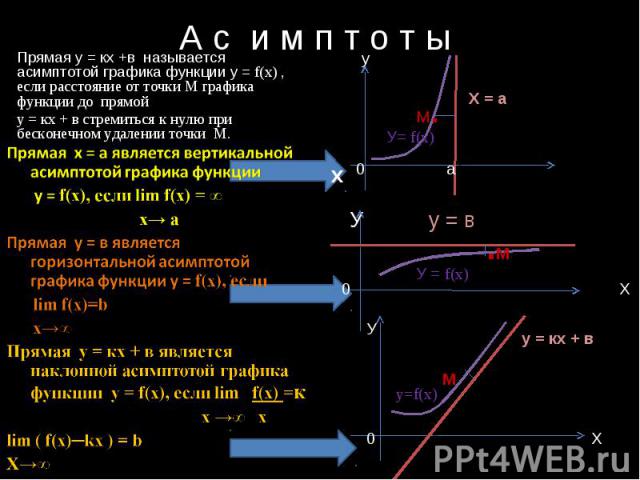
А с и м п т о т ы Прямая у = кх +в называется асимптотой графика функции у = f(x) , если расстояние от точки М графика функции до прямой у = кх + в стремиться к нулю при бесконечном удалении точки М. Прямая х = а является вертикальной асимптотой графика функции у = f(x), если lim f(x) = ∞ х→ а Прямая у = в является горизонтальной асимптотой графика функции у = f(x), если lim f(x)=b х→∞ Прямая у = кх + в является наклонной асимптотой графика функции у = f(x), если lim f(x) =к х →∞ х lim ( f(x)─kx ) = b Х→∞

СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЁ ГРАФИКА. НАХОЖДЕНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ И ОБЛАСТИ ЗНАЧЕНИЙ ФУНКЦИИ. ИССЛЕДОВАНИЕ ФУНКЦИИ НА ЧЕТНОСТЬ И НЕЧЕТНОСТЬ. ИССЛЕДОВАНИЕ ФУНКЦИИ НА ПЕРИОДИЧНОСТЬ. ОПРЕДЕЛЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГРАФИКА ФУНКЦИИ С ОСЯМИ КООРДИНАТ И ИНТЕРВАЛОВ, ГДЕ ФУНКЦИЯ СОХРАНЯЕТ ЗНАК. НАХОЖДЕНИЕ АСИМПТОТ ГРАФИКА ФУНКЦИИ. ОПРЕДЕЛЕНИЕ ТОЧЕК ЭКСТРЕМУМОВ ФУНКЦИИ. ПОСТРОЕНИЕ ГРАФИКА.
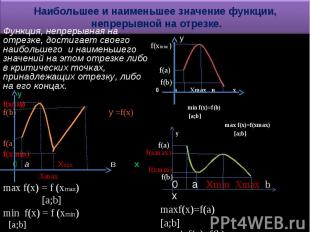
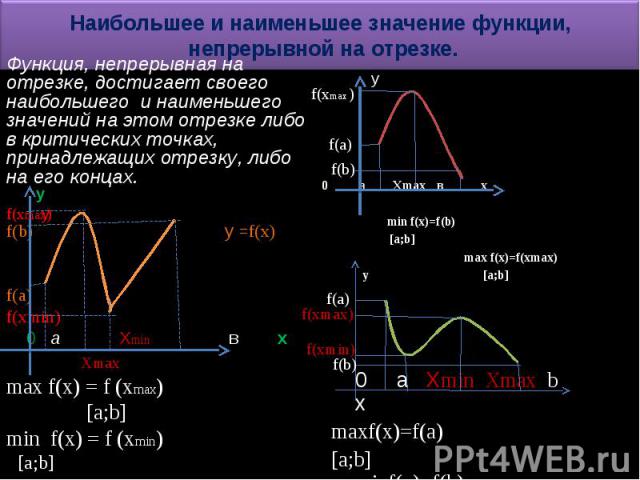
Наибольшее и наименьшее значение функции, непрерывной на отрезке. Функция, непрерывная на отрезке, достигает своего наибольшего и наименьшего значений на этом отрезке либо в критических точках, принадлежащих отрезку, либо на его концах.

۩ Схема нахождения наибольшего и наименьшего значений функции, непрерывной на отрезке ЭТАПЫ Найти производную Найти на данном отрезке критические точки, т.е. точки, в которых f’(x)=0 или не существует Вычислить значения функции в критических точках и на концах отрезка. Из вычисленных значений выбрать наименьшее и наибольшее. пример для функции у = 2x³-3x²-36x+5 на отрезке [0;4] f ' (x)=6x²-6x-36 f '(x)=0 при х = -2 и при х = 3. Отрезку [0;4] принадлежит только одна критическая точка: х = 3. 3. f (0)=5; f (3)=-76; f (4)=-59 4. max f(x)=f(0)=5; min f(x)=f(3)=-76 [0;4] [0;4]