Презентация на тему: Применение производной 11 класс

Применение производной к исследованию функций 11 класс учитель Чепаева М. И. МОУ «Пичпандинская средняя школа»

Историческая справка Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце 17 столетия. Тем более поразительно, что за долго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, но и сумел найти максимум функции f(x)= х2(а -х) В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.

Различные варианты изложения, приме- нённые к разным задачам, встречаются уже у Р. Декарта, французского математи- ка Роберваля (1602 -1675 ) английского Учёного Д.Грегори (1638 -1675), в работе И. Барроу (1630 -1677) Систематическое учение о производных развито Лейбницем и Ньютоном, который сформулировал и две основные пробле- мы анализа:

«1. Длина проходимого пути постоянно дана; требуется найти скорость движения в предложенное время пути. 2.Скорость движения постоянно дана; требуется найти длину пройденного в предложенное время пути». Первая проблема задаёт программу развития дифференциального исчисления. Вторая относится к интегральному исчислению. На первый вопрос вы знаете ответ, а на второй узнаете изучив следующую главу.

Знаешь ли эти формулы? (f(x)+g(x))| (ex ) | ( ax )| (f(x)*g(x))| (ap ) | (kx+b)| (logax)| (sin (kx +b))| (cos (kx+b))|

Выполните устно 1.Найти производную функции. а)ех+х2 б)е-3х в)е 1-х - х-3 г)2х - х-2 2.Найти угловой коэффициент касательной к графику функции у=х2-3 с абсциссой х0= 5 3.Найдите стационарные точки для функции у=2х; у=х2; у=sinx

Продолжи утверждение 1.Если производная функции положительна на промежутке, то функция … 2.Если производная функции отрицательна на промежутке, то функция … 3.Критические точки - это точки …. 4.Промежутки монотонности это …. 5.Если производная функции при переходе через стационарную точку меняет знак с «+» на «-», то…. а если с «-» на «+» то….. 6.Уравнение касательной имеет вид ….. 7.Геометрический смысл производной состоит в том, что …

верно ли ?. 1.В точке возрастания функции её производная больше нуля. 2.Если производная функции в некоторой точке равна нулю, то в этой имеется экстремум. 3.Производная произведения равна произведению производных. 4.Наибольшее и наименьшее значение функции на некотором отрезке наблюдаются или в стационарных точках, или на концах отрезка. 5.Любая точка экстремума является критической.

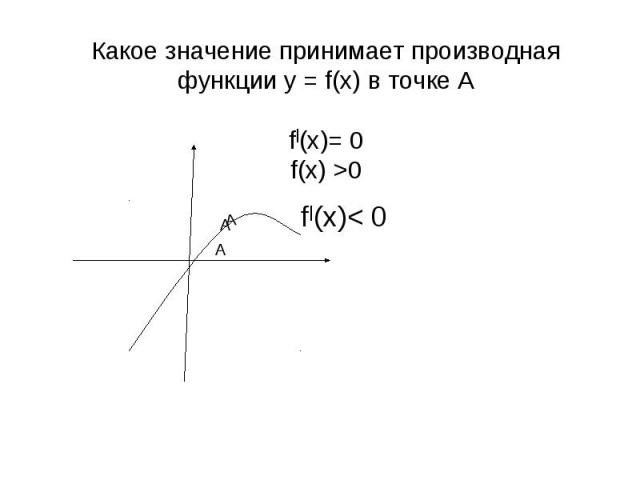
Какое значение принимает производная функции у = f(x) в точке А f|(x)= 0 f(x) >0

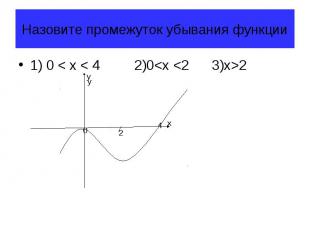
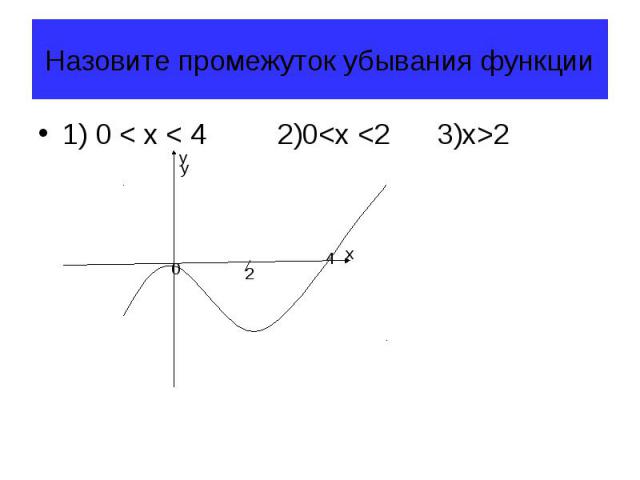
Назовите промежуток убывания функции 1) 0 < x < 4 2)0

Выполни эскиз графика функции. 1.Область определения [ -4; 3 ] 2.Множество значений [ -4; 2 ] 3.Производная положительна (-4; 1) 4.Производная отрицательна (1; 3) 5.Нули функции: -2 и 2

1.Изобрази схематически график какой либо функции, для которой: .х= -3 точка максимума, х=4 точка минимума. 2. имеет две точки максимума и одну точку минимума.

Выполни тест А1Найти производную функци у=3х4-sinх+5 1)12х3-cos х 2)4х3+cosx 3)12x3+cosx +5 А2. Какие из данных функций возрастают на всей области определения: 1)у= -3х+1; 2) у=-3х2; 3)у=х2 +1; 4)у=6х; А3.Какая из функций имеет точки экстремума: 1)у=2х; 2)у=7-5х; 3) у=х3+2х; 4)у=х2+1; А4 Дано f(x)=(3+4x)(4x-3). Найти f/(-1) 1) -32; 2) 32; 3) -50; 4)50; А5 Дано х(t)=13t2+2t+1; t=2. Найти V 1) 36; 2)57; 3)54; 4)38

Тест № 2 В1 Найдите наибольшее значение функции 2х4 -8х на отрезке [ -2; 1] В2 Найти длину промежутка убывания функции у=2х3-24х В3 Найти наименьшее значение функции f(x)=3sinx на отрезке [0,5 пи; 1,5 пи]