Презентация на тему: Предел функции в точке

Предел функции в точке

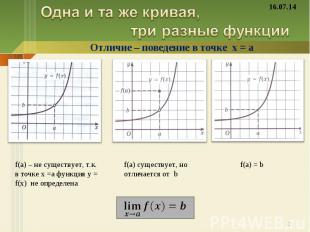
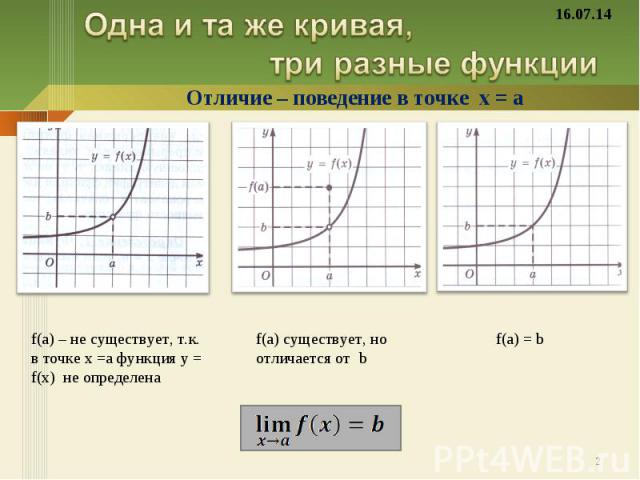
Одна и та же кривая, три разные функции f(a) – не существует, т.к. в точке х =а функция у = f(х) не определена f(a) существует, но отличается от b f(a) = b

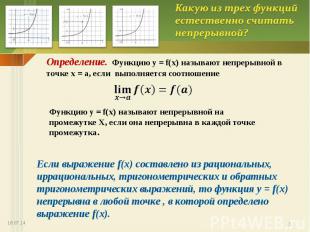
Какую из трех функций естественно считать непрерывной? Определение. Функцию у = f(х) называют непрерывной в точке х = а, если выполняется соотношение Функцию у = f(х) называют непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка. Если выражение f(х) составлено из рациональных, иррациональных, тригонометрических и обратных тригонометрических выражений, то функция у = f(х) непрерывна в любой точке , в которой определено выражение f(х).

Вычисление пределов функции Правила вычисления пределов. Если , , то Предел суммы равен сумме пределов. + = b+c 2. Предел произведения равен произведению пределов = b • c 3. Предел частного равен частному пределов (с 0) = b/c

Примеры вычисления пределов

Выполнить задания В классе: №39.23(а,б)- №39.25(а,б); № 39.29(а,б) Дома: №39.23(в,г); № 39.27(в,г); №39.29(в)

Использованная литература Мордкович А.Г., Семенов П.В. «Алгебра и начала математического анализа. Профильный уровень». 10 класс.