Презентация на тему: Применение производной к исследованию функции

Применение производной к исследованию функции

Цель занятия: ПОВТОРЕНИЕ ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ ФУНКЦИИ И ПРИМЕНЕНИЕ ПРИ ИССЛЕДОВАНИИФУНКЦИИ,ФОРМИРОВАНИЕ ПРИЕМОВ ОБОБЩЕНИЯ, РАЗВИТИЕ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ, УМЕНИЕ ПРИМЕНЯТЬ ЗНАНИЯ ПРИ ВЫПОЛНЕНИИ ПРАКТИЧЕСКОГО ЗАДАНИЯ. ВОСПИТАНИЕ ПОЛОЖИТЕЛЬНОГО ИНТЕРЕСА К ИЗУЧАЕМОМУ МАТЕРИАЛУ, АКТИВИЗАЦИИ МЫСЛИТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ, СОЗНАТЕЛЬНОЙ ДИСЦИПЛИНЫ, КУЛЬТУРЫ РЕЧИ.

ЗАДАЧА: УМЕТЬ ИССЛЕДОВАТЬ ФУНКЦИЮ С ПОМОЩЬЮ ПРОИЗВОДНОЙ , ЗНАТЬ Достаточный признак возрастания(убывания) функции,Признак максимума (минимума) функции, СФОРМИРОВАТЬ ПОНЯТИЕ ОБ АЛГОРИТМЕ, СПОСОБАХ ИССЛЕДОВАНИЯ ФУНКЦИИ ∙

Знаете ли вы, что… Исследование функций с помощью производной позволяет более точно строить их графики, которые применяются для решения многих алгебраических задач.

План работы на уроке ПовторениеИзучение нового материалаЗакреплениеПроверочная работаОбобщение изученного материалаДомашнее заданиеИтог урока

Давайте вспомним… Достаточный признак возрастания функцииДостаточный признак убывания функцииНеобходимое условие экстремумаПризнак максимума функцииПризнак минимума функции

Изучение нового материала Область определенияЧётность, нечётность; периодичностьТочки пересечения графика с осями координатПромежутки знакопостоянстваПромежутки возрастания и убыванияТочки экстремума и значения f в этих точкахПоведение функции в окрестности “особых” точек и при больших по модулю x.Упражнения

Выполните устно: Выполните устно: Для функции f(x)=х3 определить D(f), четность, возрастание, убывание.Ответ:D(f)=R, нечётная, возростающая.Докажите, что функция f(x)=х5+4х возрастает на множестве R.2) Пример исследования функции

f(x)=3x5-5x3+2 1) D(f)=R, так как f – многочлен2) f(-x)=-3x5+5x3+2, значит f(x) ни чётная, ни нечётная; не периодическая3) Пересечение с осью Оу: 3х5-5х3+2=0, отсюда х=15),6) f’(x)=15x4-15x2=15x2(x2-1) D(f)=R, поэтому критических точек, для которых f’(x) не существует, нет f’(x)=0, если х2(х2-1)=0, т.е. при х=0, х=-1, х=1Таблица, график
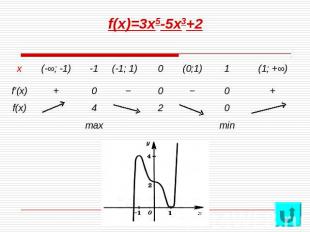
f(x)=3x5-5x3+2

Задание Используя схему исследования функции выполните задание: п. 24; №296 (а; б), №299 (а; б).

Проверочная работа: Исследовать функцию и построить её график: Вариант 1 Вариант 2f(x)=-x3+3x-2 . f(x)=x4-2x2-3 Решение Решение

Вариант 1 1) D(f)=R2) f(-x)=x3-3x-2, значит f(x) ни чётная, ни нечётная; не периодическая3) f(x)=0: (x-1)(x2+x-2)=0; x=1, x=-2; f(0)=-25),6) f’(x)=-3x2+3=-3(x-1)(x+1)Таблица, график
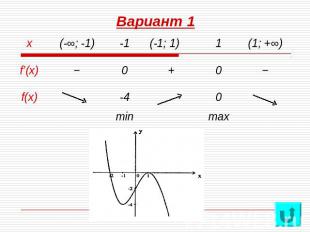
Вариант 1

Вариант 2 1) D(f)=R2) f(-x)=x4-2x2-3, значит f(-x)=f(x) для любого х, принадлежащего D(f) – функция является чётной.3) f(x)=0: (x2-3)(x2+1)=0; x=±; f(0)=-35),6) f’(x)=4х3-4x=4х(x-1)(x+1)
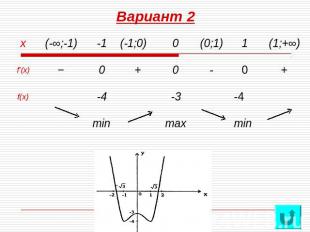
Вариант 2

Подведём итоги: Новый материал полностью усвоен, урок понравился.Тема усвоена не полностью.Ничего не было понятно.

Домашнее задание Повторить схему исследования функции. п. 24; №296 (в), №299 (в).