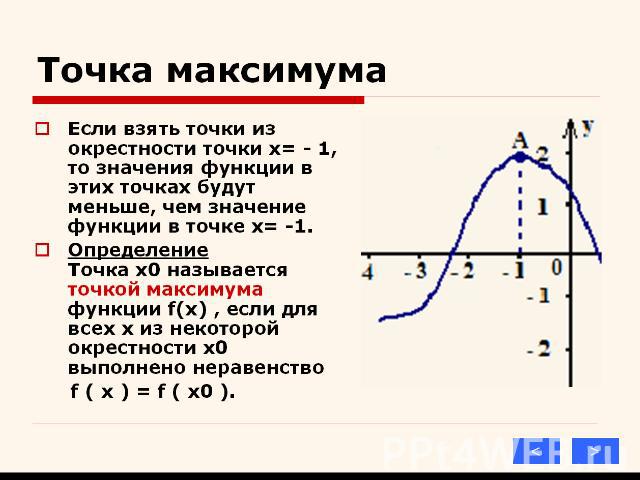
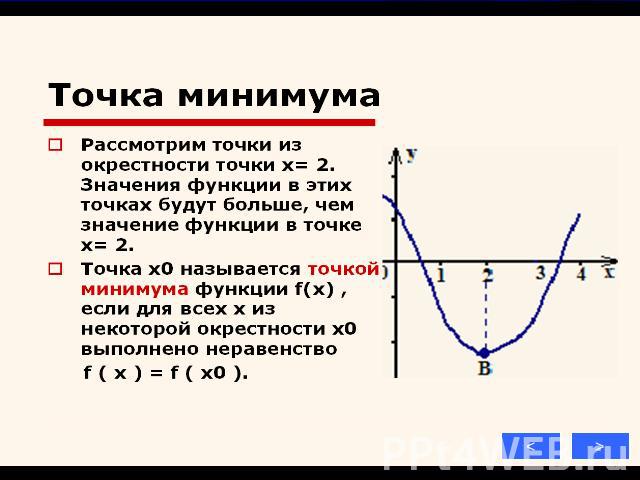
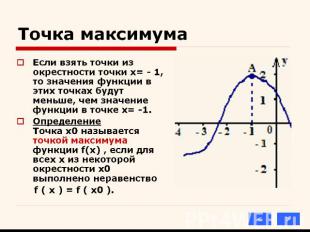
Презентация на тему: Применения производной к исследованию функции

Проект по теме :Применения производной к исследованию функции >>>Работа выполнена учениками 11Б класс МОУ Алексеевской СОШ>>>Ласковым Станиславом и Васильевым Владиславом>>>Под руководством учителя математикиПлешаковой Ольги Владимировны 2010 год

СОДЕРЖАНИЕ (можно использовать как ссылки)Из историиПонятия производнойОпределение производнойПравила дифференцирования и таблица производных Примеры применения производной к исследованию функций Точка максимумаТочка минимумаЭкстремумы функцииПримерИсточники

из истории Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач: 1) о разыскании касательной к произвольной линии 2) о разыскании скорости при произвольном законе движения Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Понятие производной Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х0 - произвольная точка этого промежутка Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) - f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x).

Определение производной

Правила дифференцирования и таблица производных

Примеры применения производной к исследованию функций Из пунктов Четные и нечетные функции,Построение графиков четных и нечетных функций и Периодические функции, что построение графика функции лучше начинать с ее исследования, которое состоит в том, что для данной функции: 1) находят ее область определения; 2) выясняют, является ли функция f четной или нечетной, является ли периодической. Далее находят: 3) точки пересечения графика с осями координат; 4) промежутки знакопостоянства; 5) промежутки возрастания и убывания; 6) точки экстремума и значения f в этих точках и 7) исследуют поведение функции в окрестности «особых» точек и при больших по модулю х. На основании такого исследования строится график функции. Исследование функции на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции f и ее критические точки, а затем выясняют, какие из них являются точками экстремума.

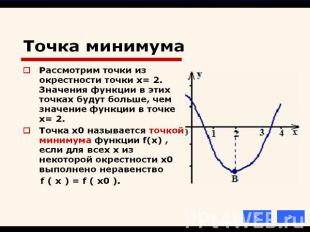
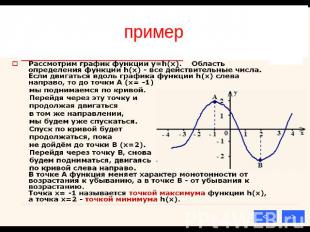
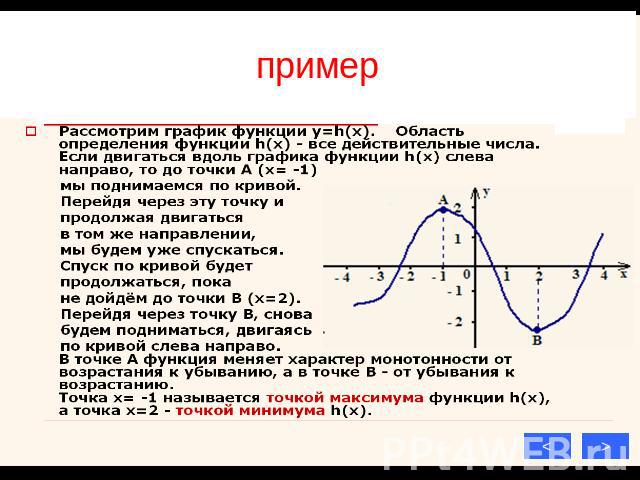
пример

источники Учебник «Алгебра и начало анализа» 10-11 класса(А.Н.Колмлгоров, А.М.Абрамов, Ю.П.Дудницын, Б.М.Ивлёв,С.И.Шварцбурд)www.sverdlovsk-school8.nm.ruhttp://www.kgafk.ru/kgufk/html/uchmat4.htmlhttp://abc.vvsu.ru/Books/u_vyssh_m1/page0030.aspИ другие…

Оцените нашу работу

Спасибо за ответ!