Презентация на тему: Биссектриса: знакомая и не очень

Биссектриса: знакомая и не очень Биссектриса – это крыса, которая бегает по углам и делит их пополам Работу выполнила ученица 8-го класса Лёвина Дарья

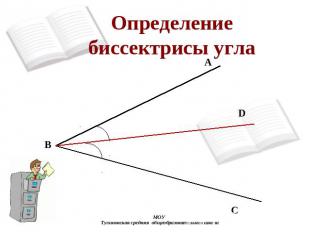
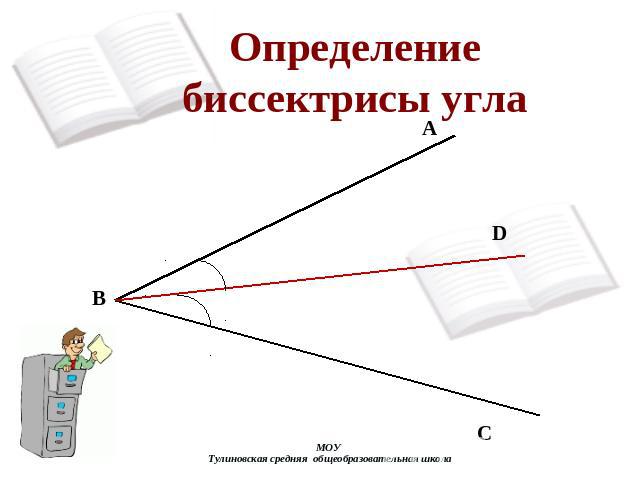
Определение биссектрисы угла

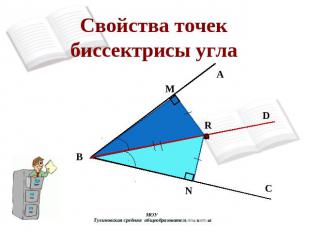
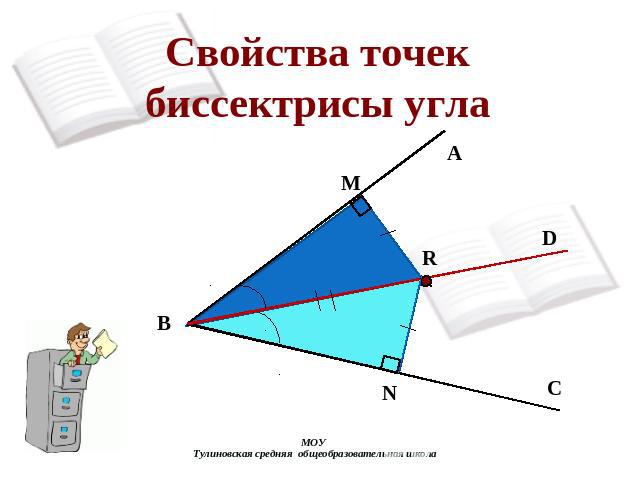
Свойства точек биссектрисы угла

Цель исследования: Определить свойство точек, равнооудаленных от сторон угла Биссектриса угла

Ход исследования 1. Изучив теоретический материал учебника и дополнительных источников информации, дать определение биссектрисы угла, биссектрисы треугольника.2. Выяснить, каким свойством обладает точка пересечения биссектрис углов треугольника.3. Рассмотреть и решить задачи по данной теме.4. Оформить результаты, сделать соответствующие выводы.

Гипотеза Существуют точки, не принадлежащие биссектрисе угла, а всё-таки равноудалённые от сторон угла

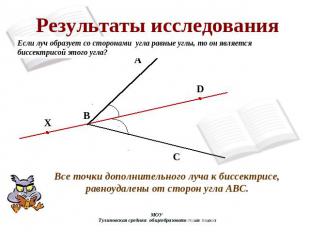
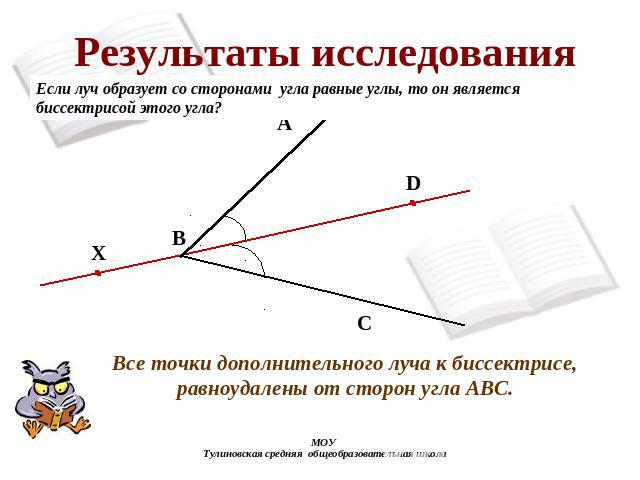
Результаты исследования Если луч образует со сторонами угла равные углы, то он является биссектрисой этого угла? Все точки дополнительного луча к биссектрисе, равноудалены от сторон угла АВС.

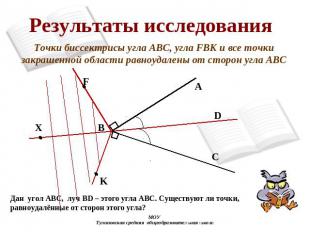
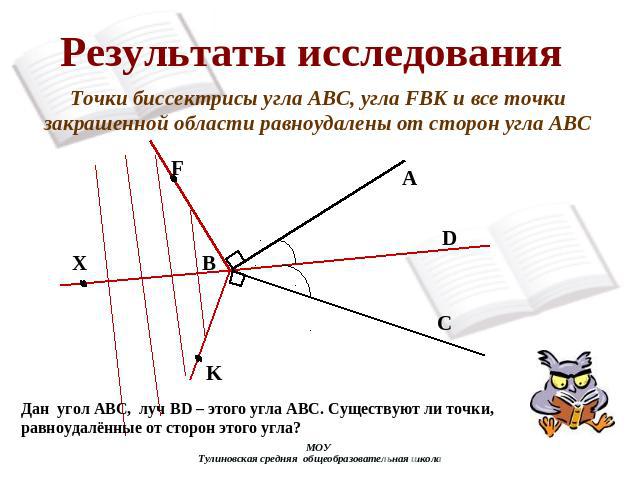
Результаты исследования Точки биссектрисы угла АВС, угла FBK и все точки закрашенной области равноудалены от сторон угла АВС Дан угол АВС, луч BD – этого угла ABC. Существуют ли точки, равноудалённые от сторон этого угла?

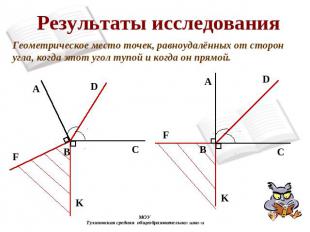
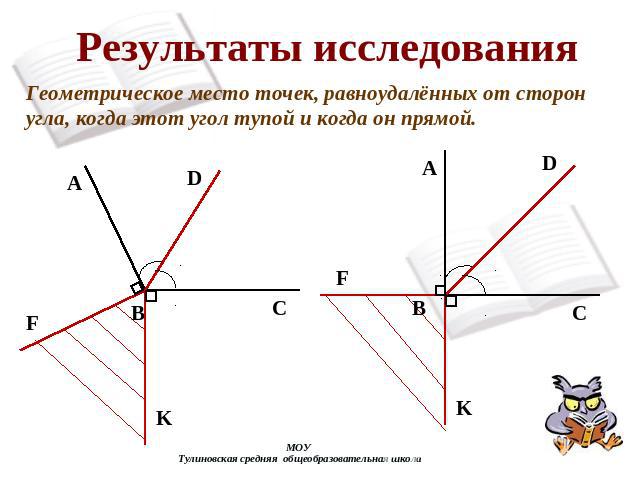
Результаты исследования Геометрическое место точек, равноудалённых от сторон угла, когда этот угол тупой и когда он прямой.

Результаты исследования Дан прямой угол АВС и круг с центром В. Найдите точки круга, которые равноудалены от сторон угла АВС. Получили фигуру, состоящую из отрезка ВЕ, равного радиусу окружности, и четверти круга - FBK

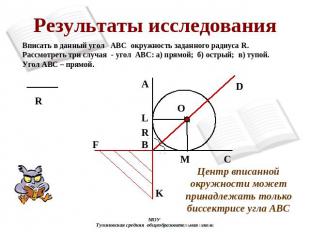
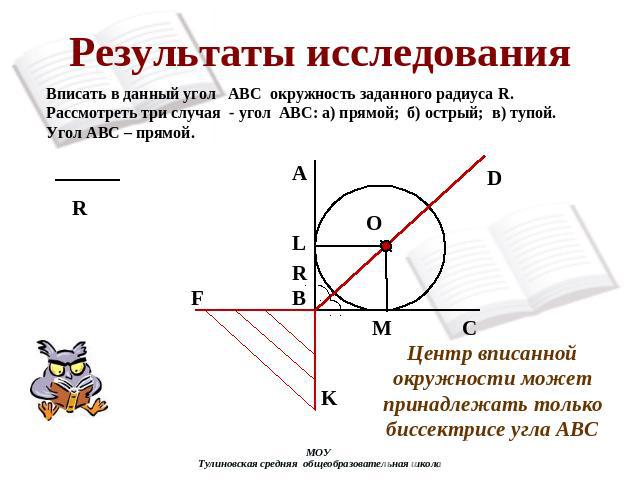
Результаты исследования Вписать в данный угол АВС окружность заданного радиуса R. Рассмотреть три случая - угол АВС: а) прямой; б) острый; в) тупой.Угол АВС – прямой. Центр вписанной окружности может принадлежать только биссектрисе угла АВС

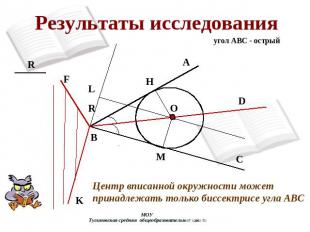
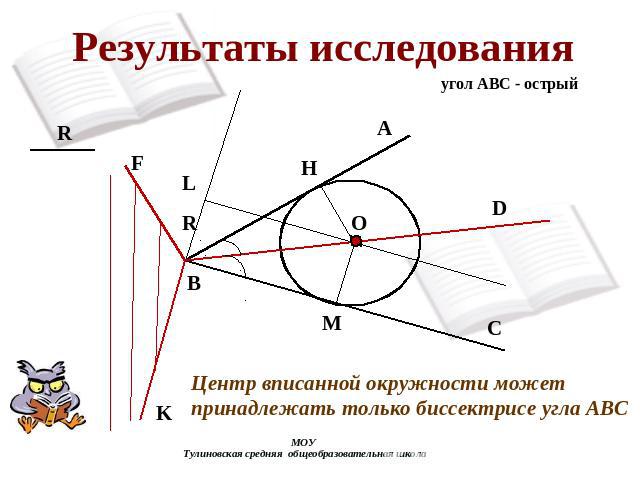
Результаты исследования угол АВС - острый Центр вписанной окружности может принадлежать только биссектрисе угла АВС

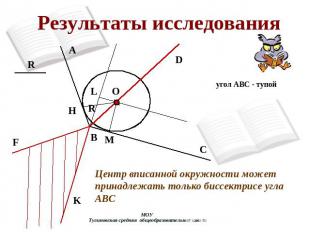
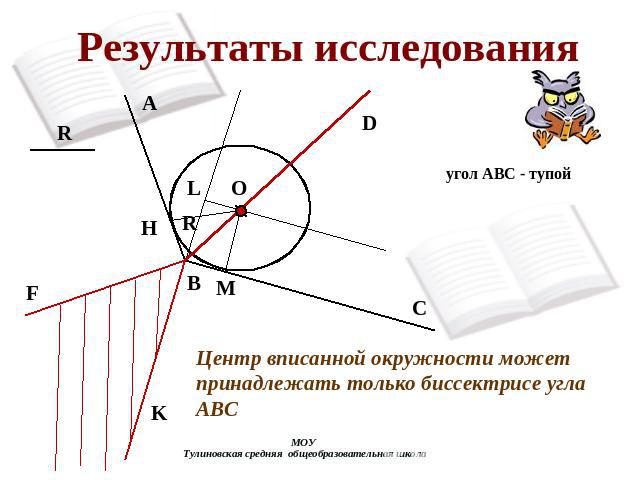
Результаты исследования Центр вписанной окружности может принадлежать только биссектрисе угла АВС

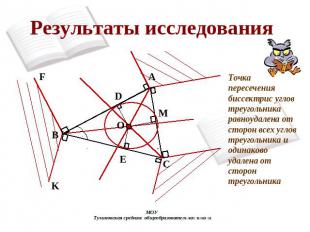
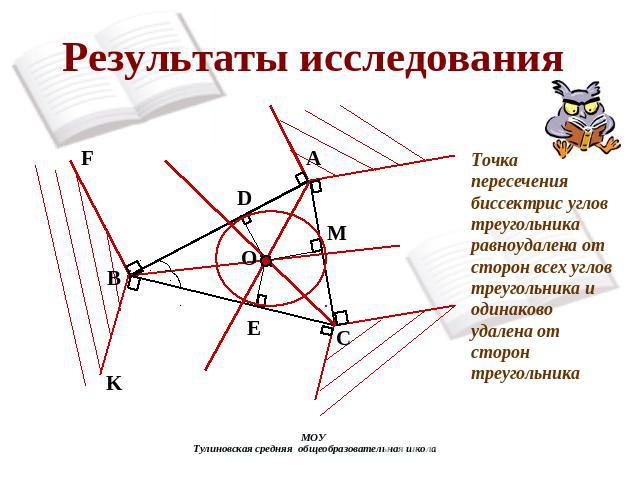
Результаты исследования Точка пересечения биссектрис углов треугольника равноудалена от сторон всех углов треугольника и одинаково удалена от сторон треугольника

Вывод Существуют точки, не принадлежащие биссектрисе угла, но всё-таки равноудалённые от сторон данного угла.Центр окружности, вписанной в угол, принадлежит только биссектрисе данного угла. Точка пересечения биссектрис углов треугольника является единственной точкой равноудаленной от сторон всех углов треугольника и от сторон треугольника.

Литература А. Атанасян., Геометрия 7-9.Никольская И. Л., Семёнов Е.Е. Учимся рассуждать и доказывать: КН. Для учащихся 6-10 кл. –М. : Просвещение, 1989.