Презентация на тему: Алгебраические дроби

Алгебраические дроби Иркутская область,г. Усолье - Сибирское,МОУ «Гимназия №9»Ученица 8 класса «А»Гилёва ЯнаУчитель: Сизых Татьяна Валентиновна

Содержание 1Что такое алгебраическая дробь? Основные понятия.2Все действия с алгебраическими дробями.3Задания для самостоятельной работы.

Что такое алгебраическая дробь? Запись , в которой а – число или выражение, а b – выражение с переменной, называется рациональной (алгебраической) дробью. Пример:

Основное свойство алгебраической дроби – числитель и знаменатель алгебраической дроби можно умножать (делить) на одно и то же число, не равное нулю.

Допустимые значения переменных (ОДЗ) – такие значения переменных, при которых выражение имеет смысл (т. е. знаменатель не равен нулю).Пример 1: , Допустимые значения переменной y:

Пример 2:Допустимые значения переменной а: Пример 3:Допустимые значения переменной х:

Задание. Укажите область допустимых значений переменной:

Все действия с алгебраическими дробями Сокращение дробейУмножениеПреобразование выраженийСложение и вычитание с одинаковыми знаменателямиВозведение в степень

Сокращение дробей Чтобы сократить дробь, необходимо числитель и знаменатель данной дроби разложить на множители и сократить на общий множитель.Пример 1:

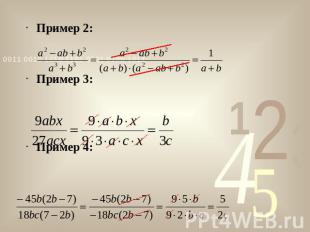
Пример 2:Пример 3:Пример 4:

Задание.Сократите дробь:

Сложение и вычитание дробей с одинаковыми знаменателями Чтобы сложить (вычесть) дроби с одинаковыми знаменателями, нужно знаменатели оставить без изменения, а числители сложить (вычесть).Примеры:

Выполните действия:

Сложение и вычитание дробей с разными знаменателями Чтобы сложить (вычесть) дроби с разными знаменателями, нужно:Разложить знаменатели дробей на множители;Привести дроби к общему знаменателю;Сложить (вычесть) числители, а знаменатели оставить без изменения.

Примеры:

Выполните действия:

Умножение дробей Произведение двух дробей равно дроби, числитель которой равен произведению числителей этих дробей, а знаменатель – произведению знаменателей.

Пример 2: Пример 3: Пример 4:

Выполните умножение:

Деление дробей Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.

Пример 2: Пример 3:

Выполните действия:

Возведение дроби в степень Чтобы возвести дробь в степень n, нужно возвести и числитель, и знаменатель в степень n.

Возведите дроби в степень:

Преобразование выражений

Решите самостоятельно:

Самостоятельная работа Упростить выражение: Результат упрощения выражения

Упростить выражение: Возвести в степень: Выполните действия:

Выполните действия: Упростить выражение:

Выполнить действия: