Презентация на тему: Алгебраические дроби Основное свойство дроби Сокращение дробей

Алгебраические дроби Основное свойство дроби Сокращение дробей

Да, помню! Но сегодня мы познакомимся с другими дробями. «In die bruche kommen» (нем., буквально: «попасть в дроби» Мишка! Ты это о чем? Куда попасть? Зачем попасть? Мишка! А мы же уже изучали дроби! Помнишь?

Я эту дробь знаю!
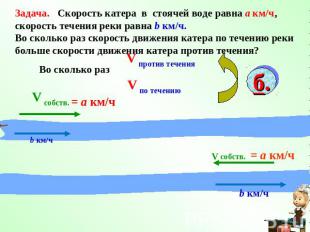
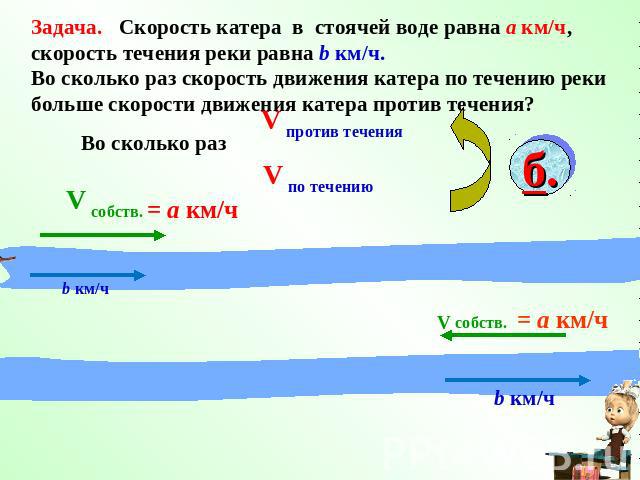
Задача. Скорость катера в стоячей воде равна а км/ч, скорость течения реки равна b км/ч.Во сколько раз скорость движения катера по течению рекибольше скорости движения катера против течения? Во сколько раз

Решение. Скорость катера по течению равна (a + b) км/ч Скорость катера против течения равна (a – b) км/чСкорость катера по течению в раз больше, чем против течения.Выражение называют алгебраической дробью; (a + b) - числитель дроби, (a – b) - знаменатель дроби.

Примеры алгебраических дробей Если вместо букв, входящих в алгебраическую дробь, подставить некоторые числа, то получится значение этой алгебраической дроби. при a = 12, b = 4

Буквы могут принимать лишь допустимые значения, т. е. такие значения, при которых знаменатель этой дроби не равен нулю. Для дроби допустимыми являются все значения а, кроме а = 0 и а = 1. Найти допустимые значения букв, входящих в дробь:

Найти допустимые значения букв, входящих в дробь: любое действительное число

Основное свойство дроби При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же число, не равное нулю, получается равная ей дробь Основное свойство дроби можно записать так: b ≠ 0, m ≠ 0, тогда Можно сокращать алгебраическую дробь на общий множитель числителя и знаменателя дроби Я же это знаю! Это сокращение дроби!

Разложите на множители:

Найдите ошибки: Мишка, Мишка!Помоги мне ошибки найти!

Сократите дроби:

Сократите дроби:

Давай спросим ребят! Мишка, Мишка!Расскажи, расскажи!Что ты знаешь об этих алгебраических дробях?

А правда, что выражение вида называют алгебраической дробью. Основное свойство дроби можно записать так: , где b≠0, m≠0 В алгебраической дроби числитель и знаменатель- алгебраические выражения. Допустимыми значениями букв, входящих в алгебраическую дробь называют такие значения, при которых числитель этой дроби не равен нулю Одним из способов разложения многочленов на множители является применение формул сокращенного умножения

Восстановите, частично стёртые записи: Ой-ой-ой…

К каждой дроби найти равную ей дробь, используя соответствие число - буква

К каждой дроби найти равную ей дробь, используя соответствие число - буква
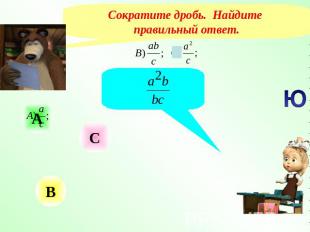
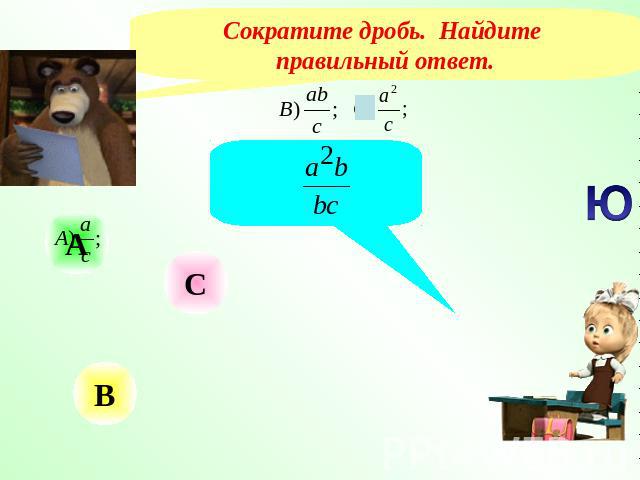
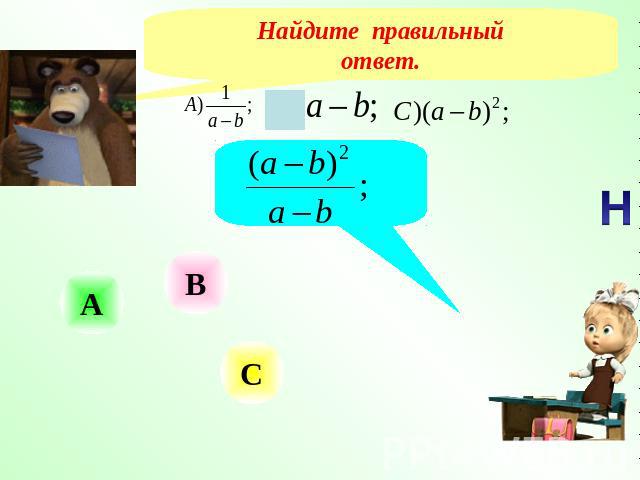
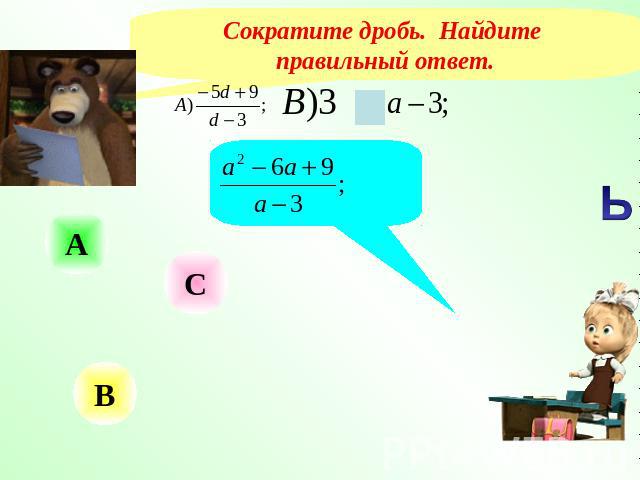
Сократите дробь. Найдите правильный ответ.
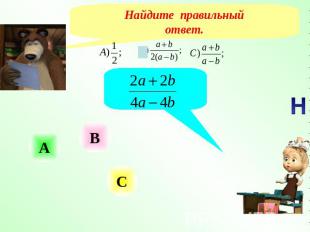
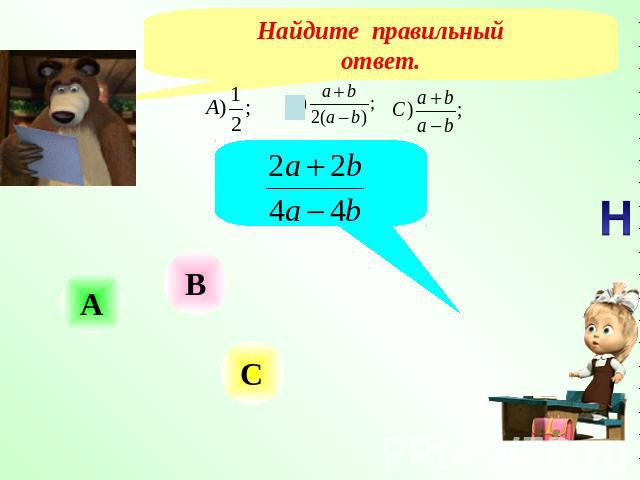
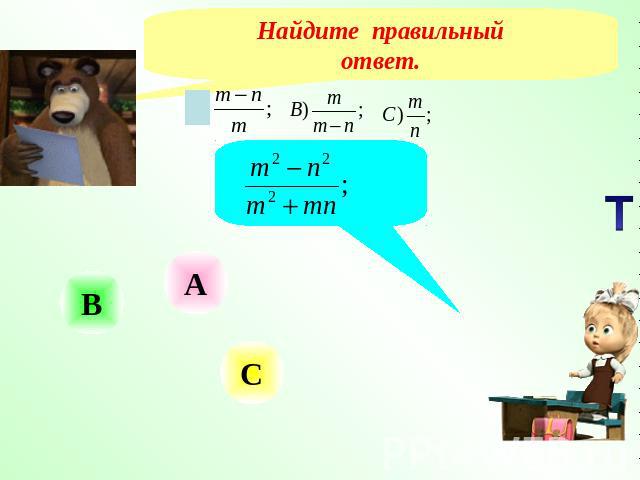
Найдите правильныйответ.
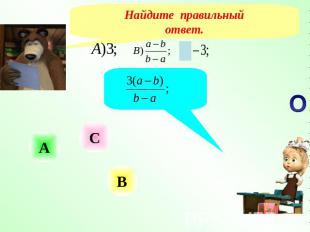
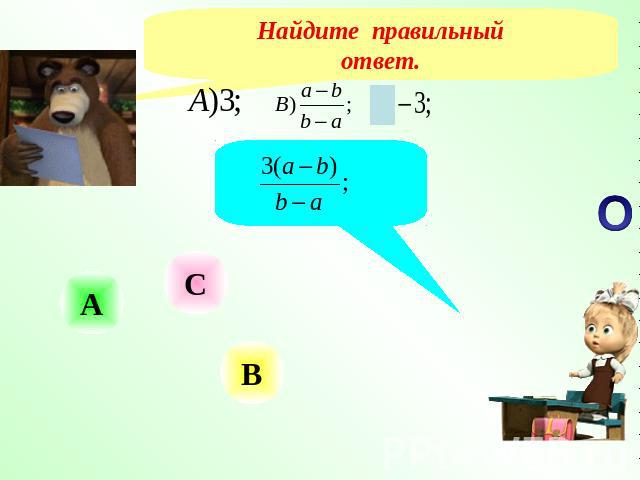
Найдите правильныйответ.
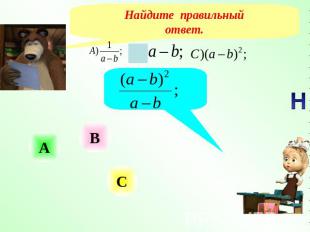
Найдите правильныйответ.
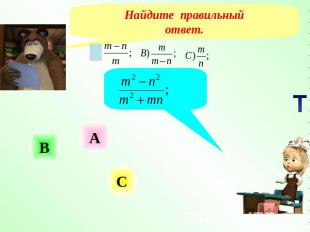
Найдите правильныйответ.
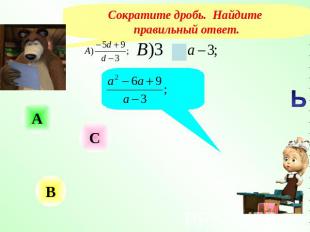
Сократите дробь. Найдите правильный ответ.

Сэр Исаак Ньютон - родился 4 января 1643 года в деревне Вулсторп (графство Линкольншир), Англия. Великий английский физик, математик и астроном. Автор фундаментального труда «Математические начала натуральной философии», в котором он описал закон всемирного тяготения и так называемые Законы Ньютона, заложившие основы классической механики. Разработал дифференциальное и интегральное исчисление, теорию цветности и многие другие математические и физические теории.

Если знаешь ты ответ, - смело потянись.Посмотри налево ты, - соседу улыбнись.Если же ответа нет, руки ты потри,И соседа справа ты о помощи проси! 1.Приведите дробь к знаменателю, равному: б)16ха) 12 в)24ab 2.Найдите допустимые значения букв:а)

Найдите значение алгебраической дроби, предварительно сократив ее: при х=10, х=0, х=5, х=2.Всегда ли это возможно?Когда нет?

Итоги урока Ой, сколько я всего узнала… Спасибо, ребята!Вы мне очень помогли!

Домашнее задание Составьте 5 дробей,которые можно сократить.Предложите соседу свое задание