Презентация на тему: Графики функций у=ах²+n и у=а(х-m)²

Графики функций у=ах²+n и у=а(х-m)²

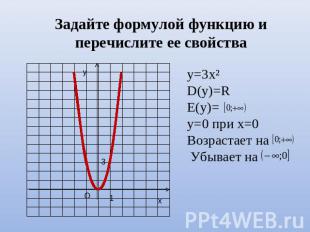
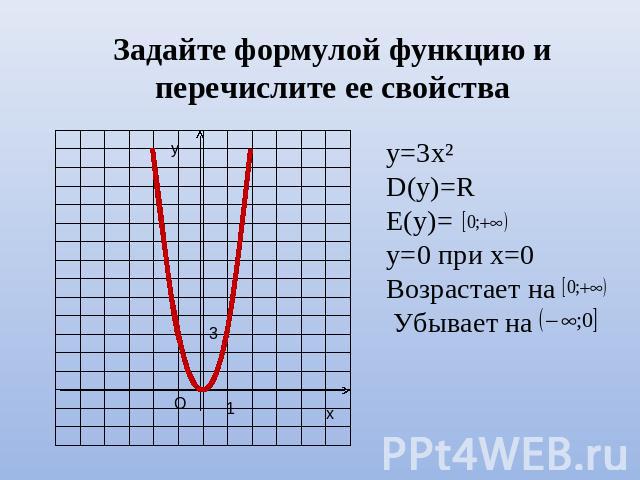
Задайте формулой функцию и перечислите ее свойства у=3х²D(y)=RE(y)=у=0 при х=0Возрастает на Убывает на

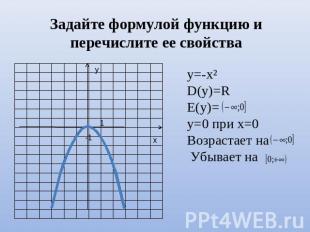
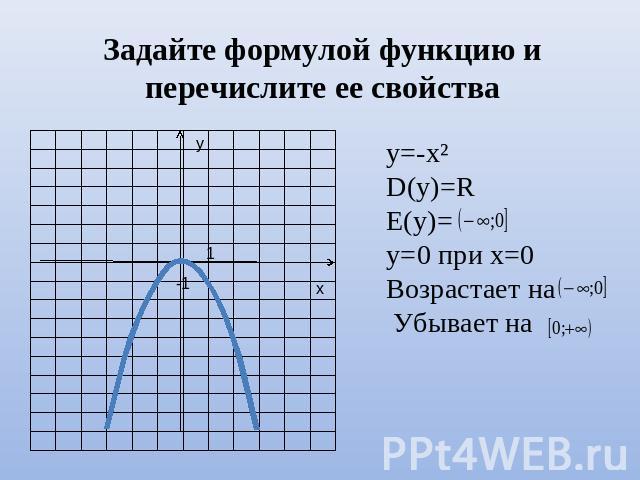
Задайте формулой функцию и перечислите ее свойства у=-х²D(y)=RE(y)= у=0 при х=0Возрастает на Убывает на

Итоги прошлого урока: График функции у=-f(x) получается из графика функции у=f(x) с помощью симметрии относительно оси абсцисс.2. График функции у=аf(x) получается из графика функции у=f(x) растяжением вдоль оси ординат в а раз при а>1 и сжатием в раз при 0<а<1.

Сравним значения функций у=2х² и у=2х²+1

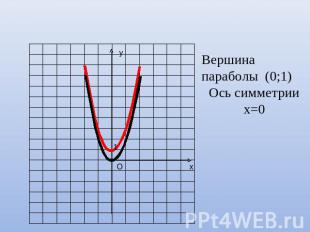
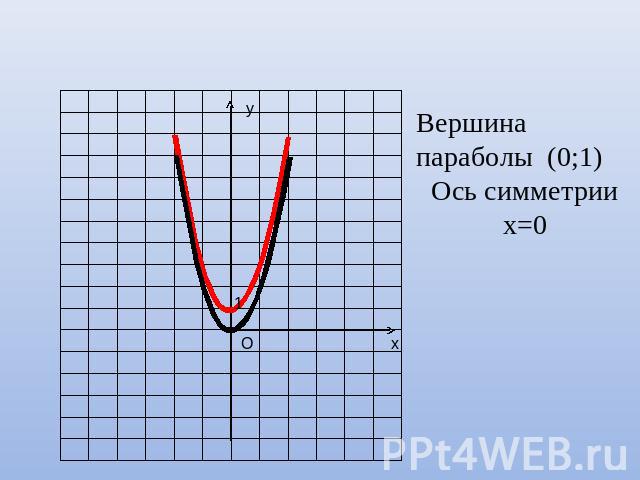
Вершина параболы (0;1)Ось симметрии х=0

График функции у=f(x)+n можно получить из графика функции у=f(x) с помощью параллельного переноса вдоль оси ординат на |n| единиц: вверх при n>0 и вниз при n<0.

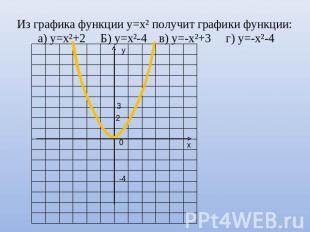
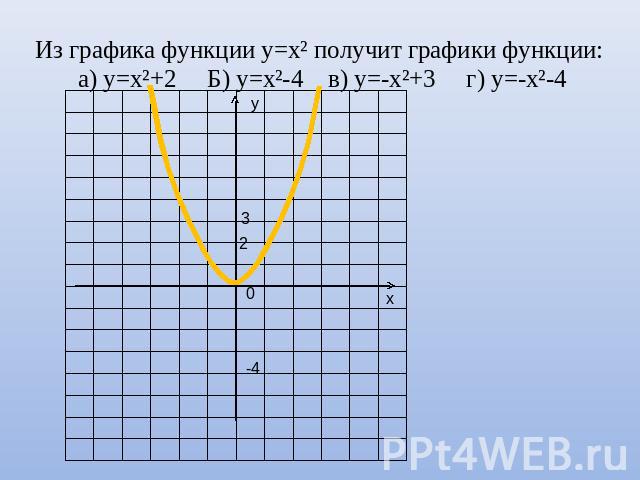
Из графика функции у=х² получит графики функции: а) у=х²+2 Б) у=х²-4 в) у=-х²+3 г) у=-х²-4

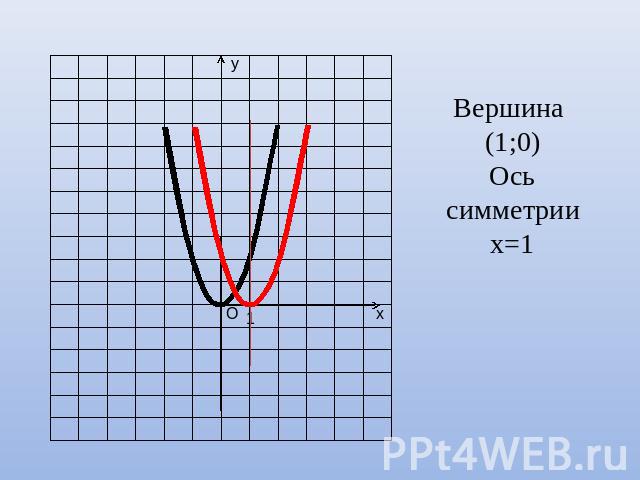
Сравним значения функций у=2х² и у=2(х-1)²

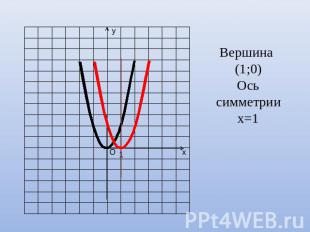
Вершина (1;0)Ось симметрии х=1

График функции у=f(x-m) получается из графика функции у=f(x) с помощью параллельного переноса вдоль оси абсцисс на |m| единиц: вправо, если m>0 и влево, если m<0.

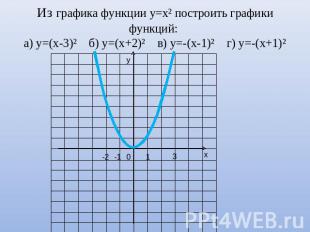
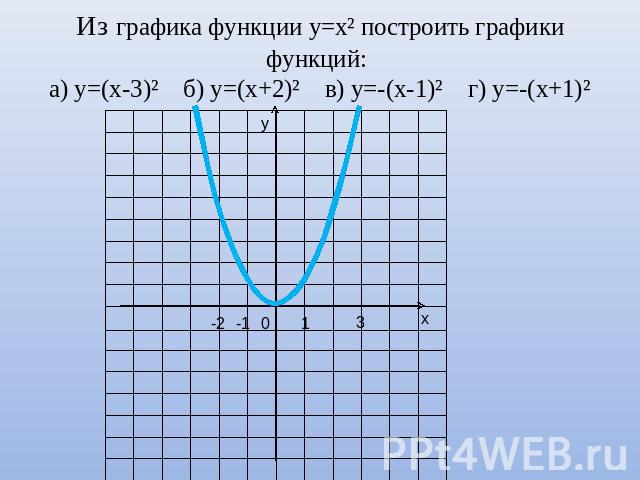
Из графика функции у=х² построить графики функций: а) у=(х-3)² б) у=(х+2)² в) у=-(х-1)² г) у=-(х+1)²

График функции у=f(x-m)+n можно получить из графика функции у=f(x) с помощью двух параллельных переносов: сдвига вдоль оси абсцисс на |m| единиц: вправо при m>0 и влево при m<0 и сдвига вдоль оси ординат на |n| единиц: вверх при n>0 и вниз при n<0.

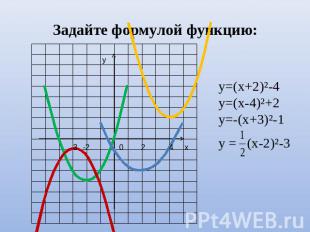
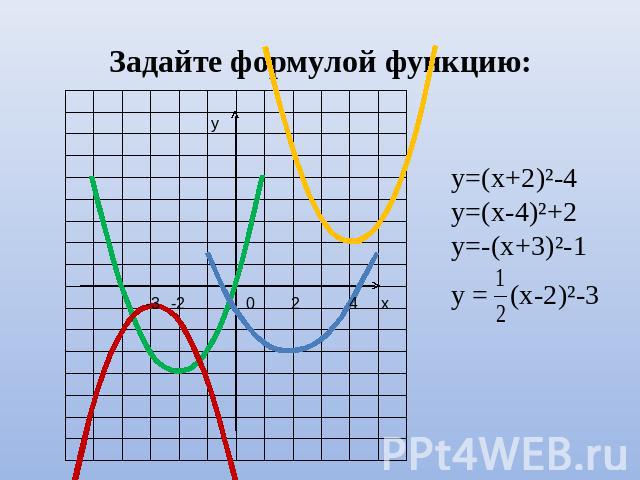
Задайте формулой функцию: у=(х+2)²-4у=(х-4)²+2у=-(х+3)²-1у = (х-2)²-3

Домашнее задание: П. 5 № 106, 107, 116.