Презентация на тему: Свойства и графики элементарных функций

Федеральное агентство по образованию.Государственное образовательное учреждениеСреднего профессионального образования.Димитровградский технический колледж. ПроектВерещука Станислава. Тема: «Свойства и графики элементарных функций». Руководитель: преподаватель Кузьмина В.В. Димитровград 2007 

Содержание: 1. Определение функции.2. Линейная функция: возрастающая; убывающая; частные случаи.3. Квадратичная функция.4. Степенная функция: с четным натуральным показателем; с нечетным натуральным показателем; с целым отрицательным показателем; с действительным показателем.5. Список использованной литературы.

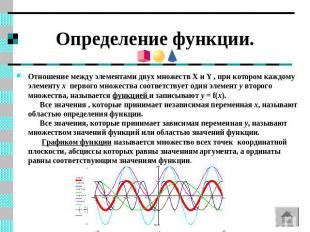
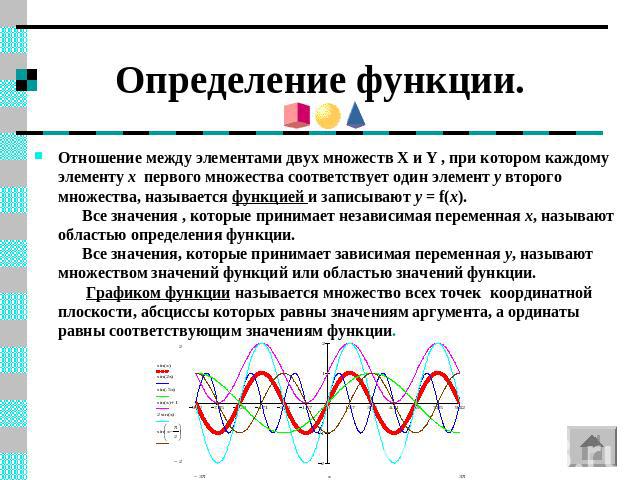
Определение функции. Отношение между элементами двух множеств X и Y , при котором каждому элементу x первого множества соответствует один элемент у второго множества, называется функцией и записывают у = f(x). Все значения , которые принимает независимая переменная x, называют областью определения функции. Все значения, которые принимает зависимая переменная y, называют множеством значений функций или областью значений функции. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты равны соответствующим значениям функции.

Линейная функция. Функция, заданная формулой y=kx+b, где k и b- некоторые действительные числа называется линейной.

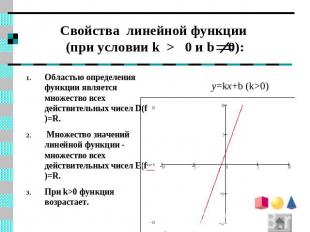
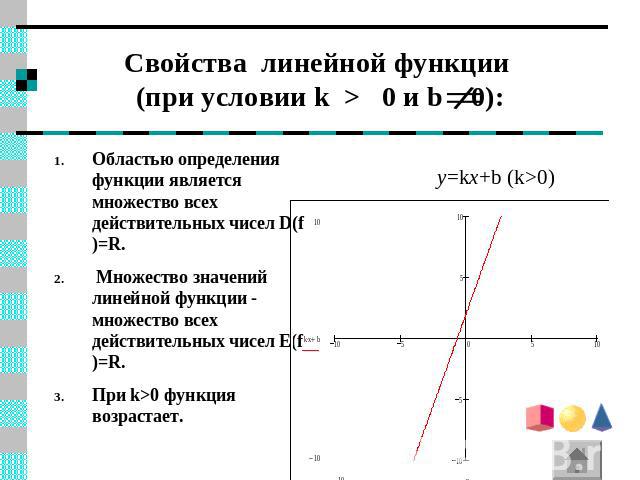
Свойства линейной функции (при условии k > 0 и b 0): y=kx+b (k>0) Областью определения функции является множество всех действительных чисел D(f)=R. Множество значений линейной функции - множество всех действительных чисел E(f)=R. При k>0 функция возрастает.

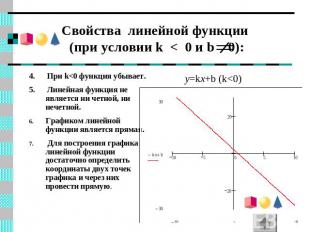
Свойства линейной функции (при условии k < 0 и b 0): y=kx+b (k<0) 4. При k<0 функция убывает.5. Линейная функция не является ни четной, ни нечетной. Графиком линейной функции является прямая. Для построения графика линейной функции достаточно определить координаты двух точек графика и через них провести прямую.

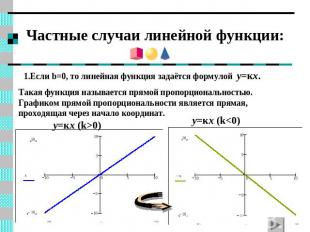
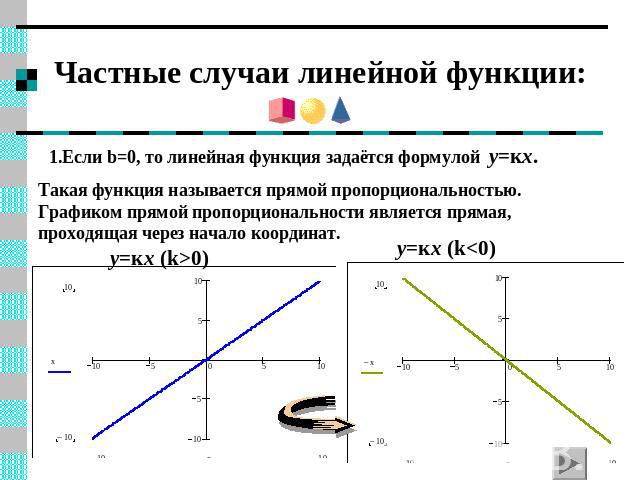
Частные случаи линейной функции: 1.Если b=0, то линейная функция задаётся формулой y=кx.Такая функция называется прямой пропорциональностью. Графиком прямой пропорциональности является прямая, проходящая через начало координат.

Частные случаи линейной функции: 2.Если k=0, то линейная функция задаётся формулой y=b. Такая функция называется постоянной. Графиком постоянной функции является прямая, параллельная оси Ох. Если k=0 u b=0, то график постоянной функции совпадает с осью Ох.

Квадратичная функция. Функция, задаваемая формулой y=ax2+bx+c - называется квадратичной, где x-независимая переменная, a b,c- некоторые числа, причем a не равняется 0.

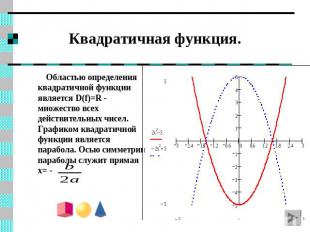
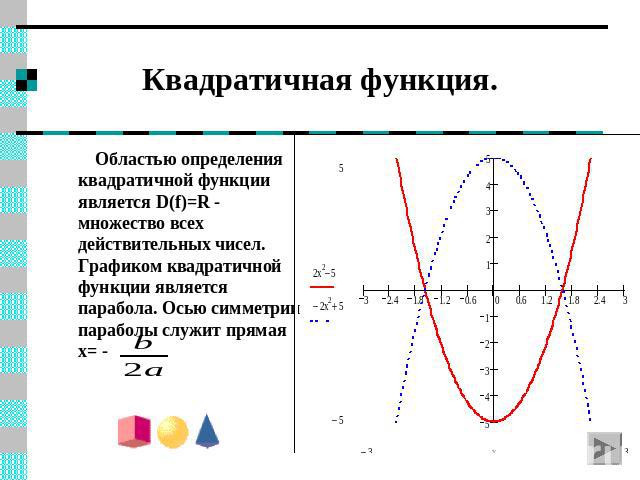
Квадратичная функция. Областью определения квадратичной функции является D(f)=R - множество всех действительных чисел. Графиком квадратичной функции является парабола. Осью симметрии параболы служит прямая x= -

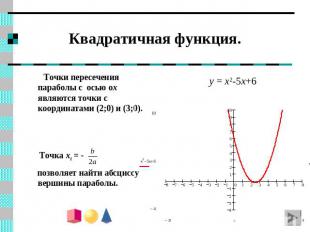
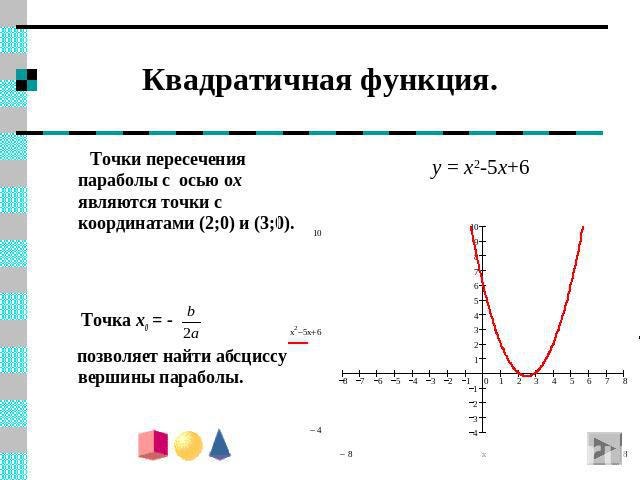
Квадратичная функция. y = x2-5x+6 Точки пересечения параболы с осью ox являются точки с координатами (2;0) и (3;0). Точка x0 = - позволяет найти абсциссу вершины параболы.

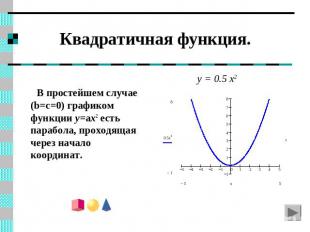
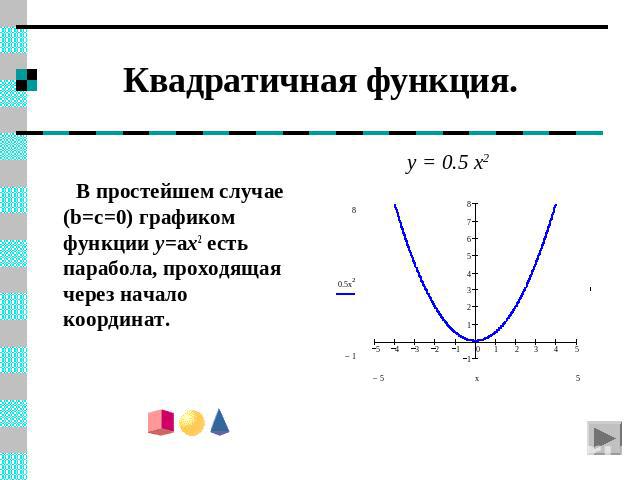
Квадратичная функция. y = 0.5 x2 В простейшем случае (b=c=0) графиком функции y=ax2 есть парабола, проходящая через начало координат.

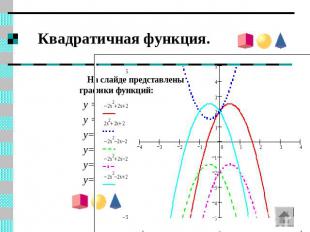
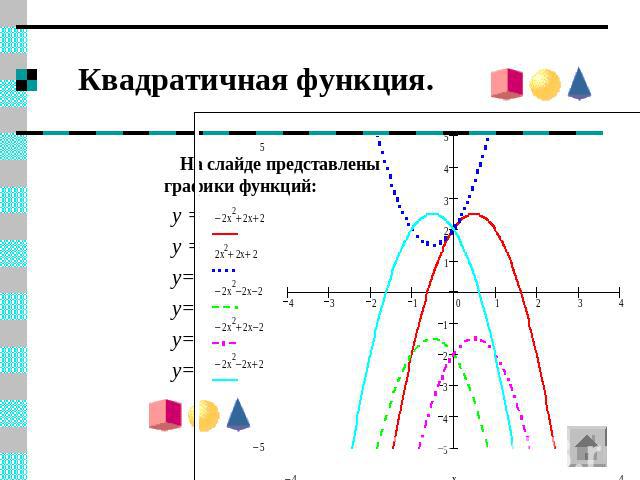
Квадратичная функция. На слайде представлены графики функций: y = y = y= y= y= y=

Степенная функция. Функция, заданная формулойy=xn, где n- натуральное число,называется степенной функцией с натуральным показателем.

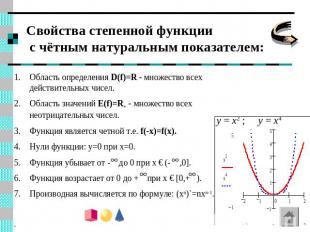
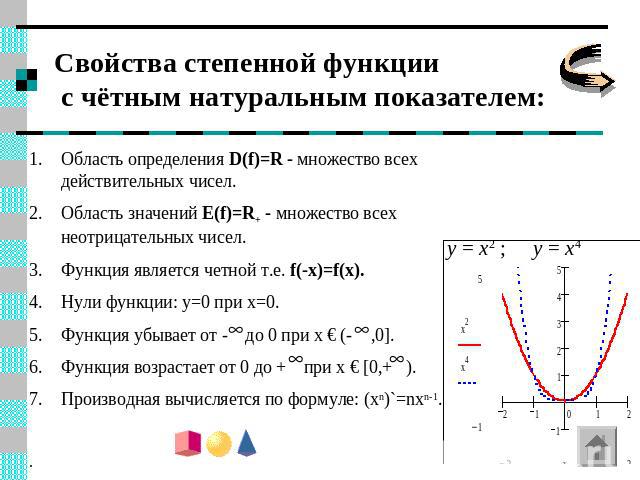
Свойства степенной функции с чётным натуральным показателем: Область определения D(f)=R - множество всех действительных чисел.Область значений E(f)=R+ - множество всех неотрицательных чисел.Функция является четной т.е. f(-x)=f(x).Нули функции: y=0 при x=0.Функция убывает от - до 0 при х € (- ,0].Функция возрастает от 0 до + при х € [0,+ ).Производная вычисляется по формуле: (xn)`=nxn-1..

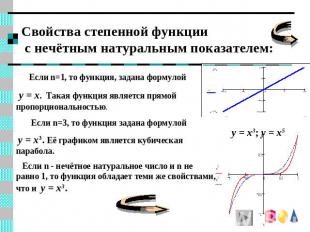
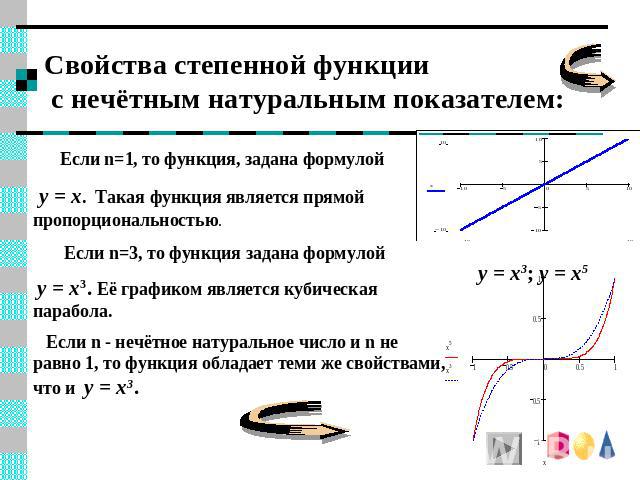
Свойства степенной функции с нечётным натуральным показателем: Если n=1, то функция, задана формулой y = x. Такая функция является прямой пропорциональностью. Если n=3, то функция задана формулой y = x3. Её графиком является кубическая парабола. Если n - нечётное натуральное число и n не равно 1, то функция обладает теми же свойствами, что и y = x3. y = x3; y = x5

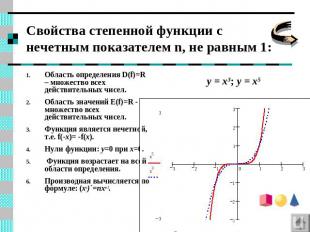
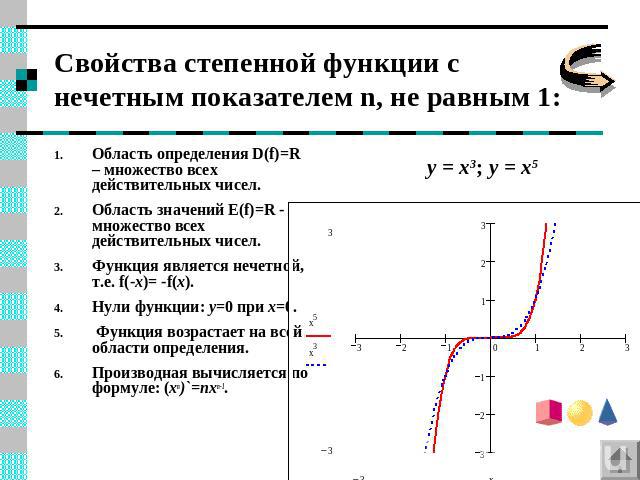
Свойства степенной функции с нечетным показателем n, не равным 1: y = x3; y = x5 Область определения D(f)=R – множество всех действительных чисел.Область значений E(f)=R - множество всех действительных чисел.Функция является нечетной, т.е. f(-x)= -f(x).Нули функции: y=0 при x=0. Функция возрастает на всей области определения.Производная вычисляется по формуле: (xn)`=nxn-1.

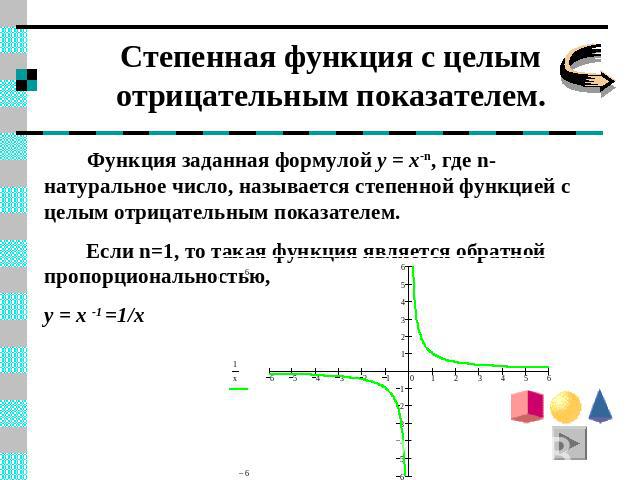
Степенная функция с целым отрицательным показателем. Функция заданная формулой y = x-n, где n- натуральное число, называется степенной функцией с целым отрицательным показателем. Если n=1, то такая функция является обратной пропорциональностью, y = x -1 =1/x

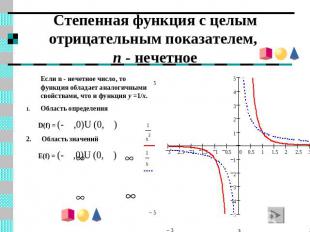
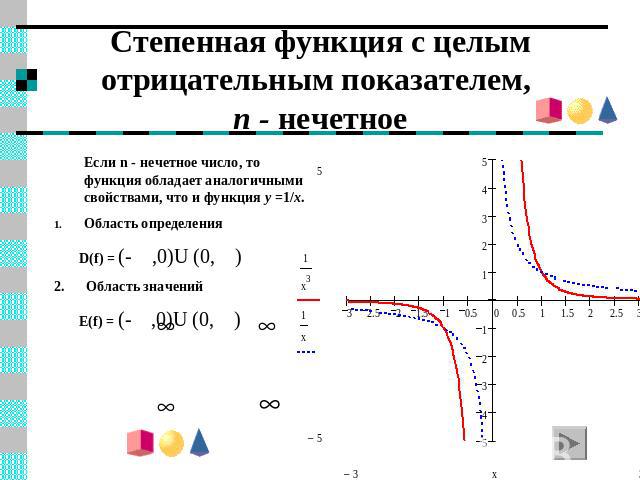
Степенная функция с целым отрицательным показателем, n - нечетное Если n - нечетное число, то функция обладает аналогичными свойствами, что и функция y =1/x.Область определения D(f) = (- ,0)U (0, )2. Область значений E(f) = (- ,0)U (0, )

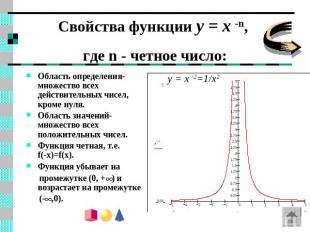
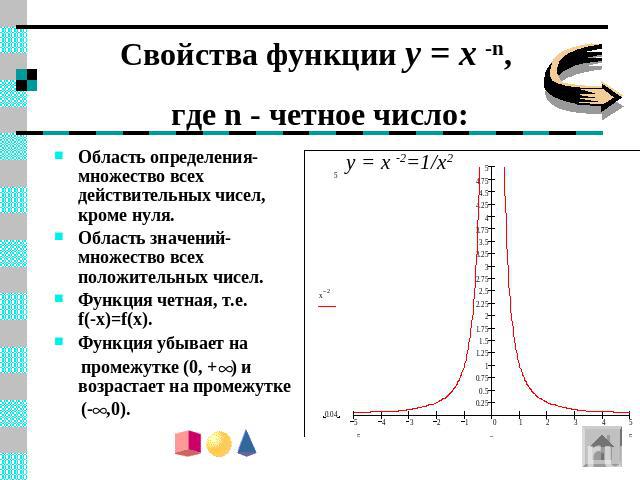
Свойства функции y = x -n, где n - четное число: Область определения- множество всех действительных чисел, кроме нуля.Область значений- множество всех положительных чисел.Функция четная, т.е. f(-x)=f(x). Функция убывает на промежутке (0, + ) и возрастает на промежутке (- ,0). y = x -2=1/x2

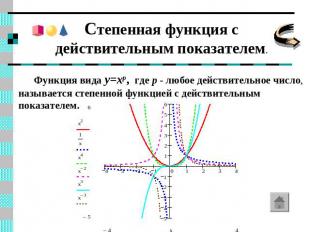
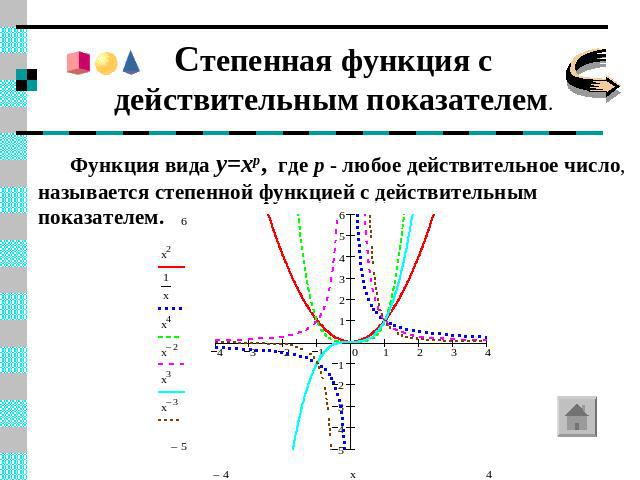
Степенная функция с действительным показателем. Функция вида y=xp, где p - любое действительное число, называется степенной функцией с действительным показателем.

Литература. Дадаян А.А. Математика: Учебник.-М.:ФОРУМ: ИНФРА-М, 2006Математика.Справочник школьника.Филологическое общество «Слово».Москва 1995.3. Программное обеспечение : MS PowerPoint, MS Microsoft Word, математический пакет Mathcad.