Презентация на тему: Самоучитель решения неравенств первой и второй степени с параметрами при определенном условии

Самоучитель решения неравенств первой и второй степени с параметрами при определенном условии Работу выполнилученик 11 класса Афанасьев Алексей

От автора. Это небольшое пособие хочу предложить ребятам одиннадцатиклассникам для того, чтобы разобраться с решением неравенств с параметрами при определенном условии, упорядочить свои знания . Данная тема считается довольно сложной. Ее изучение идет на элективных курсах. Но ребятам, кто не может по каким – то причинам посещать эти курсы и считает себя достаточно сильным, чтобы разобраться в этой теме самим , я предлагаю мое пособие. Здесь представлен алгоритм решения таких заданий и методические рекомендации по их выполнению». Рекомендую всем 11-классникам прочитать это пособие. Оно поможет вам разобраться с данным материалом, сэкономить свое время и проверить свои знания по данной теме. Вместе с пособием прилагаются электронные тесты.

При подготовке к ЕГЭ становится необходимостью изучать некоторые темы раздела курса «Алгебры и начала анализа» самостоятельно, так как в школьном курсе их не изучают вообще или затрагивают вскольз.Данная работа предназначена для самостоятельного изучения учащимися темы «решения неравенств первой и второй степени с параметрами при определенном условии »Работа написана на основе анализа материалов ЕГЭ по математике за последние годы. Данная тема содержит ключевые моменты теории (определения, основные понятия, формулы и. т. д. ), описание методики решения типичных задач и некоторое количество подробно разобранных примеров.Нельзя дать универсальных указаний по решению задач с параметрами. Но для неравенств первой и второй степени с параметрами при заданном условии можно рекомендовать использовать графический метод решения, как более наглядный. При этом можно наглядно рассмотреть задачи, включающие несколько возможных случаев. Данный способ решения можно считать универсальным, так как он подходит для всех заданий такого типа.В самоучителе представлен алгоритм решения заданий для того , чтобы наиболее четко видеть «путь» решения. К пособию прилагаются тесты с электронной обработкой, созданные в программе Ехcеl . Афанасьев Алексей

Оглавление От автораИсходные понятия. Решение неравенств 1 степени с параметрами при определенном условииРешение неравенств 2 степени с параметрами при определенном условииДемонстрационные тесты.

Как понять «неравенства с параметрами» ??? Исходные понятия Истина не передается-она добивается. В.Ф. Одоевский

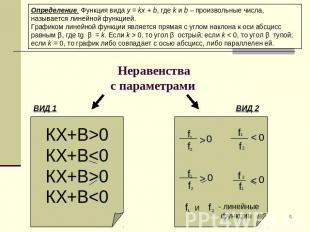
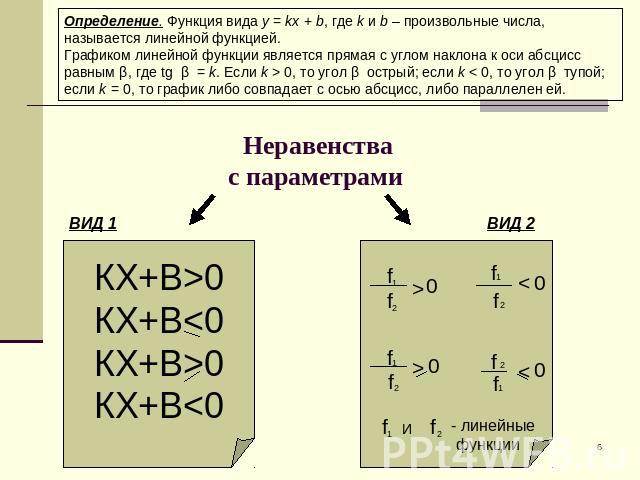
Определение. Функция вида y = kx + b, где k и b – произвольные числа, называется линейной функцией.Графиком линейной функции является прямая с углом наклона к оси абсцисс равным β, где tg  β = k. Если k > 0, то угол β острый; если k < 0, то угол β тупой; если k = 0, то график либо совпадает с осью абсцисс, либо параллелен ей. Неравенствас параметрами КХ+В>0КХ+В<0КХ+В>0КХ+В<0 - линейные функции

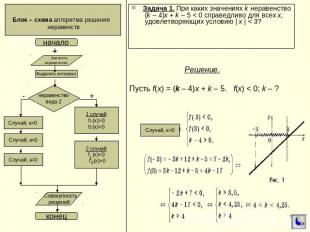
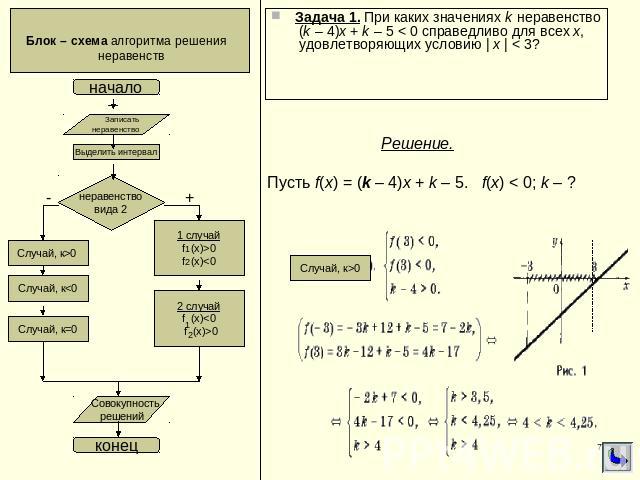
Блок – схема алгоритма решения неравенств Задача 1. При каких значениях k неравенство (k – 4)x + k – 5 < 0 справедливо для всех x, удовлетворяющих условию | x | < 3? Решение. Пусть f(x) = (k – 4)x + k – 5. f(x) < 0; k – ?

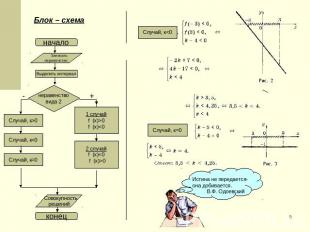
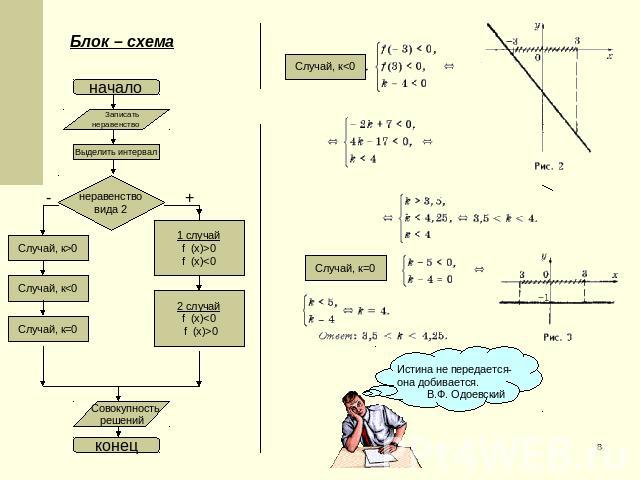
Блок – схема Случай, к<0 Случай, к=0 Истина не передается-она добивается. В.Ф. Одоевский

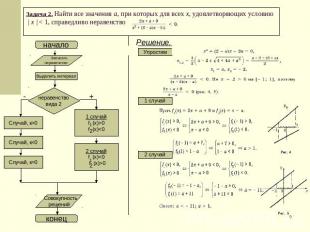
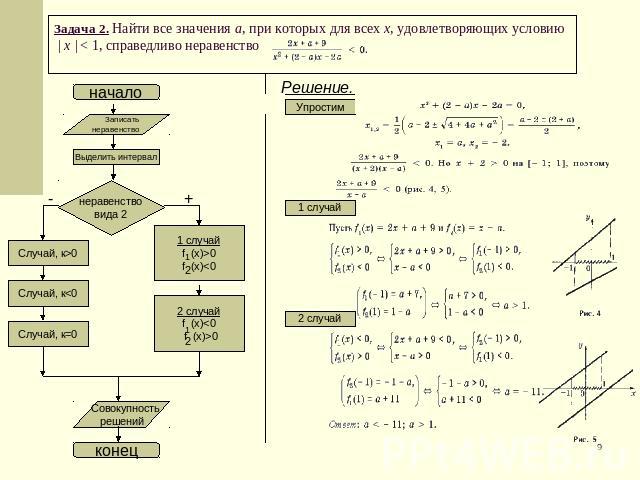
Задача 2. Найти все значения a, при которых для всех x, удовлетворяющих условию | x | < 1, справедливо неравенство Решение.

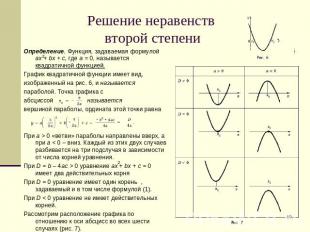
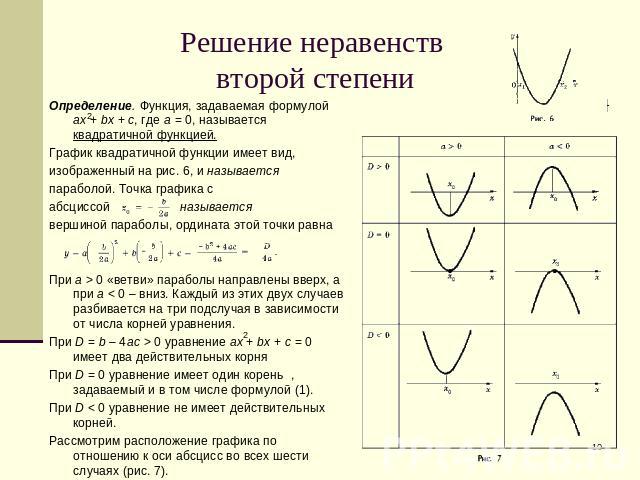
Решение неравенств второй степени Определение. Функция, задаваемая формулой ax + bx + c, где a = 0, называется квадратичной функцией.График квадратичной функции имеет вид,изображенный на рис. 6, и называетсяпараболой. Точка графика сабсциссой   называется вершиной параболы, ордината этой точки равна При a > 0 «ветви» параболы направлены вверх, а при a < 0 – вниз. Каждый из этих двух случаев разбивается на три подслучая в зависимости от числа корней уравнения.При D = b – 4ac > 0 уравнение ax + bx + c = 0 имеет два действительных корняПри D = 0 уравнение имеет один корень  , задаваемый и в том числе формулой (1).При D < 0 уравнение не имеет действительных корней. Рассмотрим расположение графика по отношению к оси абсцисс во всех шести случаях (рис. 7).

Алгоритм решения неравенств второй степени( в частности см. задачу 1) Записать неравенствоВыделить интервал, на котором будет рассматриваться решение данного неравенстваВычислить дискриминант, значение функции на концах интервала ( т.е. D, f(-2), f(1) см. задачу 1)Рассмотреть всевозможные случаи расположения графиков для данного неравенства ( случаев может быть разное количество)Составить систему неравенств для каждого случая, для этого рассмотреть : 1) коэффициент перед х ( в данном случае m , см. задачу 1) 2) дискриминант 3) значения функций на концах . . интервала Решить системы неравенствВ итоге записать совокупность решения систем каждого случая Задача 1. При каких значениях m неравенство mx – 2(m + 3)x + m < 0 верно при всех x, удовлетворяющих условию – 2 < x < 1?Решение. Пусть f(x) = mx – 2(m + 3)x + m. Тогда ( х- аргумент для вершины параболы)

Рубрика«Вопрос – ответ» Вопрос. Какую нужнопреследовать цель при изучении решения неравенств второй степени ?Ответ. Изучить основные приемы решения.Выработать умениянахождения приемов решенияпри решении неравенств смешанных типов. Вопрос. С чего начинатьрассмотрение каждого случаяОтвет. С графическогоизображения. Вопрос . Каково минимальноеколичество случаев, котороеможет быть при рассмотренииданных неравенств?.Ответ. Один случай( см. задачу 2)

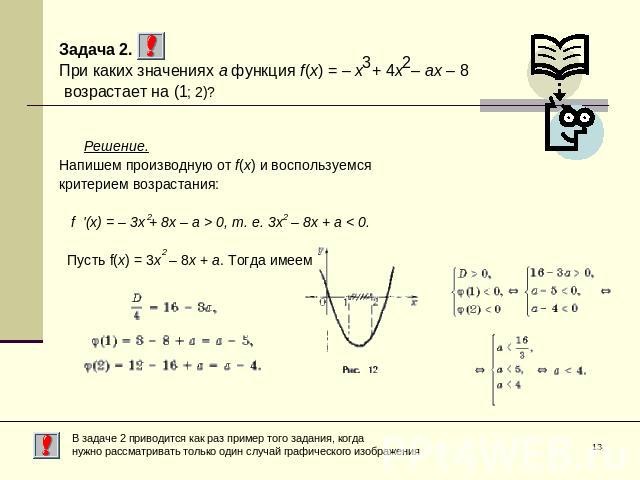
Задача 2. При каких значениях a функция f(x) = – x + 4x – ax – 8 возрастает на (1; 2)? Решение.Напишем производную от f(x) и воспользуемсякритерием возрастания: f  '(x) = – 3x + 8x – a > 0, т. е. 3x – 8x + a < 0. Пусть f(x) = 3x – 8x + a. Тогда имеем В задаче 2 приводится как раз пример того задания, когда нужно рассматривать только один случай графического изображения

Литература Пособие по подготовке. Математика. ЕГЭ. Централизованное тестирование. Санкт-Петербург.2003 г. Пособие по подготовке. Математика. ЕГЭ. Централизованное тестирование. Санкт-Петербург.2004 г. Пособие по подготовке. Математика. ЕГЭ. Централизованное тестирование. Санкт-Петербург.2007 г. Пособие по подготовке. Математика. ЕГЭ. Централизованное тестирование. Санкт-Петербург.2008 г. Пособие по подготовке. Математика. ЕГЭ. Централизованное тестирование. Санкт-Петербург.2008 г. Репетитор по математике. А.И. Замыслова.Задачи вступительных экзаменов по математике. В.С. Белоносов. Повторяем и систематизируем школьный курс алгебры и начал анализа. В.С. Крамор.1С-репетитор по математике .ЕГЭ .(Диск СD-R)