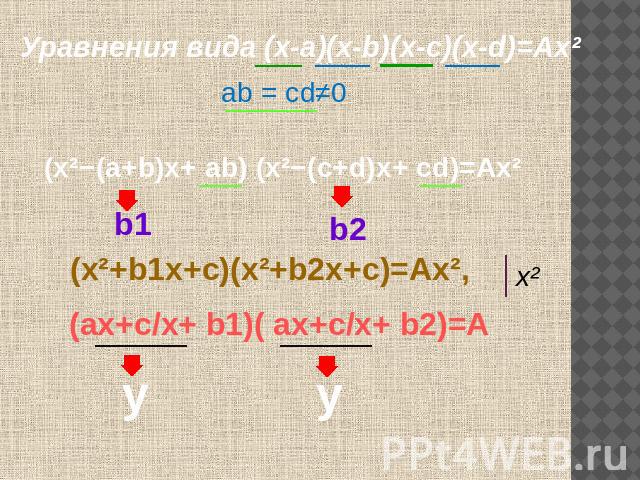Презентация на тему: Решение уравнений n-й степени, n>2. Нахождение корней многочленов

Решение уравнений n-й степени, n>2. Нахождение корней многочленов Выполнила: Адаменко ЛадаПроверила: Мякинникова О.Б.

Уравнение вида а nх n +а n–1х n–1+…+а¹х+аº=0называется алгебраическим уравнением n-й степени

Пусть несократимая дробь р/ q является корнем многочлена n-й степени P(х)= а nх n +а n–1х n–1+…+а¹х+аº с цельными коэффициентами. Тогда число р является делителем свободного члена а , а q – делителем старшего коэффициента а nх n +а n–1х n–1+ …+а¹х+аº q - делитель Р - делитель

Если число а – корень многочлена Р(х), то Р(х) делится на (х – а) без остатка

Решить уравнение: х4+х³+3х²-5х =0 Делители свободного члена ±1,±2 Делители старшего коэффициента ±1, ±3 ± 1, ±2, ±⅓, ±⅔. Возможные корни уравнения 3* х4+ х³+3* х²−5* х−2=0 3*1+1+3*1 – 5*1 – 2 =0 0=0

3х4+х³+3х²-5х-2 3х4-3х³ 4х³+3х² 7х²-5х 7х²-7х 2х-2

3 х³+4х²+7х+2 3 х³+х² 3х²+7х 3х²+х 6х+2 Возможные корни: ±1, ±⅔, ±⅓, ±2- ⅓ - корень уравнения Ответ: 1, −⅓

Уравнения высоких степеней 1.Метод подбора корня многочлена по его старшему и свободному коэффициентам 2. Метод понижения степени.3. Замена переменных

Решить уравнение (х+1)² (х²+2х)=12 (х²+2х (х²+2х) у²+у=12у²+у–12 =0 х²+2х Корней нет х=1

Уравнения специального вида Уравнения вида (х-а)(х-b)(х-с)(х-d)=А а < b < c < d,b-a=d-с (а+b+с+d)

Решить уравнение(12х–1)(6х –1)(4х – 1)(3х –1)=5 (12х–1)(6х –1)(4х – 1)(3х –1)=5 3*4*6*12

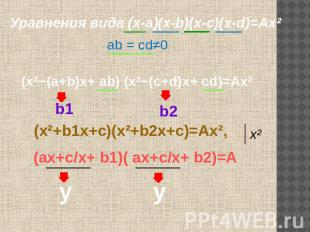
Уравнения вида (х-а)(х-b)(х-с)(х-d)=Ах² аb = сd≠0 (х²−(а+b)х+ аb) (х²−(с+d)х+ сd)=Ах² (х²+b1х+с)(х²+b2х+с)=Ax², (ах+с/х+ b1)( ах+с/х+ b2)=А

Решить уравнение(х+2)(х+3)(х+8)(х+12)=4х² (х²+14х+24)(х²+11х+24)= 4х².

Используемая литература: Энциклопедия для детей. Математика. М.Аксенова Новый справочник школьника. Математика. 1С: Репетитор. Математика. Алгебраические уравнения и неравенства. А. И. Азаров.